M O D E L L I D I F F E R E N Z I A L I
(vedi qui per una versione aggiornata)
(1) L'equazione D(f)(x) = Derf(x) viene detta equazione differenziale in quanto in essa compare il simbolo di derivata.
D(f)(x) = Derf(x) AND f(x0)=y0 è vera se la funzione f che ha Derf come derivata e ha grafico passante per (x0,y0).
In questo caso, le soluzioni dell'equazione differenziale D(f)(x) = Derf(x) non sono altro che
l'integrale indefinito
Più in generale possiamo studiare problemi del tipo D(f)(x) = g(x,f(x)) AND f(x0)=y0 in cui la derivata di f in x dipende non solo da x ma anche dal valore f(x).
Spesso la funzione incognita viene indicata x -> y(x). Si ottiene allora la formulazione:
y'(x) = g(x,y(x)) AND y(x0)=y0, spesso abbreviata in:
y' = g(x,y) AND y(x0)=y0
Vedi gli appunti di Calculus per approfondimenti. Vediamo un esempio.
(2) Un recipiente contiene 100 litri di una soluzione contenente 5 kg di sali.
Viene fatta entrare, con la portata di 1 litro/min, un'altra soluzione con una concentrazione di sali di 10 g/litro.
Il livello e' mantenuto costante mediante un'opportuna valvola.
Supponiamo che la portata sia costante e che il liquido sia costantemente mescolato.
Quanto sale rimane nel recipiente dopo un'ora?
Consideriamo:
# Sale(t): sale in kg presente al minuto t-esimo
# Sale(t)/100: concentrazione di sale all'istante t
# Flusso di sale in entrata: 10 g/litro * 1 litro/min = 10 g/min = 0.01 kg/min
# Flusso di sale in uscita: Sale(t)/100 kg/litro * 1 litro/min = Sale(t)/100 kg/min
Sale(0)=5; D(Sale)(t) = 0.01 - Sale(t)/100
Questo e' il MODELLO DIFFERNZIALE del fenomeno.
In questo caso siamo di fronte a una equazione del tipo y' = g(y), in cui non compare la x ma solo la y.
(3) Proviamo a risolvere il modello con tecniche simboliche.
Potremmo farlo a mano separando le variabili (vedi), ma facciamo fare i conti a Maple (comando dsolve):
Potremmo usare anche il gratuito http://www.WolframAlpha.com,
introducendo:
y'-0.01+y/100 = 0, y(0)=5
| > | dsolve(diff(Sale(t),t) = 0.01-Sale(t)/100,Sale(t)); |
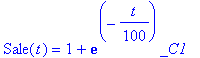
_C1 e' il parametro al variare del quale ho le soluzioni
sostituisco t=0 e Sale(0)=5
| > | subs(t=0,Sale(0)=5,dsolve(diff(Sale(t),t)= 0.01-Sale(t)/100,Sale(t))); |
5 = 1 + e0 _C1
| > | solve(",_C1); [o con % al posto di "] |
![]()
# A questo punto metto t=60 e _C1=4 e ottengo:
| > | subs(_C1=4,dsolve(diff(Sale(t),t)= 0.01-Sale(t)/100,Sale(t))); subs(t=60,_C1=4,dsolve(diff(Sale(t),t)= 0.01-Sale(t)/100,Sale(t))); evalf(subs(t=60,_C1=4,dsolve(diff(Sale(t),t)= 0.01-Sale(t)/100,Sale(t)))); |
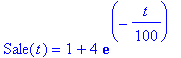
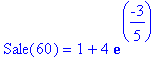
![]()
Volendo posso mettere direttamente le condizioni iniziali nel comando dsolve:
| > | dsolve({diff(Sale(t),t) = 0.01-Sale(t)/100,Sale(0)=5},Sale(t)); |
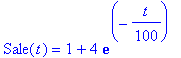
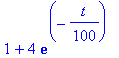
Qui Maple ha trovato la soluzione dell'equazioni, non ha definito Sale(.) come funzione. Non posso battere Sale(60) e ottenere il risultato. Posso fare in due modi:
## sostituire 60 a t, come gia' fatto sopra:
| > | evalf(subs(t=60,dsolve({diff(Sale(t),t) = 0.01-Sale(t)/100,Sale(0)=5},Sale(t)))); |
![]()
## Definire una funzione x->Sal(x) copiando col mouse la parte a destra di Sale(t):
| > | Sal:=t->1+4*exp(-1/100*t); |
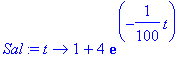
Invece di fare questa cosa a mano, potrei estrarre con il comando op il secondo termine di Sale(t)= ...:
| > | Sal:=t-> op(2, dsolve({diff(Sale(t),t) = 0.01-Sale(t)/100,Sale(0)=5},Sale(t)) ); |
![]()
| > | Sal(t); # ecco il valore di Sal(t): |
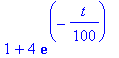
| > | evalf(Sal(60)); |
![]()
---------------------------------------------------------
#Circuito RL L*D(ic)(t)+R*ic-V(t)=0 (L induttanza in Henry, R resistenza in Hom, ic intensita' corrente in Ampere, V tensione in Volt)
# L=1, R=2, V(t)=6, i0=3, i0=2, i0=4; V(t)=6*cos(2t), i0=0, i0=2
| > | L:=1: R:=2: V:= t -> 6: i0:=3: 'L*diff(ic(t),t)+R*ic(t)=V(t)'; dsolve({L*diff(ic(t),t)+R*ic(t)=V(t), ic(0)=i0}, ic(t)); plot (op(2,%),t=0..10,-1..4); [o " al posto di %] |
![]()
![]()
![[Maple Plot]](200506/moddif/moddif54.gif)
Per i0=3 (ossia y0=3) si e' a regime costante: la derivata in 0 risulta essere -2*3+6 = 0. Proviamo con i0=2
| > | L:=1: R:=2: V:= t -> 6: i0:=2: dsolve({L*diff(ic(t),t)+R*ic(t)=V(t), ic(0)=i0}, ic(t)); plot (op(2,%),t=0..10,-1..4); [o " al posto di %] |
![]()
![[Maple Plot]](200506/moddif/moddif56.gif)
Asintoticamente tende a 3. Cambiamo V:
| > | L:=1: R:=2: V:= t-> 6*cos(2*t): i0:=0: dsolve( {L*diff(ic(t),t)+R*ic(t)=V(t), ic(0)=i0}, ic(t)); plot (op(2,%),t=0..20,-3..3); [o " al posto di %] |
![]()
![[Maple Plot]](200506/moddif/moddif58.gif)
| > | L:=1: R:=2: V:= t-> 6*cos(2*t): i0:=2.5: dsolve( {L*diff(ic(t),t)+R*ic(t)=V(t), ic(0)=i0}, ic(t)); plot (op(2,%),t=0..20,-3..3); [o " al posto di %] |
![]()
![[Maple Plot]](200506/moddif/moddif60.gif)
Indipendentemente dal valore iniziale il fenomeno tende ad essere periodico, con lo stesso periodo di V. Si puo' verificare (variando anche L) che tale curva ha uno sfasamento rispetto a quello della tensione che cresce con L.
-----------------------------------------------------
In una reazione chimica i reagenti R1 e R2 combinano due loro singole molecole formando una molecola del prodotto P. La velocita' della reazione e' proporzionale secondo un fattore K al prodotto delle concentrazioni di R1 e R2. Siano C1 e C2 le concentrazioni iniziali (in molecole/cm^3) di, rispettivamente, R1 e R2. Vogliamo esprimere in funzione del tempo t la concentrazione C di P
| > | dsolve({diff(C(t),t) = K*(C1-C(t))*(C2-C(t)),C(0)=0},C(t)); |
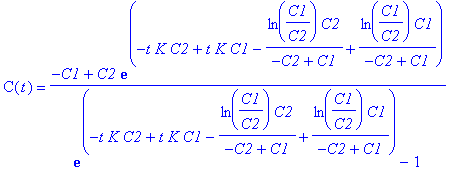
| > | simplify(dsolve({diff(C(t),t) = K*(C1-C(t))*(C2-C(t)),C(0)=0},C(t))); |
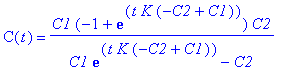
| > | # Provare a risolverla nel caso in cui C1=..., C2= ... e a tracciarne i grafici |
-------------------------------------------------------------
Esercizio. Risolvere con Maple le equazioni differenziali del primo ordine considerate nelle dispense di Calculus e confronatare le soluzioni ottenute con le soluzioni e i grafici presentati nelle dispense.
-------------------------------------------------------------
(4) Il tracciamento del campo direzionale consente di individuare facilmente i casi critici in cui non esiste un'unica soluzione, oltre che avere un'idea di come, al variare delle condizioni inziali, varia la forma delle soluzioni.
La seguente PROCEDURA (sottoprogramma), che useremo a scatola nera, permette di tracciare il CAMPO delle DIREZIONI delle soluzioni di una equazione differenziale del primo ordine. Prova a usarlo per riottenere quelli tracciati nelle dispense di Calculus.
| > | CampoDir := proc(f,xsin,xdes,ygiu,ysu) local Df, Nx, Ny, hx, hy, i, x, y, A, j, rap, T: Df:=(x,y)->f(x,y): Nx:=22 : Ny:=15: hx:=(xdes-xsin)/Nx: hy:=(ysu-ygiu)/Ny: for i from 1 to Nx do x[i]:=xsin+hx*(i-.5) od : for i from 1 to Ny do y[i]:=ygiu+hy*(i-.5) od: A := array(1..Nx*Ny):for i from 1 to Nx do for j from 1 to Ny do if abs(Df(x[i],y[j]))>abs(hy) then rap:= hy/(Df(x[i],y[j])*hx) else rap:=1 fi: rap:=rap*0.7: A[i+Nx*(j-1)] :=[[x[i]-hx/2*rap,y[j]-Df(x[i],y[j])*hx/2*rap],[x[i]+hx/2*rap,y[j]+Df(x[i],y[j])*hx/2*rap]] od od: T:=convert(A,list): plot(T ,color=blue,scaling=constrained) end: |
Se copi e incolli le righe precedenti in un folgio di Mapple e poi definisci una funzione (con nome f o un altro) e richiami la procedure nel modo seguente, ottieni il campo direzionale.
Ecco il campo direzionale di y'(x) = 1+x/(y(x)^2+1):
| > | f:=(x,y)->1+x/(y^2+1) : CampoDir(f,-8,4,-4,4); |
![[Maple Plot]](200506/moddif/moddif63.gif)
-----------------------------------------------------------------------
(5) Equazione differenziale del secondo ordine. Esempio: moto con accelerazione costante = 10 (m/s^2).
Voglio usare x(t). Ho gia' usato x(). Cancello le assegnazioni gia' fatte.
| > | x := 'x'; |
![]()
| > | diff(x(t),t,t)=10; |
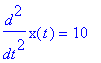
| > | dsolve(diff(x(t),t,t)=10,x(t)); |
![]()
Ora ho due parametri da cui dipende la soluzione. Posso ad es. fissare la velocita' e la posizione in un dato istante, ad es. porre che all'istante 2 la velocita' sia 5 e la posizione sia 3. Posso trovare c1 e c2 sostituendo e risolvendo il sistema ottenuto. Oppure direttamente con Maple:
| > | dsolve({diff(x(t),t,t)=10, x(2)=3, D(x)(2)=5},x(t)); |
![]()
x=tempo, y= posizione di oggetto di massa M sottoposto a una forza di -K*y (ad es. esercitata da una molla) con K/M =4 e a una una
da F=-k*y(t), F=m*y"(t) ho:
| > | y:='y': diff(y(x),x,x) = - k/m*y(x); |
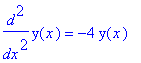
| > | k:=4: m:=1: dsolve(diff(y(x),x,x) = - k/m*y(x),y(x)); |
![]()
Inseirisco una posizione inziale e una velocita' iniziale
| > | dsolve({ diff(y(x),x,x) = - k/m*y(x), y(0)=2, D(y)(0)=0}, y(x)); plot (op(2,%),x=0..10,-2..2); [o " al posto di %] |
![]()
![[Maple Plot]](200506/moddif/moddif71.gif)
y" = -(k/m)*y + F/m*cos(omega*t) (oscillazioni forzate, con forza oscillante esterna, del tipo F*cos(omega*t)
F=2, omega=0.5
| > | dsolve({ diff(y(x),x,x) = - k/m*y(x) + 2*cos(0.5*x), y(0)=2, D(y)(0)=0}, y(x)); plot (op(2,%),x=0..40,-2..2); [o " al posto di %] |
![]()
![[Maple Plot]](200506/moddif/moddif73.gif)
F=1, omega=2 - risonanza
| > | dsolve({ diff(y(x),x,x) = - k/m*y(x) + cos(2*x), y(0)=2, D(y)(0)=0}, y(x)); plot (op(2,%),x=0..40); [o " al posto di %] |
![]()
![[Maple Plot]](200506/moddif/moddif75.gif)
y" = -(k/m)*y - k1*y' (oscillazioni smorzate, con forza attrito proporzionale a velocita'
con k1:=1
| > | dsolve({ diff(y(x),x,x) = - k/m*y(x) - diff(y(x),x), y(0)=2, D(y)(0)=0}, y(x)); plot (op(2,%),x=0..10); [o " al posto di %] |
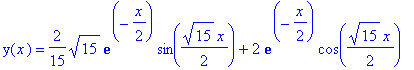
![[Maple Plot]](200506/moddif/moddif77.gif)
con k1:=10 (non ci sono neanche oscillazioni):
| > | dsolve({ diff(y(x),x,x) = - k/m*y(x) - 10*diff(y(x),x), y(0)=2, D(y)(0)=0}, y(x)); plot (op(2,%),x=0..10); [o " al posto di %] |
![]()
![[Maple Plot]](200506/moddif/moddif79.gif)
Traccio anche la curva (y(x),y'(x)) che rappresenta la relazione tra y e la sua velocita' (diagramma di fase). In questo caso ottengo una ellisse. Il fatto che sia una curva chiusa e' legato al fatto che la soluzione è periodica.
| > | diff(y(x),x,x) = - k/m*y(x); dsolve({ %, y(0)=2, D(y)(0)=0}, y(x)); yx := op(2,%): plot (yx,x=0..10,-2..2); plot ([yx,diff(yx,x),x=0..10]); [o " al posto di %] |
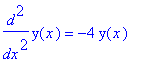
![]()
![[Maple Plot]](200506/moddif/moddif82.gif)
![[Maple Plot]](200506/moddif/moddif83.gif)
Nel caso dello smorzamento:
| > | diff(y(x),x,x) = - k/m*y(x) - diff(y(x),x); dsolve({ %, y(0)=2, D(y)(0)=0}, y(x)); yx := op(2,%): plot (yx,x=0..20,-2..2); plot ([yx,diff(yx,x),x=0..20]); [o " al posto di %] |
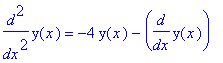
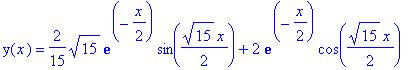
![[Maple Plot]](200506/moddif/moddif86.gif)
![[Maple Plot]](200506/moddif/moddif87.gif)
Nel caso della risonanza:
| > | diff(y(x),x,x) = - k/m*y(x) + cos(2*x); dsolve({ %, y(0)=2, D(y)(0)=0}, y(x)); yx := op(2,%): plot (yx,x=0..20); plot ([yx,diff(yx,x),x=0..20]); [o " al posto di %] |
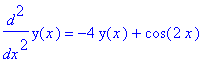
![]()
![[Maple Plot]](200506/moddif/moddif90.gif)
![[Maple Plot]](200506/moddif/moddif91.gif)
----------------------------------------------
(6) EQUAZIONI A DERIVATE PARZIALI
Le equazione differenziali a derivate parziali (ossia che coinvolgono le derivate parziali della funzione incognita rispetto a piu' di una variabile), a differenza di quelle ordinarie, hanno soluzioni che non dipendono da costanti arbitrarie ma da funzioni arbitrarie.
Vediamo un primo es. di eq. a derivate parziali (l'incognita e' f):
[facciamo un restart per annullare precedenti assegnazioni]
| > | restart: D[2](f(x,y))=x; |
![]()
che puo' essere scritta anche:
| > | diff(f(x,y),y)=x; |
![]()
Siamo in grado di risoverla direttamente: la derivata rispetto a y di z e' x se z e' del tipo x*y; ma si puo' addizionare un qualunque termine che non contenga y, in quanto la sua derivata rispetto a y e' zero. Quindi le soluzioni sono del tipo: x*y+g(x) con g(x) funzione arbitraria.
Verifichiamo la cosa con Maple; il comando e', a seconda delle versioni di Maple, pdesolve o pdsolve (ParzialDiffentialEquation):
| > | pdsolve(diff(f(x,y),y)=x,f(x,y)); |
![]()
OK. Altro es.
| > | diff(f(x,y),y,y)=x; |
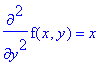
x*y^2/2 e' evidentemente una soluzione. Ma lo rimane se si aggiunge qualcosa che derivato due volte rispetto a y da' 0:
x*y^2 + g(x) + h(x)*y. Verifichiamolo con Maple:
| > | pdsolve(diff(f(x,y),y,y)=x,f(x,y)); |
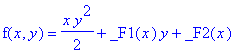
OK.
Risolvi ("ragionando", e poi con Maple):
| > | diff(f(x,y),x,y)=0;pdsolve(diff(f(x,y),x,y)=0,f(x,y)); |
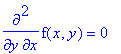
![]()
Ci soffermeremo su solo alcune eq. differenziali a derivate parziali del secondo ordine che si impiegano spesso per modellizzare fenomeni di tipo fisico e tecnologico.
| > | diff(f(x,y),x,x)+diff(f(x,y),y,y)=0; |
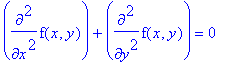
E' la cosiddetta EQUAZIONE DI LAPLACE (o DEL POTENZIALE) in 2 dimensioni. Una funzione (continua con le sue derivate prime e seconde) che la soddisfa viene chiamata "armonica" (la cosa è legata a collegamenti con le serie di Fourier che non esploriamo). Proviamo a trovarne qualcuna: un'idea puo' essere quella di far entrare la funzione esponenziale (che ha se' stessa come derivata) e le funzioni seno e coseno (che hanno il proprio opposto come derivata seconda). In particolare proviamo con (x,y) -> e^(kx)*cos(ky):
| > | g:=(x,y) -> exp(k*x)*cos(k*y); |
![]()
| > | diff(g(x,y),x,x)+diff(g(x,y),y,y); |
![]()
OK. Proviamo anche con:
| > | g:=(x,y) -> exp(k*x)*sin(k*y); |
![]()
| > | diff(g(x,y),x,x)+diff(g(x,y),y,y); |
![]()
OK.
ESERCIZIO. Verificare con Maple che sono armoniche nelle regioni piane indicate:
| > | g:=(x,y) -> 3*x^2*y-y^3; #nel piano |
![]()
| > | g:=(x,y) -> h*(x^2-y^2)+k*x*y; #nel piano |
![]()
| > | g:=(x,y) -> x/(x^2+y^2); # in (x,y)<>(0,0) |
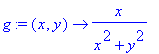
| > | g:=(x,y) -> log(x^2+y^2); # in (x,y)<>(0,0) |
![]()
Risolviamo con Maple:
| > | pdsolve(diff(f(x,y),x,x)+diff(f(x,y),y,y)=0,f(x,y)); |
![]()
Facciamo delle prove (in modo che sparisca l'unità immaginaria) per vedere alcune soluzioni:
| > | a:=x->x^2: b:=x->x^2: g:=(x,y)->a(y+I*x)+b(y-I*x); g(x,y)=simplify(g(x,y)); |
![]()
![]()
| > | a:=x->x^2+I*x: b:=x->x^2-I*x: g:=(x,y)->a(y+I*x)+b(y-I*x); g(x,y)=simplify(g(x,y)); |
![]()
![]()
| > | a:=x->exp(x): b:=x->exp(x): g:=(x,y)->a(y+I*x)+b(y-I*x); g(x,y)=simplify(g(x,y)); |
![]()
![]()
La semplificazione è stata ottenuta usando la formula di Eulero che lega l'esponenziale e le funzioni circolari nel campo complesso:
![]() =
= 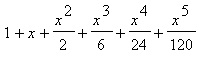 +... sostituendo I*x a x:
+... sostituendo I*x a x: 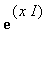 =
= 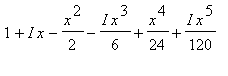 + ...= (
+ ...= (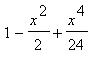 + ...) + I(
+ ...) + I(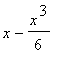 + ...) = cos(x) + I sin(x)
+ ...) = cos(x) + I sin(x)
Infatti da questa relazione ho: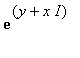 = exp(y)*exp(xI) = exp(y)*(cos(x)+I sin(x))
= exp(y)*exp(xI) = exp(y)*(cos(x)+I sin(x))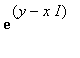 = exp(y)*exp(-xI) = exp(y)*(cos(x)+I sin(-x)) = exp(y)*(cos(x) - I sin(x))
= exp(y)*exp(-xI) = exp(y)*(cos(x)+I sin(-x)) = exp(y)*(cos(x) - I sin(x))
da cui, sommando: 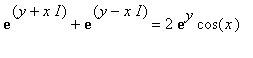
Le armoniche hanno la caratteristica di assumere valori massimo e minimo solo sul contorno del loro dominio; inoltre se si annullano sul contorno del dominio allora si annullano in tutto il dominio.
La seguente equazione e' detta EQUAZIONE DELLE ONDE (in una dimensione).
| > | diff(f(x,t),t,t)=k^2*diff(f(x,t),x,x); |
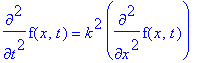
| > | pdsolve(diff(f(x,t),t,t)=k^2*diff(f(x,t),x,x),f(x,t)); |
![]()
E' facile verificare direttamente che questa (al variare di _F1 e _F2) e' una soluzione.
Se la variabile t indica il tempo, _F2(t*k-x) rappresenta una forma d'onda che si propaga lungo l'asse x con velocita' k; _F1(t*k+x) ne rappresenta una che si sposta verso sinistra.
Quella che segue e' l'EQUAZIONE DEL CALORE (in 1 dimensione). Se f(x,t) e' la temperatura nella posizione x di un'asta all'istante t, l'eq. rappresenta la diffusione del calore in un'asta isolata.
Idea:
un piccolo oggetto posto in un'ambiente a temperatura costante T ha temperatura f(t) che varia con velocita' proporzionale alla differenza di temperatura dall'ambiente:
d f(t) / dt = k(T-f(t)). La soluzione e' una esponenziale negativa.
Nel caso della nostra asta solo un estremo e' a contatto con la sorgente di calore.
| > | diff(f(x,t),t)=diff(f(x,t),x,x); |
| > | pdsolve(diff(f(x,t),t)=diff(f(x,t),x,x),f(x,t)); |
![`&where`(f(x,t) = _F1(x)*_F2(t),[{diff(_F2(t),t) = _c[1]*_F2(t), diff(_F1(x),`$`(x,2)) = _c[1]*_F1(x)}])](200506/moddif/moddif126.gif)
| > | g:=(x,t)->t^(-1/2)*exp(-x^2/(4*t)); # verifichiamo che e' una soluzione |
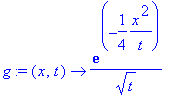
| > | diff(g(x,t),t);diff(g(x,t),x,x); |
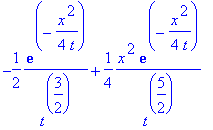
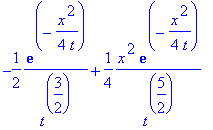
Eq. del calore in 2 dimensioni (diffusione del calore nel piano):
| > | diff(f(x,y,t),t)=diff(f(x,y,t),x,x)+diff(f(x,y,t),y,y); |
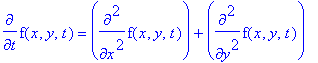
| > | g:=(x,y,t)->t^(-1)*exp(-(x^2+y^2)/(4*t)); # verifica che e' una soluzione |