M O D E L L I D I F F E R E N Z I A L I
del primo ordine
del secondo ordine
alle derivate parziali
Attività con R sulle eq. differenziali del 1º ordine e quelle di ordine superiore.
Vedi anche qui.
(1) L'equazione D(f)(x) = h(x) viene detta
equazione differenziale in quanto in essa compare
il simbolo di derivata.
D(f)(x) = h(x) AND f(x0)=y0 è vera se la funzione f che ha h come derivata e ha grafico
passante per (x0,y0).
In questo caso le soluzioni dell'equazione differenziale
D(f)(x) = h(x) non sono altro che l'integrale indefinito
La condizione f(x0)=y0 individua una particolare f tra tutte le funzioni che hanno h come derivata.
Più in generale possiamo studiare problemi del tipo D(f)(x) = g(x,f(x))
AND f(x0)=y0 in cui la derivata di f in x dipende non solo da x ma anche dal valore f(x).
Spesso la funzione incognita viene indicata x -> y(x). Si ottiene allora la formulazione:
y'(x) = g(x,y(x)) AND y(x0)=y0, spesso abbreviata in:
y' = g(x,y) AND y(x0)=y0
Vedi gli appunti di "Calculus" per approfondimenti. Vediamo un esempio.
(2) Un recipiente
contiene 100 litri di una soluzione contenente 5 kg di sali.
Viene fatta entrare, con la portata di 1 litro/min, un'altra soluzione con una concentrazione di sali di 10 g/litro.
Il livello è mantenuto costante mediante un'opportuna valvola.
Supponiamo che la portata sia costante e
che il liquido sia costantemente mescolato.
Quanto sale rimane nel recipiente dopo un'ora?
Consideriamo:
# Sale(t): sale in kg presente al minuto t-esimo
# Sale(t)/100: concentrazione di sale all'istante t
# Flusso di sale in entrata: 10 g/litro * 1 litro/min = 10 g/min = 0.01 kg/min
# Flusso di sale in uscita: Sale(t)/100 kg/litro * 1 litro/min = Sale(t)/100 kg/min
Sale(0)=5; D(Sale)(t) = 0.01 - Sale(t)/100
Questo è il MODELLO DIFFERNZIALE del fenomeno.
In questo caso siamo di fronte a una equazione del tipo y' = g(y), in cui non compare la x ma solo la y.
(3)
Proviamo a risolvere il modello con tecniche simboliche.
Potremmo farlo a mano separando le variabili (vedi), ma facciamo fare i conti
a WolframAlpha (se vuoi fare i calcoli con Maple
vedi qui), introducendo:
S'(t)-0.01+S(t)/100 = 0, S(0)=5
Otteniamo S(t) = 1 + 4*exp(-0.01*t)
e infine:
1 + 4*exp(-0.01*60) = 3.19524654437610573… Questo è Sale(60) (che arrotondo a 3.20).
---------------------------------------------------------
# Circuito RL L*D(i)(t)+R*i(t)-V(t)=0 (L induttanza in Henry, R resistenza in Hom, i intensità corrente in Ampere,
V tensione in Volt)
# L=1, R=2, V(t)=6, i0=3, i0=2, i0=4; V(t)=6*cos(2t), i0=0, i0=2.5
Indichiamo con f l'intensità della corrente.
Facciamo i conti con WolframAlpha.
1*f'(t)+2*f(t)=6, f(0)=3
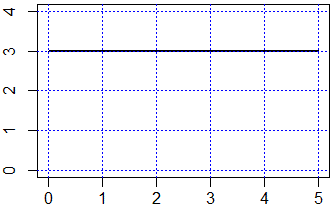
f(t) = 3
Grafico con R:
f <- function(x) 3+x-x; plot(f,0,5,ylim=c(0,4),lwd=2)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)

Per i0=3 si è a regime costante. Proviamo con i0=2
1*f'(t)+2*f(t)=6, f(0)=2
f(t) = 3-exp(-2*t)
Grafico con R f <- function(t) 3-exp(-2*t); plot(f,0,5,ylim=c(0,3),lwd=2) abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
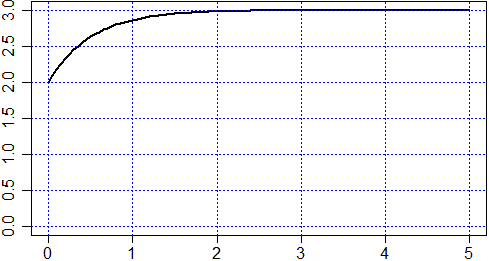
Asintoticamente tende a 3. Cambiamo V:
1*f'(t)+2*f(t)=6*cos(2*t), f(0)=0
f(t) = 3/2*(cos(2*t)+sin(2*t)-exp(-2*t))
f <- function(t) 3/2*(-exp(-2*t)+cos(2*t)+sin(2*t)) plot(f,0,20,lwd=2) abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
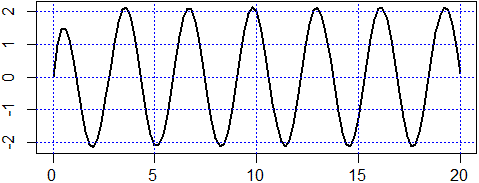
1*f'(t)+2*f(t)=6*cos(2*t), f(0)=2.5
f(t) = exp(-2*t)+1.5*cos(2*t)+3*cos(t)*sin(t)
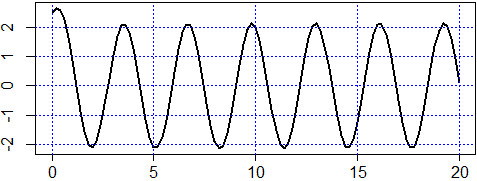
Indipendentemente dal valore iniziale il fenomeno tende ad essere periodico,
con lo stesso periodo di V. Si può verificare (variando anche L) che tale curva ha uno sfasamento rispetto a quello della tensione che cresce con L.
---------------------------------------------------------
In una reazione chimica i reagenti R1 e R2 combinano due loro singole molecole formando una molecola del
prodotto P. La velocità della reazione è proporzionale secondo un fattore K al prodotto delle concentrazioni
di R1 e R2. Siano a e b le concentrazioni iniziali (in molecole/cm^3) di, rispettivamente, R1 e R2.
Vogliamo esprimere in funzione del tempo t la concentrazione C di P
C'(t) = K*(7-C(t))*(3-C(t)), C(0)=0
C(t) = (21*(exp(4*K*t)-1))/(7*exp(4*K*t)-3)
C'(t) = K*(3-C(t))*(5-C(t)), C(0)=0
C(t) = (15*(exp(2*K*t)-1))/(5*exp(2*K*t)-3)
C'(t) = K*(1-C(t))*(1-C(t)), C(0)=0
C(t) = (K*t)/(K*t+1)
C'(t) = K*(a-C(t))*(b-C(t)), C(0)=0
b*(b/a)^(b/(a-b))*exp(a*K*t)-a*(b/a)^(a/(a-b))*exp(b*K*t)
C(t) = —————————————————————————————————————————————————————————
(b/a)^(b/(a-b))*exp(a*K*t)-(b/a)^(a/(a-b))*exp(b*K*t)
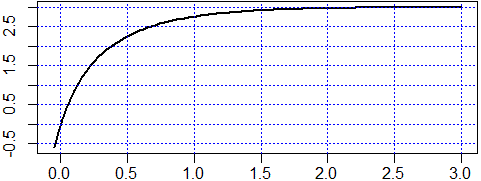
C <- function(t) (21*(exp(4*K*t)-1))/(7*exp(4*K*t)-3); K <- 0.5
plot(C,-0.05,3,lwd=2)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
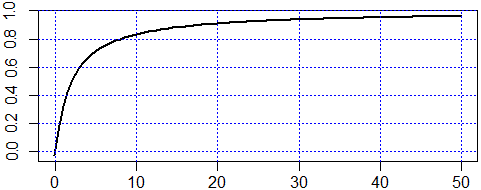
C <- function(t) (K*t)/(K*t+1); K <- 0.5 plot(C,-0.05,50,lwd=2) abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
Esercizio.
Risolvere con WolframAlpha le equazioni differenziali del primo ordine considerate nelle dispense di Calculus
(e farne in grafici con R) e confrontare le soluzioni ottenute con le soluzioni e i grafici presentati
nelle dispense.
-------------------------------------------------------------
(4)
Il tracciamento del campo direzionale consente di individuare facilmente i casi critici in cui non esiste
un'unica soluzione, oltre che avere un'idea di come, al variare delle condizioni inziali, varia la forma
delle soluzioni.
Il seguente algoritmo soledif per R, che useremo a scatola nera, permette di tracciare il
CAMPO delle DIREZIONI delle soluzioni di una equazione differenziale del primo ordine
descritta nella funzione Dy. Incollato, una volta per tutte, in R soledif,
basta via via cambiare Dy e chiamare soledif(...) per ottenere i campi direzionale
di qualunque equazione differenziale del primo ordine. Guarda l'esempio. Quindi prova a
riottenere i campi direzionale tracciati nelle dispense di Calculus.
Ecco il campo direzionale di y'(x) = 1+x/(y(x)^2+1):
# y' = 1+x/(y^2+1)
# Traccio tanti trattini con pendenza 1+x/(y^2+1)
# Ottengo il "campo direzionale" associato alla eq. differenziale.
#
Dy <- function(x,y) 1+x/(y^2+1)
# riduco i margini della pagina
par( mai = c(0.5,0.5,0.2,0.2) )
#
# tracciamento in (x1,x2)*(y1,y2) del campo direzionale di y' = f(x,y)
# con f messo in Dy in righe precedenti; prova con m=25, n=25
# (m e n indicano quanto sono i trattini in orizz. e in vert.)
soledif <- function(x1,x2,y1,y2,m,n) {
plot(c(x1,x2), c(y1,y2), type="n",xlab="",ylab="")
abline(h=0,v=0,col="blue")
dx <- (x2-x1)/m; dy <- (y2-y1)/n
a <- 0; b <- 0; f <- function(x) Dy(a,b)*(x-a)+b
for(i in 0:m) for(j in 0:n) {a <- x1+dx*i; b <- y1+dy*j
Dx <- dx; for(k in 1:100)
{if(abs(f(a+Dx/2.5)-f(a-Dx/2.5)) > dy) Dx <- Dx*0.9 else k <- 100}
plot(f,a-Dx/2.5,a+Dx/2.5,ylim=c(b-dy/2.5,b+dy/2.5),add=TRUE,col="grey55")}}
#
soledif(-8,4,-4,4, 25,25)
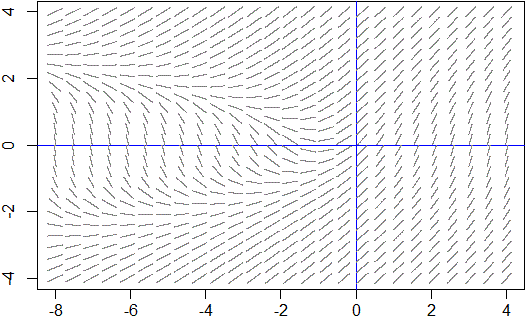
Vedi qui per altri usi di R per risolvere equazioni differenziali.
-----------------------------------------------------------------------
(5) Equazione differenziale del secondo ordine. Esempio: moto con accelerazione costante = 10 (m/s^2).
x''(t) = 10 Ottengo: x(t) = 5*t^2 + c2*t + c1
Ora ho due parametri da cui dipende la soluzione. Posso ad es. fissare la velocità e la posizione in un dato istante, ad es. porre che all'istante 2 la velocità sia 5 e la posizione sia 3. Posso trovare c1 e c2 sostituendo e risolvendo il sistema ottenuto. Oppure direttamente con WolframAlpha:
x''(t) = 10, x(2)=3, x'(2)=5 x(t) = 5*t^2 - 15*t + 13
• x=tempo, y= posizione di oggetto di massa m sottoposto a una forza di -k*y (ad es. esercitata da una molla) con k = 4, m = 1; da F = -k*y(t), F = m*y"(t) ho:
y''(x) = -4/1*y y(x) = c2*sin(2*x)+c1*cos(2*x)Inseirisco una posizione inziale e una velocità iniziale:
y''(x) = -4/1*y, y(0)=2, y'(0)=0 y(x) = 2*cos(2*x)
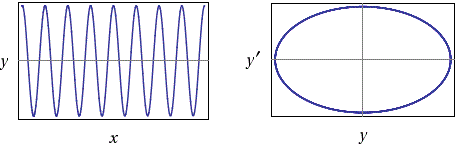
WlframAlpha ha tracciato anche la curva (y(x),y'(x)) che rappresenta la relazione tra y e la sua velocità (diagramma di fase). In questo caso ottengo una ellisse. Il fatto che sia una curva chiusa è legato al fatto che la soluzione è periodica.
• y" = -(k/m)*y + F/m*cos(omega*t) (oscillazioni forzate, con forza oscillante esterna, del tipo F*cos(omega*t)
F=2, omega=0.5
y''(x) = -4/1*y+2*cos(0.5*x), y(0)=2, y'(0)=0 y(x) = 0.533333*cos(0.5*x)+1.46667*cos(2*x) 0.5333... = 8/15 1.4666... = 22/15 y(x) = 8/15*cos(x/2) + 22/15*cos(2*x)
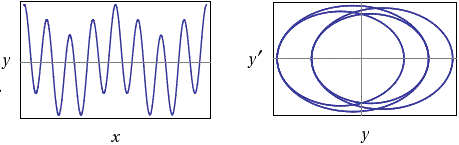
f <- function(x) 8/15*cos(x/2) + 22/15*cos(2*x) plot(f,0,40,n=3000,lwd=2) abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3) dev.new() # apro una nuova finestra per mantenere il graf. precedente fx <- expression( 8/15*cos(x/2) + 22/15*cos(2*x) ) gx <-D(fx,"x"); g <- function(x) eval(gx) x1 <- 0; x2 <- 40; punti <- 3000; x <- seq(x1,x2,(x2-x1)/punti) plot(c(-3,3),c(-4,4),type="n",xlab="", ylab="") abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3) lines(f(x),g(x),lwd=2)
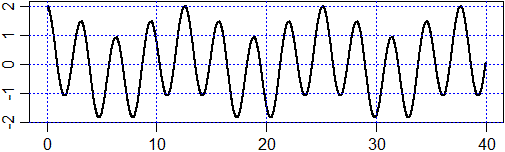
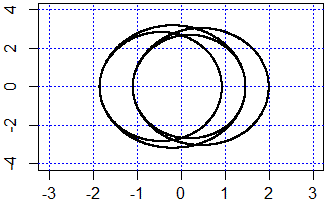
• F=1, omega=2 - risonanza (vedi):
y''(x) = -4/1*y+cos(2*x), y(0)=2, y'(0)=0 y(x) = 2*cos(2*x) + 1/4*x*sin(2*x)
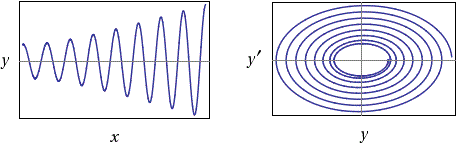
• y" = -(k/m)*y - k1*y' (oscillazioni smorzate, con forza attrito proporzionale a velocità); con k1 = 1:
y''(x) = -4/1*y-y', y(0)=2, y'(0)=0 y(x) = 2/15*exp(-x/2)*(sqrt(15)*sin((sqrt(15)*x)/2) + 15*cos((sqrt(15)*x)/2))
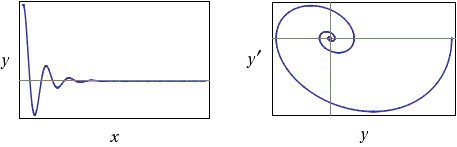
• con k1 = 10 (non ci sono neanche oscillazioni):
y''(x) = -4/1*y-10*y', y(0)=2, y'(0)=0 y(x) = 1/21*exp(-(5+sqrt(21))*x)*((21+5*sqrt(21))*exp(2*sqrt(21)*x)+21-5*sqrt(21))Ecco i grafici (il grafico della soluzione e il diagramma di fase) ottenuti con R:
f <- function(x) 1/21*exp(-(5+sqrt(21))*x)*((21+5*sqrt(21))*exp(2*sqrt(21)*x)+21-5*sqrt(21)) plot(f,0,10,lwd=2) abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
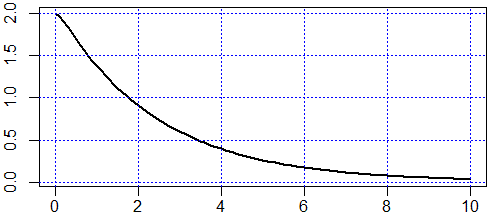
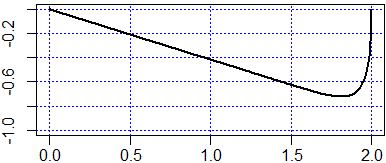
fx <- expression(1/21*exp(-(5+sqrt(21))*x)*((21+5*sqrt(21))*exp(2*sqrt(21)*x)+21-5*sqrt(21))) gx <-D(fx,"x"); f <- function(x) eval(fx); g <- function(x) eval(gx) x1 <- 0; x2 <- 10; punti <- 3000; x <- seq(x1,x2,(x2-x1)/punti) plot(c(0,2),c(-1,0),type="n",xlab="", ylab="") abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3) lines(f(x),g(x),lwd=2)
----------------------------------------------
(6) EQUAZIONI ALLE DERIVATE PARZIALI
Le equazioni differenziali alle derivate parziali (ossia che coinvolgono le derivate parziali della funzione incognita rispetto a piu' di una variabile), a differenza di quelle ordinarie, hanno soluzioni che non dipendono da costanti arbitrarie ma da funzioni arbitrarie.
• Vediamo un primo es. di eq. a derivate parziali (l'incognita è f):
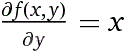
Siamo in grado di risoverla direttamente: la derivata rispetto a y di z è x se z è del tipo x*y;
ma si può addizionare un qualunque termine che non contenga y, in quanto la sua derivata rispetto a y è
zero. Quindi le soluzioni sono del tipo: x*y+g(x) con g(x) funzione arbitraria.
Verifichiamo la cosa con WolframAlpha:
d/dy f(x,y) = x f(x,y) = c1(x) + x*y• OK. Altro esempio.
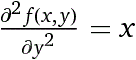
x*y^2/2 è evidentemente una soluzione. Ma lo rimane se si aggiunge qualcosa che derivato due volte rispetto a y dà 0: x*y^2/2 + g(x) + h(x)*y. Verifichiamolo con WolframAlpha:
d^2/dy^2 f(x,y) = x f(x,y) = y*c2(x)+c1(x)+(x*y^2)/2• OK. Risolvi ("ragionando", e poi con WolframAlpha):
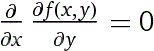
d/dx d/dy f(x,y) = 0 f(x,y) = c1(x)+c2(y)
• Ci soffermeremo su solo alcune eq. differenziali a derivate parziali del secondo ordine che si impiegano spesso per modellizzare fenomeni di tipo fisico e tecnologico.
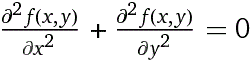
È la cosiddetta EQUAZIONE DI LAPLACE (o DEL POTENZIALE) in 2 dimensioni. Una funzione (continua con le sue derivate prime e seconde) che la soddisfa viene chiamata "armonica" (la cosa è legata a collegamenti con le serie di Fourier che non esploriamo). Proviamo a trovarne qualcuna: un'idea può essere quella di far entrare la funzione esponenziale (che ha sé stessa come derivata) e le funzioni seno e coseno (che hanno il proprio opposto come derivata seconda). In particolare proviamo con (x,y) → exp(kx)*cos(ky); è facile verificare direttamente che:
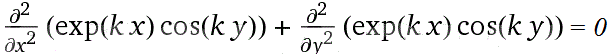
Verifichiamo per questa ed altre funzioni, per far prima, con WolframAlpha:
d^2/dx^2 exp(k*x)*cos(k*y) + d^2/dy^2 exp(k*x)*cos(k*y) = 0 d^2/dx^2 exp(k*x)*sin(k*y) + d^2/dy^2 exp(k*x)*sin(k*y) = 0 d^2/dx^2 (3*x^2*y-y^3) + d^2/dy^2 (3*x^2*y-y^3) = 0 d^2/dx^2 (h*(x^2-y^2)+k*x*y) + d^2/dy^2 (h*(x^2-y^2)+k*x*y) = 0 d^2/dx^2 (x/(x^2+y^2)) + d^2/dy^2 (x/(x^2+y^2)) = 0 [per (x,y) ≠ (0,0)] d^2/dx^2 log(x^2+y^2) + d^2/dy^2 log(x^2+y^2) = 0 [per (x,y) ≠ (0,0)]
Queste sono tutte soluzioni. Proviamo a risolvere in generale l'equazione di partenza, con WolframAlpha, e vediamo che cosa otteniamo:
d^2/dx^2 f(x,y) + d^2/dy^2 f(x,y) = 0 f(x,y) = c1(y+i*x) + c2(y-i*x)Otteniamo il termine c1(y+i*x)+c2(y-i*x) in cui compare l'unità immaginaria i e in cui, in questo caso, c1 e c2 indicano delle generiche funzioni. Quando, semplificando, in tale termine sparisce i, abbiamo una soluzione. Proviamo a vedere la forma di alcune soluzioni, e verifichiamo se esse sono effettivamente tali. Procediamo così:
Metto in WolframAlpha: h=y+i*x, k=y-i*x, h^2+k^2 Ottengo: 2*y^2-2*x^2 Calcolo: d^2/dx^2 (2*y^2-2*x^2) + d^2/dy^2 (2*y^2-2*x^2) = 0 Ottengo: True OK h=y+i*x, k=y-i*x, h^2+i*h+k^2-i*k -2*(x^2+x-y^2) d^2/dx^2 (-2*(x^2+x-y^2)) + d^2/dy^2 (-2*(x^2+x-y^2)) = 0 h=y+i*x, k=y-i*x, exp(h)+exp(k) 2*exp(y)*cos(x) d^2/dx^2 (2*exp(y)*cos(x)) + d^2/dy^2 (2*exp(y)*cos(x)) = 0
La semplificazione è stata ottenuta usando la formula di Eulero che lega l'esponenziale e le funzioni circolari nel
campo complesso:
exp(x) = 1 + x + x^2/2 + x^3/6 + x^4/24 + … Sostituendo i*x a x:
exp(i*x) = 1 + i*x − x^2/2 + i*x^3/6 − x^4/24 + … =
(1−x^2/2−x^4/24+…)+i*(x+x^3/6+…) = cos(x)+i*sin(x)
exp(y+i*x) = exp(y)*exp(i*x) = exp(y)*(cos(x)+i*sin(x))
exp(y−i*x) = exp(y)*(cos(x)−i*sin(x))
da cui, sommando: exp(y+i*x)+exp(y−i*x) = 2*exp(y)*cos(x)
Le armoniche hanno la caratteristica di assumere valori massimo e minimo solo sul contorno del loro dominio; inoltre se si annullano sul contorno del dominio allora si annullano in tutto il dominio.
• La seguente equazione è detta EQUAZIONE DELLE ONDE (in una dimensione).
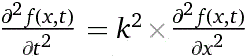
Con:
d^2/dt^2( f(x,t) ) = k^2*(d^2/dx^2( f(x,t) ) )Ottengo:
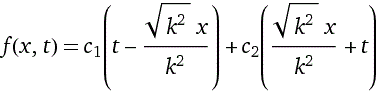
f(x,t) = c1(t-x/k) + c2(x/k+t)dove, anche in questo caso, c1 e c2 sono simboli funzionali.
È facile verificare direttamente che questa (al variare di c1 e c2)
è una soluzione.
Se la variabile t indica il tempo, c1(t-x/k) rappresenta una forma d'onda che si propaga lungo l'asse x;
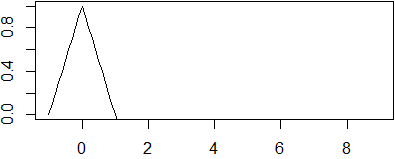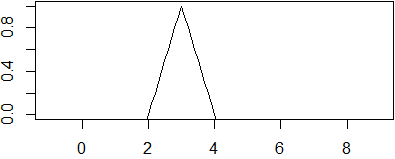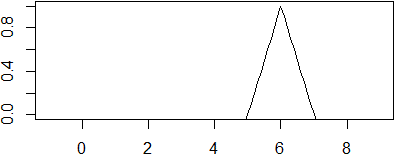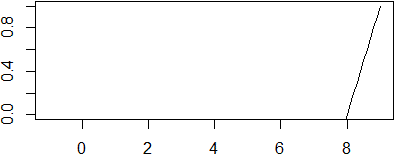
cosa analoga vale per c2(x/k+t). Un esempio: −|t-x|+1 (eseguendo in R la riga
seguente, cliccando via via sull'immagine che viene prodotta, ottieni quanto segue subito dopo):
f <- function(x) -abs(t-x)+1; for(t in 0:9) {plot(f,-1,9,ylim=c(0,1)); locator(1)}
•
Idea: un piccolo oggetto posto in un'ambiente a temperatura costante T ha temperatura f(t) che varia
con velocità proporzionale alla differenza di temperatura dall'ambiente:
Più complessa è la seguente EQUAZIONE DEL CALORE (in 1 dimensione).
Se f(x,t) è la temperatura all'istante t e nella posizione x di un'asta isolata, l'equazione seguente
rappresenta la diffusione del calore nell'asta stessa.
Limitiamoci a verificare che la funzione in x e t a destra ne è soluzione:
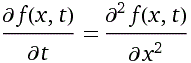
![]()
d/dt ( f(x,t) ) = d^2/dx^2 ( f(x,t) ) f(x,t) = t^(-1/2)*exp(-x^2/(4*t)) d/dt ( t^(-1/2)*exp(-x^2/(4*t)) ) = d^2/dx^2 ( t^(-1/2)*exp(-x^2/(4*t)) )Verifichiamo, analogamente, la cosa nel caso piano, ossia che la funzione in x, y e t a destra è soluzione dell'equazione alle derivate parziali seguente:
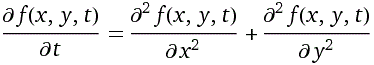
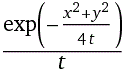
f(x,y,t) = exp(-(x^2+y^2)/(4*t))/t d/dt(exp(-(x^2+y^2)/(4*t))/t) = (d^2/dx^2(exp(-(x^2+y^2)/(4*t))/t))+(d^2/dy^2(exp(-(x^2+y^2)/(4*t))/t))