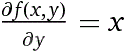
EQUAZIONI ALLE DERIVATE PARZIALI

Le equazioni differenziali alle derivate parziali (ossia che coinvolgono le derivate parziali della funzione incognita rispetto a piu' di una variabile), a differenza di quelle ordinarie, hanno soluzioni che non dipendono da costanti arbitrarie ma da funzioni arbitrarie.

•  Vediamo un primo es. di eq. a derivate parziali (l'incognita è f):

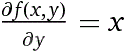
Siamo in grado di risoverla direttamente: la derivata rispetto a y di z è x se z è del tipo x*y; ma si può addizionare un qualunque termine che non contenga y, in quanto la sua derivata rispetto a y è zero. Quindi le soluzioni sono del tipo:  x*y+g(x) con g(x) funzione arbitraria.
Verifichiamo la cosa con WolframAlpha: 

d/dy f(x,y) = x
f(x,y) = c1(x) + x*y
•  OK.  Altro esempio.

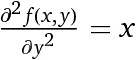
x*y^2/2 è evidentemente una soluzione. Ma lo rimane se si aggiunge qualcosa che derivato due volte rispetto a y dà 0:  x*y^2/2 + g(x) + h(x)*y.  Verifichiamolo con WolframAlpha: 

d^2/dy^2 f(x,y) = x
f(x,y) = y*c2(x)+c1(x)+(x*y^2)/2
•  OK.  Risolvi ("ragionando", e poi con WolframAlpha):

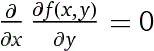
d/dx d/dy f(x,y) = 0
f(x,y) = c1(x)+c2(y)

•  Ci soffermeremo su solo alcune eq. differenziali a derivate parziali del secondo ordine che si impiegano spesso per modellizzare fenomeni di tipo fisico e tecnologico.

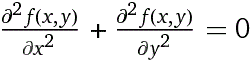
È la cosiddetta EQUAZIONE DI LAPLACE (o DEL POTENZIALE) in 2 dimensioni. Una funzione (continua con le sue derivate prime e seconde) che la soddisfa viene chiamata "armonica" (la cosa è legata a collegamenti con le serie di Fourier che non esploriamo). Proviamo a trovarne qualcuna: un'idea può essere quella di far entrare la funzione esponenziale (che ha sé stessa come derivata) e le funzioni seno e coseno (che hanno il proprio opposto come derivata seconda). In particolare proviamo con  (x,y) → exp(kx)*cos(ky); è facile verificare direttamente che:

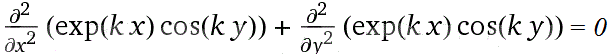
Verifichiamo per questa ed altre funzioni, per far prima, con WolframAlpha: 

d^2/dx^2 exp(k*x)*cos(k*y) + d^2/dy^2 exp(k*x)*cos(k*y) = 0

d^2/dx^2 exp(k*x)*sin(k*y) + d^2/dy^2 exp(k*x)*sin(k*y) = 0

d^2/dx^2 (3*x^2*y-y^3) + d^2/dy^2 (3*x^2*y-y^3) = 0

d^2/dx^2 (h*(x^2-y^2)+k*x*y) + d^2/dy^2 (h*(x^2-y^2)+k*x*y) = 0

d^2/dx^2 (x/(x^2+y^2)) + d^2/dy^2 (x/(x^2+y^2)) = 0  [per (x,y) ≠ (0,0)]

d^2/dx^2 log(x^2+y^2) + d^2/dy^2 log(x^2+y^2) = 0    [per (x,y) ≠ (0,0)]

Queste sono tutte soluzioni. Proviamo a risolvere in generale l'equazione di partenza, con WolframAlpha, e vediamo che cosa otteniamo: 

d^2/dx^2 f(x,y) + d^2/dy^2 f(x,y) = 0
f(x,y) = c1(y+i*x) + c2(y-i*x)
Otteniamo il termine  c1(y+i*x)+c2(y-i*x)  in cui compare l'unità immaginaria i e in cui, in questo caso, c1 e c2 indicano delle generiche funzioni. Quando, semplificando, in tale termine sparisce i, abbiamo una soluzione. Proviamo a vedere la forma di alcune soluzioni, e verifichiamo se esse sono effettivamente tali. Procediamo così:
– poniamo h = y+i*x, k = y-i*x;
– mettiamo l'espressione di c1(h)+c2(k) e semplifichiamola;
– calcoliamo d^2/dx^2 (…) + d^2/dy^2 (…) con tale espressione in … 

  Metto in WolframAlpha:
h=y+i*x, k=y-i*x, h^2+k^2
  Ottengo:
2*y^2-2*x^2
  Calcolo:
d^2/dx^2 (2*y^2-2*x^2) + d^2/dy^2 (2*y^2-2*x^2) = 0
  Ottengo:
True
  OK

h=y+i*x, k=y-i*x, h^2+i*h+k^2-i*k
-2*(x^2+x-y^2)
d^2/dx^2 (-2*(x^2+x-y^2)) + d^2/dy^2 (-2*(x^2+x-y^2)) = 0

h=y+i*x, k=y-i*x, exp(h)+exp(k)
2*exp(y)*cos(x)
d^2/dx^2 (2*exp(y)*cos(x)) + d^2/dy^2 (2*exp(y)*cos(x)) = 0

La semplificazione è stata ottenuta usando la formula di Eulero che lega l'esponenziale e le funzioni circolari nel campo complesso:
exp(x) = 1 + x + x^2/2 + x^3/6 + x^4/24 + … Sostituendo i*x a x:
exp(i*x) = 1 + i*x − x^2/2 + i*x^3/6 − x^4/24 + … = (1−x^2/2−x^4/24+…)+i*(x+x^3/6+…) = cos(x)+i*sin(x)
exp(y+i*x) = exp(y)*exp(i*x) = exp(y)*(cos(x)+i*sin(x))
 exp(y−i*x) = exp(y)*(cos(x)−i*sin(x))
da cui, sommando: exp(y+i*x)+exp(y−i*x) = 2*exp(y)*cos(x)

Le armoniche hanno la caratteristica di assumere valori massimo e minimo solo sul contorno del loro dominio; inoltre se si annullano sul contorno del dominio allora si annullano in tutto il dominio.

•  La seguente equazione è detta EQUAZIONE DELLE ONDE (in una dimensione).

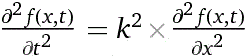
Con: 

d^2/dt^2( f(x,t) ) = k^2*(d^2/dx^2( f(x,t) ) )
Ottengo:

ovvero, per k > 0: 
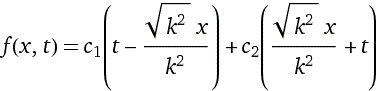
f(x,t) = c1(t-x/k) + c2(x/k+t)
dove, anche in questo caso, c1 e c2 sono simboli funzionali.

È facile verificare direttamente che questa (al variare di c1 e c2) è una soluzione.
Se la variabile t indica il tempo, c1(t-x/k) rappresenta una forma d'onda che si propaga lungo l'asse x; cosa analoga vale per c2(x/k+t). Un esempio: −|t-x|+1 (eseguendo in R la riga seguente, cliccando via via sull'immagine che viene prodotta, ottieni quanto segue subito dopo): 

f <- function(x) -abs(t-x)+1; for(t in 0:9) {plot(f,-1,9,ylim=c(0,1)); locator(1)}

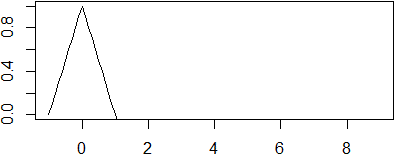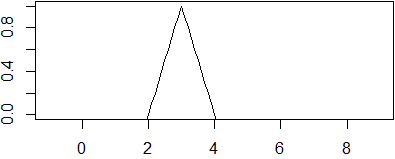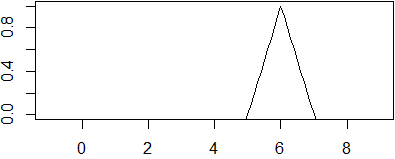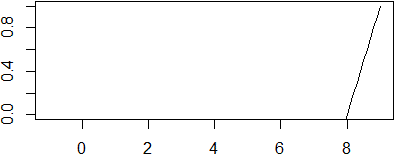
•  Idea: un piccolo oggetto posto in un'ambiente a temperatura costante T ha temperatura f(t) che varia con velocità proporzionale alla differenza di temperatura dall'ambiente:  d f(t) / dt = k(T-f(t)).  La soluzione è una esponenziale negativa:  f(t) = c1*exp(-k*t)+T
Più complessa è la seguente EQUAZIONE DEL CALORE (in 1 dimensione).  Se f(x,t) è la temperatura all'istante t e nella posizione x di un'asta isolata, l'equazione seguente rappresenta la diffusione del calore nell'asta stessa. Limitiamoci a verificare che la funzione in x e t a destra ne è soluzione:
        

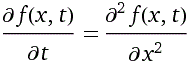
d/dt ( f(x,t) ) = d^2/dx^2 ( f(x,t) )
f(x,t) = t^(-1/2)*exp(-x^2/(4*t))
d/dt ( t^(-1/2)*exp(-x^2/(4*t)) ) =  d^2/dx^2 ( t^(-1/2)*exp(-x^2/(4*t)) )
Verifichiamo, analogamente, la cosa nel caso piano, ossia che la funzione in x, y e t a destra è soluzione dell'equazione alle derivate parziali seguente:
      
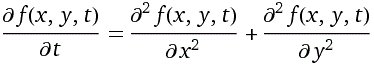
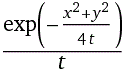
f(x,y,t) = exp(-(x^2+y^2)/(4*t))/t
d/dt(exp(-(x^2+y^2)/(4*t))/t) = (d^2/dx^2(exp(-(x^2+y^2)/(4*t))/t))+(d^2/dy^2(exp(-(x^2+y^2)/(4*t))/t))