(1)   (a) Calcolare il seguente integrale indefinito:
   ∫ (3x2 + 1) arctan(x − 1) dx
(b)  Utilizzando quanto trovato in (a), calcolare il seguente integrale definito:
  ∫1(3x2 + 1) arctan(|x| − 1) dx
−1

(a)  D(f·g) = D(f)·g + f·D(g)     D(f)·g = D(f·g) − f·D(g)
∫ (3x2 + 1) arctan(x − 1) dx = ∫ Dx(x3 + x) arctan(x − 1) dx =
(x3 + x) arctan(x − 1) − ∫ (x3 + x) 1/(1 + (x−1)2) dx = (x3+x) arctan(x−1) − ∫ (x3+x)/(x2−2x+2) dx =
(x3+x) arctan(x−1) − ∫ x+2 dx − ∫ (3x−4)/(x2−2x+2) dx =
(x3+x) arctan(x−1) − x2/2 − 2x − *
* = 3/2·∫ (2x −2)/(x2−2x+2) dx − ∫ 1/(x2−2x+2) dx = 3/2·log(x2−2x+2) − **
** = ∫ 1/((x−1)2+1) dx = arctan(x−1) + c
∫ (3x2 + 1) arctan(x − 1) dx = (x3+x) arctan(x−1) − x2/2 − 2x − 3/2·log(x2−2x+2) + arctan(x−1) + c =
(x3+x+1) arctan(x−1) − x2/2 − 2x − 3/2·log(x2−2x+2) + c
Con Maple potrei controllare tutti i passaggi, e il risultato finale:
> Int((3*x^2+1)*arctan(x-1), x) = int((3*x^2+1)*arctan(x-1), x);  simplify(");
ottenendo, a meno di equivalenze algenriche, gli stessi risultati.
Potrei controllare graficamente il risultato anche usando Poligon.
[Nota: usando  quo(x^3+x, x^2-2*x+2, x); rem(x^3+x, x^2-2*x+2, x);  posso ottenere quoziente e resto della divisione tra i due polinomi]
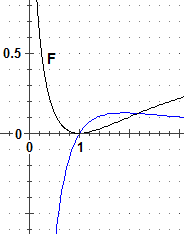
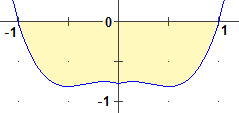
(b)  (3x2 + 1) arctan(x − 1) ha valori simmetrici rispetto ad x=0 in quanto x2 e |x| li hanno. Quindi:
  ∫1(3x2 + 1) arctan(|x| − 1) dx = 2 ∫1(3x2 + 1) arctan(x − 1) dx =
−10
2[0 − 1/2 − 2 − 0 − arctan(−1) + 0 + 0 + 3/2·log(2)] = π/2 + 3 log(2) − 5
Della simmetria potevamo accorgerci anche con un grafico. Ecco, qui sotto, quello realizzato con Poligon e la verifica dei calcoli con tale programma:
  F(x) = (3*x^2+1)*ATN(ABS(x)-1)
[-1,1] F INT = -1.349762131
PI/2-5+3*LOG(2) = -1.349762131525268
Il grafico e i calcoli li avrei, naturalmente, ottenuti anche con Maple, direttamente o sfruttando la simmetria rispeto all'asse y:
> int((3*x^2+1)*arctan(abs(x)-1),x=-1..1);  int(2*(3*x^2+1)*arctan(x-1),x=0..1);

(2)   (a) Calcolare (utilizzando un opportuno cambiamento di variabile) il seguente integrale indefinito:
   ∫ (et − e) / ( (1 − e−t) (et − e2) ) dt
(b)  Utilizzando quanto trovato in (a), determinare l'espressione esplicita della funzione integrale:
 F(x) = ∫xet − e dt
————————
1/2 (1 − e−t) (et − e2)
(c)  Della funzione F(x)
• determinare il campo di esistenza e limiti agli estremi;
• studiare continuità e derivabilità;
• stabilire crescenza e decrescenza;
• determinare il segno;
• tracciare un grafico qualitativo.

(a)  Il grafico della funzione integranda lo posso ottenere con Maple:
> g := t -> (exp(t)-exp(1))/((1-exp(-t))*(exp(t)-exp(2))); plot( f ,-5..5,-5..5)
o con Poligon: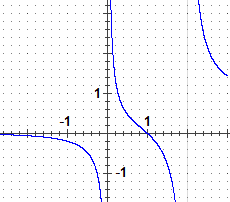

Facendo i calcoli a mano o con Maple:
> int(g(t),t); simplify(int(g(t),t));
si ottiene:   ( e log(et − e2) + log(et − 1) ) / (e + 1)   (+c)
Col cambiamento  u = exp(t)  avremmo potuto procedere con:
∫ (u − e) / ( (u − 1)(u − e2) ) du = … = ( log(u − e2) e + log(u − 1) ) / (e + 1) + c
da cui, sostituendo  u = exp(t)  avremmo avuto un'espressione equivalente a quella precedente.
(b)  F(x) = ( e log(ex − e2) + log(ex − 1) − e log(e1/2 − e2) − log(e1/2 − 1) ) / (e + 1)
(c)  Proviamo, prima, sperimentalmente:
g(x) = (EXP(x)-EXP(1))/((1-EXP(-x))*(EXP(x)-EXP(2)))
[1,0.1] g INT = -0.5344075976
[0.1,0.01] g INT = -0.6204905034
[0.01,0.001] g INT = -0.6194354619
[0.001,0.0001] g INT = -0.6192784957
A 0 non converge.
[1,1.9] g INT = -1.062422124
[1.9,1.99] g INT = -1.622483228
[1.99,1.999] g INT = -1.677236097
Neanche a 2 converge.
Il grafico di F (tracciato qui assieme a quello di g) sembra confermare la cosa:

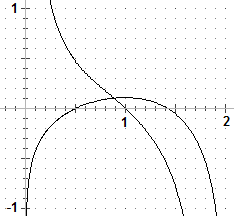
L'idea è che F sia definita e derivabile in (0,2) e che i limiti agli estremi siano -∞, che in 1 ci sia un punto di massimo e che a sinistra/destra di 1 F sia crescente/decrescente.
È facile verificare che D(F)(1) = 0.
F è continua. Per studiarne il segno studiamo dove F si azzera:
> fsolve(F(x) = 0, x, 0.1..1); fsolve(F(x) = 0, x, 1..1.9);
 .5000000000     1.434252808
Che F si azzerasse in 1/2 discendeva immediatamente dalla definizione (l'integrale in un punto, tra 1/2 e 1/2, è 0).

(3)   Si consideri la seguente funzione integrale:
 F(x) = ∫xlog(t) dt
————
1 t2 + √t
Senza calcolare l' integrale
• determinare il campo di esistenza della funzione F(x);
• stabilire se i limiti di F(x) agli estremi sono finiti o infiniti, utilizzando il criterio di convergenza per gli integrali impropri;
• studiare continuità e derivabilità di F(x);
• stabilire crescenza e decrescenza di F(x);
• determinare il segno di F(x);
• tracciare un grafico qualitativo di F(x).
Grafici, della funzione integranda e della funzione integrale, F, tracciati con Poligon (per il secondo, ad es., si è tracciato il grafico dell'integranda tra 0 e 40 e poi si è messo nel box y  =integr;  poi si è cliccato due volte [P] per memorizzare unite le due immagini).
 
Dai grafici (vedi sopra) o da prove numeriche:
G(x) = LOG(x)/(x^2+SQR(x))
[1,10] G INT = 0.5548412239   [1,80] G INT = 0.8145016792   [1,640] G INT = 0.8701994647
[1,10] G INT = 0.5548412239   [10,100] G INT = 0.2708707065   [100,1000] G INT = 0.04812403046   [1000,10000] G INT = 0.006886629191
ci si può convincere facilmente che F(x) → ∞ per x → 0+ e che F(x) → L < ∞ per x → ∞.
La verifica "teorica" (sulla base del criterio del confronto) è immediata:
l'integranda G(x) per x → 0+ è un infinito di ordine maggiore di 1 rispetto a 1/x (ha ordine maggiore di 2),
per x → ∞ è un infinitesimo di ordine maggiore di 1 rispetto a 1/x (ha ordine maggiore di 2).
La derivabiltà (e, quindi, continuità) di F è una conseguenza immediata della sua stessa definizione (ha per derivata la funzione integranda), così come (sulla base del segno della sua derivata) lo è il fatto che è crescente/decrescente per valori maggiori o uguali/minori o uguali ad 1. Segue, in particolare, che F ha valore minimo nel punto, 1, in cui ha derivata nulla, dove vale 0.