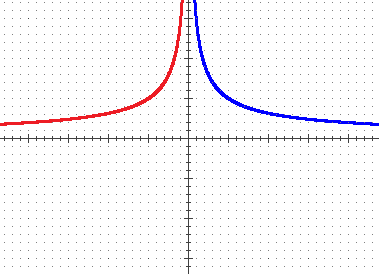
4, 5)  La prima funzione opera così: x → x² = u → 1 / ³√u = 1 / ³√(x²). La prima "freccia", l'elevamento al quadrato, dà lo stesso output a due input uno opposto dell'altro: 4 e -4 diventano entrambi 16. L'applicazione della seconda freccia, la radice cubica, non può reintrodurre una differenziazione. Quindi la funzione complessiva associa a input opposti lo stesso output; il grafico a sinistra dell'asse y deve quindi essere ottenibile come ribaltamento della parte a destra dell'asse y: vedi figura sotto a sinistra.

La seconda funzione opera così: x → x³ = u → 1 / ⁵√u = 1 / ⁵√(x³). Entrambe le "frecce" a input opposti associano output opposti (la prima associa 2 e -2 a 8 e -8, la seconda associa 32 e -32 a 2 e -2. Quindi anche la funzione complessiva associa a input opposti output opposti; il grafico a sinistra dell'asse y deve quindi essere ottenibile come ribaltamento della parte a destra dell'asse y e successivo ribaltamento attorno all'asse x (ossia una rotazione di 180°): vedi figura sopra a destra.

6)  Ecco i grafici di x → x, x → x², x → -x, x → 1/x, x → x³, x → 1/(x+3), x → (x-5)³+1, in ordine.

2 è simmetrico rispetto all'asse y.
1, 3, 4 e 5 sono simmetrici rispetto a (0,0).
6 è simmetrico rispetto a (-3,0).
[x → 1/(x+3) ha grafico ottenibile traslando con Δx = -3 quello di x → 1/x]
7 è simmetrico rispetto a (5,1).
[x → (x-5)³+1 ha grafico ottenibile traslando con Δx = 5 e Δy = 1 quello di x → x³]

7)  Dai grafici ricaviamo che 1/x ha valore superiore a 4 in un intervallo del tipo (0,k), dove k è l'ascissa del punto in cui si intersecano i due grafici (vedi figura sottostante). Algebricamente, risolvendo l'equazione 1/x = 4, troviamo che k = 1/4.
Quindi la disequazione è vera quando 0 < x < 1/4, ovvero le soluzioni sono i numeri dell'intervallo (0, 1/4).