(1) F(x) =
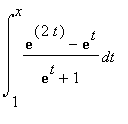 Calcolare
Calcolare 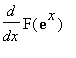
---------------------
(1) F(x) = 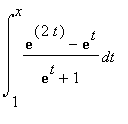 Calcolare
Calcolare 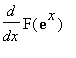
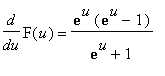
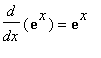
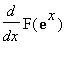 =
= 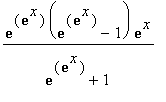
Controllo con Maple:
| > | D(F)(exp(x)); |
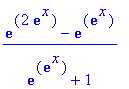
--------------------------
(2) Derivata prima di 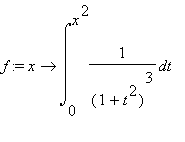
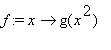 dove
dove 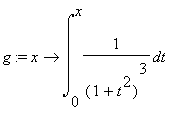
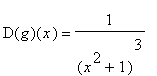
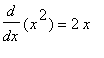
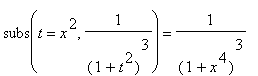
![]() =
= 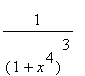
![]()
Controllo con Maple:
| > | simplify(diff(f(x),x)); |
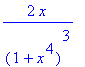
--------------------------
(3) Data 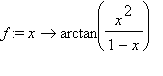 schizzare il grafico di
schizzare il grafico di 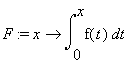
Vediamo cosa riusciamo a capire dai grafici, cercando di evitare troppi calcoli. Indico con g(x) l'argomento dell'arcontangente.
Eseguendo la divisione con resto tra i due termini di g(x) trovo: 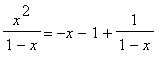
Dai grafici della retta y=-x-1 e della iperbole y=1/(1-x) posso dedurre l'andamento del grafico di y = g(x)![[Maple Plot]](../2005/90506s/90506s47.gif)
![[Maple Plot]](../2005/90506s/90506s48.gif)
Comunque: D(g)(x) = 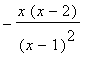 č positivo per x e (x-2) discordi, ossia 0 < x < 1 o 1 < x < 2, nullo per x = 0 o x =2, negativo altrove. Quindi g ha massimo realtivo in 2 (dove vale -4) e minimo relativo in 0 (dove vale 0) e asintoto verticale in 1.
č positivo per x e (x-2) discordi, ossia 0 < x < 1 o 1 < x < 2, nullo per x = 0 o x =2, negativo altrove. Quindi g ha massimo realtivo in 2 (dove vale -4) e minimo relativo in 0 (dove vale 0) e asintoto verticale in 1.
Posso anche controllare che il grafico di g ha effettivamente concavitā verso l'alto / il basso a sinistra / destra di x=1. Infatti g"(x) = 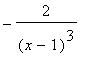 .č positivo / negativo per x inferiore /maggiore di 1.
.č positivo / negativo per x inferiore /maggiore di 1.
f(x) = arctan(g(x)) ha per dominio quello di g (essendo arctan definita su R). arctan cresce, quindi f(x) ha gli stessi intervalli di crescenza / descrescenza di g. f(x) č compreso strettamente tra ![]() e
e ![]() . Per x-> 1+ g(x) ->
. Per x-> 1+ g(x) -> ![]() e quindi f(x) ->
e quindi f(x) -> ![]() . Per x-> 1- g(x) ->
. Per x-> 1- g(x) -> ![]() e quindi f(x) ->
e quindi f(x) -> ![]() .
.
Al di lā della concavitā possiamo dedurre che f ha un grafico del tipo seguente:![[Maple Plot]](../2005/90506s/90506s57.gif)
F č definta e contuna ovunque in quanto l'integranda f č continua e limitata in R-{0}
D(F) = f, per cui F(x) cresce per x < 1, dove ![]() con f(x)=0 solo per x=0, e descresce per x > 1. Per x=1 si ha un massimo assoluto.
con f(x)=0 solo per x=0, e descresce per x > 1. Per x=1 si ha un massimo assoluto.
Qui y=F(x) ha un punto angoloso in quanto le derivate da destra e da sinistra hanno valori numerici diversi.
F" = D(f), per cui y = F(x) ha un punto di flesso a tangente orizzontale per x=0 dove f'(x) ha un minimo relativo e f'(x)=0.
In definitiva il grafico di F ha il seguente andamento (c'č un flesso anche per x=2, dove f'(x) ha un massimo relativo, anche se sul grafico tracciato col computer non si vede):![[Maple Plot]](../2005/90506s/90506s59.gif)
--------------------------
(4) 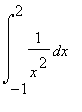
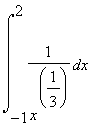 (in Maple:
(in Maple: 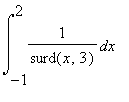
In Maple la radice n-esima si indica surd(x,n); x^(1/n) non sarebbe definito (almeno non nel modo usuale) per x negativo.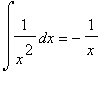 (+ c) ma
(+ c) ma 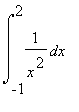 non č -1/2 - (-1/(-1)) = -3/2 in quanto in 0 l'integranda non č definita.
non č -1/2 - (-1/(-1)) = -3/2 in quanto in 0 l'integranda non č definita.
Occorre studiare l'integrale improprio. 1/x^2 per x->0 č infinto di ordine superiore a 1, per cui l'integrale non converge.
Con Maple:
| > | Int(x^(-2),x=-1..2) = int(x^(-2),x=-1..2); |
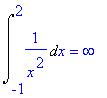
Invece 1/x^(1/3) per x->0 č un infinito di ordine minore di 1 per cui l'integrale converge.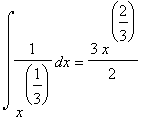 (+ c) Sia g(x) =
(+ c) Sia g(x) = 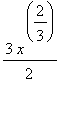
L'integrale tra 0 e 2 č il limite per x che tende a 0+ dell'integrale tra 0 e 2, ossia il limite di g(2)-g(x) che essendo g continua coincide con g(2)-g(0).
L'integrale tra -1 e 0 č il limite per x che tende a 0- dell'integrale tra -1 e x, ossia il limite di g(x)-g(-1) che essendo g continua coincide con g(0)-g(-1).
Dunque l'integrale tra -1 e 2 č g(2)-g(0) + g(0)-g(-1) = g(2)-g(-1)
In pratica abbiamo operato come si l'integranda fosse stata definita anche in 0.
Una cosa analoga accade tutte le volte che le primitive dell'integranda sono prolungabili per continuitā nel punto in cui l'integranda non
č definita.
In definita il nostro integrale vale 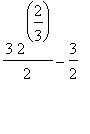
Contollo con Maple:
Ogni primitiva di 1/x^(1/3) sono definite e continue su tutto R per cui il loro limite per x->0 coincide col loro valore in 0. Dunque l'integrale tra 0 e A di 1/x^(1/3) coincide con
| > | 'int(1/surd(x,3),x=-1..2)' = int(1/surd(x,3),x=-1..2); 'int(1/surd(x,3),x=-1..2)' = evalf(int(1/surd(x,3),x=-1..2)); |
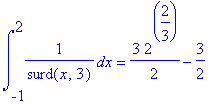
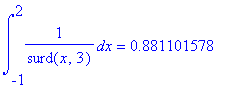
Se non avessi usato "surd" avrei ottenuto un valore strano:
| > | Int(x^(-1/3),x=-1..2) = int(x^(-1/3),x=-1..2); |
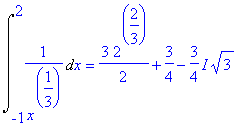
dovuto al fatto che Maple di fronte a x^(1/3) trova un numero che al cubo fa x ma che, se x<0, potrebbe essere un numero complesso invece che reale (prossimamante vedremo perché):
| > | (-1)^(1/3) = evalf((-1)^(1/3)); |
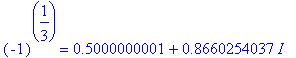
-------------------------
(5) Data 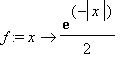 tracciare il grafico di
tracciare il grafico di 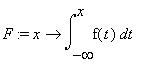
Il grafico di f è grafico simmetrico rispetto all'asse y;
per x negativo coincide con quello di y = exp(x)/2:![[Maple Plot]](../2005/90506s/90506s75.gif)
f č continua su R. Se esiste l'integrale improprio di f tra ![]() e h per un qualunque h, anche F ha come dominio R, altrimenti F ha dominio vuoto.
e h per un qualunque h, anche F ha come dominio R, altrimenti F ha dominio vuoto.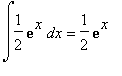 (+ c) Il limite per x ->
(+ c) Il limite per x -> ![]() di exp(x)/2 esiste ed č uguale a 0.
di exp(x)/2 esiste ed č uguale a 0.
Dunque, per x minore o uguale a 0: 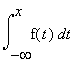 = exp(x)/2 - 0 = exp(x)/2.
= exp(x)/2 - 0 = exp(x)/2.
Essendo f pari (grafico simmetrico rispetto asse x) ho che F ha grafico simmetrico rispetto al suo punto di ascissa 0.
f (=F') č positiva per cui F cresce. F(1) = exp(0)/2 = 1/2. Per simmetria 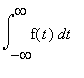 = 1, ossia F(x) -> 1 per x ->
= 1, ossia F(x) -> 1 per x -> ![]()
In 0 f (=F') ha un massimo, per cui il grafico di F cambia concavitā: ha un flesso ascendente con pendenza 1/2 (=f(0)).![[Maple Plot]](../2005/90506s/90506s82.gif)
Controllo con Maple:
| > | f:= x -> exp(-abs(x))/2; 'int(f(t),t=-infinity..x)' = int(f(t),t=-infinity..x); |
![]()
![int(f(t),t = -infinity .. x) = PIECEWISE([1/2*exp(x), x <= 0],[-1/2*exp(-x)+1, 0 < x])](../2005/90506s/90506s84.gif)