(1)
> restart;
> f := x -> cos(x);
> a := 0.5;
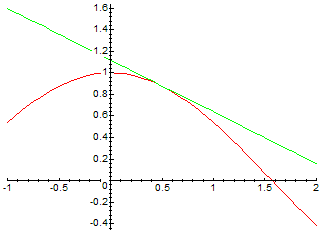
> g := x -> f(a)+D(f)(a)*(x-a);
> plot({f,g}, -1..2);
   
> taylor(F(x), x=c);
F(c) + D(F)(c)(x-c) + 1/2 (D⁽²⁾)(F)(c))(x-c)² + 1/6 (D⁽³⁾)(F)(c))(x-c)² + 1/24 (D⁽⁴⁾) (F)(c))(x-c)⁴ + (1/120 (D⁽⁵⁾)(F)(c))(x-c)⁵+O((x-c)⁶)
> taylor(f(x), x=0); taylor(f(x), x=0, 2); taylor(f(x), x=0, 8);
1 - 1/2 x² + 1/24 x² + O(x⁶)     1 + O(x²)     1 - 1/2 x² + 1/24 x² - 1/720 x⁶ + O(x⁸)
o(f(x)) = g(x) per x->h : f(x) e' trascurabile rispetto a g(x) per x->h
O(f(x)) = g(x) per x->h : f(x) e' trascurabile o dello stesso ordine rispetto a g(x) per x->h
> taylor((1+x)^N, x=0);
1 + N x + (1/2 N (N-1)) x² + (1/6 N (N-1) (N-2)) x³ + (1/24 N (N-1) (N-2) (N-3)) x⁴ + (1/120 N (N-1) (N-2) (N-3) (N-4)) x⁵ + O(x⁶)
> taylor((1+x)^5, x=0); taylor((1+x)^5, x=0, 3);
1 + 5x + 10x² − 10x³ + 5x⁴ + x⁵     1 + 5x + 10x² + O(x³)
> taylor(sin(x), x=0, 4);
x − 1/6 x³ + O(x⁵)
> convert(taylor(sin(x), x=0, 4), polynom);
x − 1/6 x³
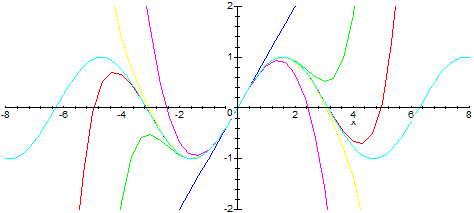
> a := 0; f:= x -> sin(x); plot( {f(x),convert(taylor(f(x), x=a, 3), polynom), convert(taylor(f(x), x=a, 5), polynom), convert(taylor(f(x), x=a, 7), polynom), convert(taylor(f(x), x=a,9 ), polynom), convert(taylor(f(x), x=a, 11), polynom)}, x=-8..8, -2..2);

------------------------
(2)   Il comando series generalizza il comando taylor (vedi gli help).
> taylor(log(1+x), x=0);
x − 1/2 x² + 1/3 x³ - 1/4 x⁴ + 1/5 x⁵ + O(x⁶)
> taylor(sqrt(sin(x)), x=0);
Error, does not have a taylor expansion, try series()
> taylor(log(1+x), x=0); series(log(1+x), x=0);
x − 1/2 x² + 1/3 x³ - 1/4 x⁴ + 1/5 x⁵ + O(x⁶)     x − 1/2 x² + 1/3 x³ - 1/4 x⁴ + 1/5 x⁵ + O(x⁶)
> series(sqrt(sin(x)), x=0);
x^1/2 − 1/12 x^5/2 + 1/1440 x^9/2 + O(x^11/2)
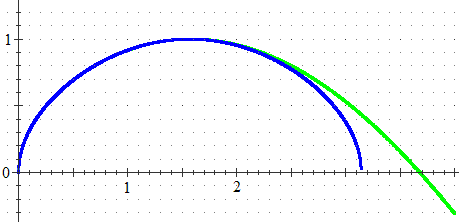
> plot ({x-> sqrt(sin(x)), x-> x^(1/2)-1/12*x^(5/2)+1/1440*x^(9/2)}, 0..4.5);

Nota 1.  Per Poligon e per altro software in 0  "…^(1/2)"  non è definito. Per avere la definizione anche in questo punto occorre usare opportunamente la radice quadrata (SQR o SQRT in Poligon):
h(x) = sqr(x)-1/12*sqr(x)^5+1/1440*sqr(x)^9
Nota 2.  Il comando series di Maple consente di studiare, in generale, le serie di funzioni (vedi), mentre taylor permette di studiare solo le serie di Taylor.
-----------------------------
(3)   Rivediamo, con Maple, l'approssimazione polinomiale a partire da 0 di x → sin(x²)-sin(x)²
> taylor(sin(x^2)-sin(x)^2, x=0);
1/3 x⁴ + O(x⁶)