Convergenza uniforme e non
(1)
Successione di funzioni che a N associa la funzione che trasforma x in x^N:
fn(x) = x^n se x sta in [0,1].
Rappresentiamo la successione con la funzione
F: (n,x) → fn(x)
> restart;
> F:= (n,x) -> x^n;
Vediamo ad es. i valori che le funzioni f1, f2, f3 assumono in 1/2
> F(1, 1/2); F(2, 1/2); F(3, 1/2);
1/2 1/4 1/8
> plot ([F(1,x), F(2,x), F(3,x), F(4,x), F(50,x)], x=0..1);
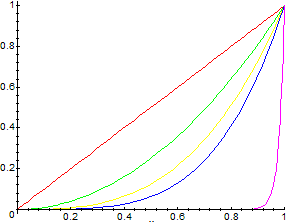
Per n → ∞ fn → G dove G(x) = 0 per x in [0,1), G(1) = 1.
Infatti, comunque fissi x in [0,1],
fn(x) → G(x), ossia dato ε posso trovare n tale che il punto di ascissa x del grafico di fj con
j ≥ n
dista meno di ε dal grafico di G, ossia il segmento dell'asse x tra 0 e 1 escluso al più il punto (1, 1).
Questa convergenza è solo "puntuale", non "uniforme":
fissato ε non riesco a trovare n tale che da lì in poi x^n (ovunque sia x in [0,1]) disti da G(x) meno di ε; il massimo scarto si mantiene uguale ad 1 (vedi l'esempio negli appunti).
(2) Date
1/(1+x)2 e 1/(1+x)3,
trovarne le serie di Taylor attorno a 0 a partire dallo sviluppo di (vedi)
1/(1-x) (convergenza tra -1 e 1)
utilizzando il fatto che la somma della serie delle derivate coincide con la derivata della somma della serie
(se vuoi vedi http://macosa.dima.unige.it/mat/calculus/seriesf.htm per richiami)
> taylor(1/(1-x), x=0);
1 + x + x^2 + x^3 + x^4 + x^5 + O(x^6)
> diff(1/(1-x),x);
1/(1−x)2
Derivando i tremini della serie precedente trovo lo sviluppo in serie di 1/(1−x)2
> taylor(1/(1-x)^2, x=0);
1 + 2 x + 3 x^2 + 4 x^3 + 5 x^4 + 6 x^5 + O(x^6)
da cui ricavo quello di 1/(1+x)^2 … (1 − 2 x + 3 x^2 − 4 x^3 + …)
Si procede analogamente per 1/(1+x)^3 (1 − 3 x + 6 x^2 − 10 x^3 + …)
(3) (a) Si calcoli il raggio di convergenza della serie
∑ n=1..∞ n(x−2)n / 2n
e (b) se ne calcoli la somma per x = 1.
(a) Criterio del rapporto
> a:= n -> n/2^n*(x-2)^n; abs(a(n+1)/a(n)); simplify(abs(a(n+1)/a(n)));
n
n (x - 2)
a := n -> ----------
n
2
| n + 1 n
|(n + 1) (x - 2) 2 |
|-----------------------|
| n + 1 n |
| 2 n (x - 2) |
|(n + 1) (x - 2)|
1/2 |---------------|
| n |
> R := limit (simplify(abs(a(n+1)/a(n))), n=infinity);
R := 1/2 | x - 2 |
Grafico di R in funzione di x:
> plot(R, x=-1..5);
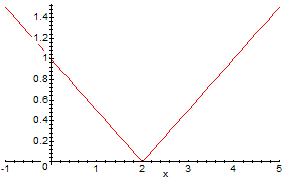
R minore di 1 per x in (0,4). Del resto, con Maple:
> solve(R < 1, x);
RealRange(Open(0), Open(4))
Negli estremi si ha divergenza in quanto a(n) in entrambi i casi non tende a 0:
Per x=4
> Sum(n/2^n*(4-2)^n, n=1..infinity) = sum(n/2^n*(4-2)^n, n=1..infinity);
∑ n=1..∞ n = ∞
controllo:
>
sum(n/2^n*(4-2)^n, n=1..10); sum(n/2^n*(4-2)^n, n=1..11); sum(n/2^n*(4-2)^n, n=1..k);
55 66 (k+1)2/2 − k/2 − 1/2
Per x=0
> Sum(n/2^n*(0-2)^n, n=1..infinity) = sum(n/2^n*(0-2)^n, n=1..infinity);
∑ n=1..∞ n(-2)n/2n = -1/4
oppure undefined
a seconda della versione di Maple;
controllo:
>
sum(n/2^n*(0-2)^n, n=1..9); sum(n/2^n*(0-2)^n, n=1..10); sum(n/2^n*(0-2)^n, n=1..11);
sum(n/2^n*(0-2)^n, n=1..12); expand(sum(n/2^n*(0-2)^n, n=1..k));
−5 5 −6 6
(-1)kk/2 + (-1)k/4 - 1/4
diverge.
(b) Per x = 1:
>
Sum(n/2^n*(1-2)^n, n=1..infinity) = sum(n/2^n*(1-2)^n, n=1..infinity);
∑ n=1..∞ n(-1)n/2n = −2/9
controllo:
> evalf(sum(n/2^n*(1-2)^n, n=1..30)); evalf(sum(n/2^n*(1-2)^n, n=1..31));
−.2222222127 −.2222222271
Questo valore è stato ottenuto con Maple. La cosa potrebbe essere ottenuta riordinando opportunamente la serie, come può
suggerire il seguente calcolo ottenuto con Maple (chi vuole, ci ragioni su):
>
Sum(n/2^n*(1-2)^n, n=1..2*k) = simplify(sum(n/2^n*(1-2)^n, n=1..2*k));
∑ n=1..2k n (-1)n / 2n =
2 / 3 · 4−k k + 2 / 9 · 4−k − 2 / 9
o ricorrendo alla somma della seguente serie (il cui studio, come si è visto, è
ricavabile differenziando la serie geometrica):
>
-1/(1+x)^2 = taylor(-1/(1+x)^2, x);
−1/(1+x)2 =
− 1 + 2x − 3x2 + 4x3 − 5x4 + 6x5 + O(x6)
>
Sum(n*x^(n-1)*(-1)^n, n=1..infinity) = sum(n*x^(n-1)*(-1)^n, n=1..infinity);
∑ n=1..∞ n (-1)n xn−1 = −1/(1+x)2
Dunque:
>
-x/(1+x)^2 = series(-x/(1+x)^2,x);
-x/(1+x)^2 = Sum(n*x^n*(-1)^n,n=1..infinity);
−x/(1+x)2 =
− x + 2x2 − 3x3 + 4x4 − 5x5 + O(x6)
−x/(1+x)2 =
∑ n=1..∞ n (-1)n xn
La nostra serie corrisponde al caso x = 1/2:
>
subs(x=1/2, -x/(1+x)^2 = Sum(n*x^n*(-1)^n,n=1..infinity));
sum(n*(1/2)^n*(-1)^n,n=1..infinity);
−2/9 =
∑ n=1..∞ n (-1)n (1/2)n
−2/9

