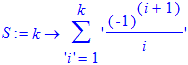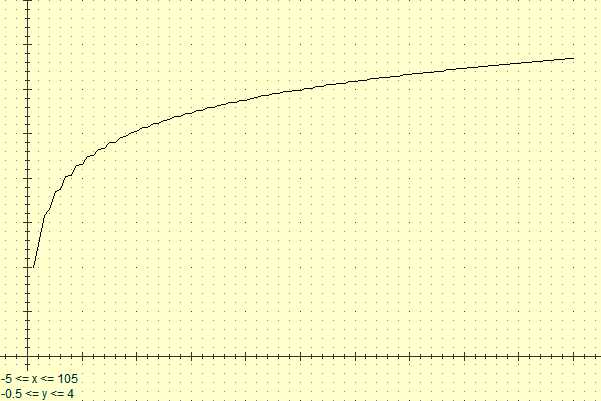(continuazione)
(3) Una somma che dipende da una variabile
g(x) = 1 + x/2 + x^2/3 + x^3/4 + ...
> sum('x^(n-1)/n', 'n'=1..10); g := x -> sum('x^(n-1)/n', 'n'=1..infinity);
1+x/2+x2/3+x3/4+x4/5+x5/6+x6/7+x7/8+x8/9+x9/10
g:= x → ∑ 'n' = 1..∞ 'x(n−1) / n'
Con qualche versione di Maple (le più vecchie) ottengo:
> g(1); g(-1); g(1/2); g(-2); g(x);
∞ ln(2) 2 ln(2) ln(3)/2 −ln(1−x)/x
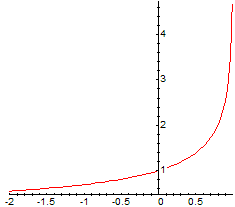
> plot(g, -2..0.99);
Con altre ho:
> g(1); g(-1); g(1/2); g(-2); g(x);
∞ ln(2) 2 ln(2) undefined −ln(1−x)/x
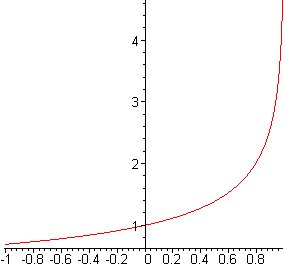
e ho il grafico non col comando precedente, ma con:
> plot(g, -1..0.99);
In qualche situazione le uscite di Maple possono ingannare.
La somma, quando esiste, è −ln(1−x)/x,
ma in qualche caso, ad es. per x = −2, pur essendo −ln(1−x)/x definito,
questo non è la somma della serie, che per tale valore di x non converge.
In ogni caso, con qualunque versione di Maple,
posso controllare numericamente che cosa succede:
> evalf(sum('(-1)^(n-1)/n', 'n'=1..100)); evalf(sum('(-1)^(n-1)/n', 'n'=1..101));
.6881721793 .6980731694
> evalf(sum('(-1.1)^(n-1)/n', 'n'=1..100)); evalf(sum('(-1.1)^(n-1)/n', 'n'=1..101));
-64.63485623 71.80685011
Alle stesse conclusioni potrei arrivare con qualche ragionamento non sperimentale.
Con Poligon:
F(x) = #x^(x-1)/x
#x=1/2
[1,10] F SUM
[1,1000] F SUM
[1,1001] F SUM
2*LOG(2)=
#x=-1
[1,10] F SUM
[1,4000] F SUM
[1,4001] F SUM
LOG(2)=
#X=-1.1
[1,100] F SUM
[1,101] F SUM
| |
= 1.386129712
= 1.386294361
= 1.386294361
1.386294361119891
= 0.6456349206
= 0.6930221962
= 0.6932721337
0.6931471805599453
= -64.63485623
= 71.80685011
|
Vediamo, ad es., come avremmo potuto procedere direttamente
per x = -1: 1 - 1/2 + 1/3 - 1/4 + 1/5 ...
> S:= k -> sum('1/i*(-1)^(i+1)', 'i'=1..k);
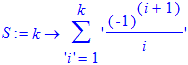
> S(1); S(2); S(3); S(4); S(5); evalf(S(100)); evalf(S(101)); S(infinity);
1 1/2 5/6 7/12 47/60
.6881721793 .6980731694 ln(2)
> f:= x -> S(round(x));
> plot(f,1/2..20+1/2, 0..1.2);
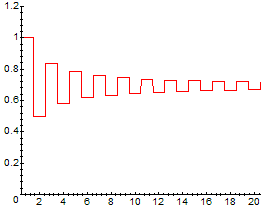
Con Poligon:
(copia e aziona CLP) |
F(x)=#X^(x-1)/x
#x=-1
noscrivi=1
N
scala sx:-5..205 sy:-0.1..1.1
FOR #N=1 TO 200 : #S=[1,#N] F SUM ; PLOT X:#N Y:#S
noscrivi=0
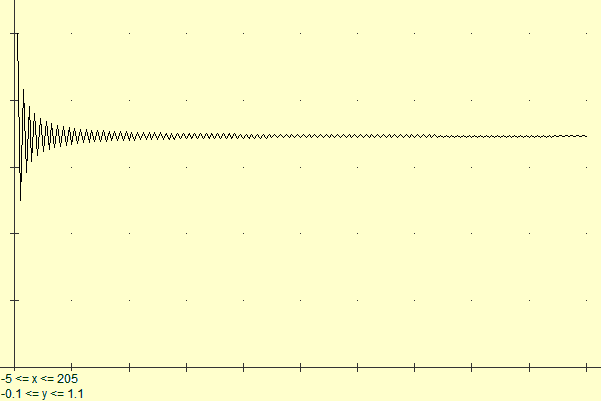 |
(noscrivi serve solo per evitare le scritte dei calcoli effettuati nel corso del ciclo)
Nota.
> limit(S(k), k = infinity);
undefined
> S(infinity);
ln(2)
Nonostante che S(infinity) sia il limite per k che tende a ∞ di S(k),
in Maple non si ha, se non in casi particolari, l'eguaglianza delle due termini: il modo in cui viene
calcolato il primo differisce dal modo in cui, in genere, da Maple vengono calcolati i limiti.
Occorre, quindi, usare S(infinity).
------------------
(4) Serie con espressione diversa per i pari e i dispari
1 - 1/4 + 1/3 - 1/16 + 1/5 - ...
a(n) = 1/n^2 per n pari
a(n) = 1/n per n dispari
somma (-1)^n * a(n) Come descriverla? Ad esempio (usando il comando trunc - vedi l'help o qui):
> a:= n -> (piecewise(trunc(n/2)*2=n, 1/n^2, trunc(n/2)*2<n, 1/n));
> a(1); a(2);
1 1/4
> S := k -> sum('a(i)*(-1)^(i+1)', 'i'=1..k);
> S(1); S(2); evalf(S(100)); evalf(S(1000)); evalf(S(1001));
1 3/4 2.531491665 3.678325129 3.679324130
> f:= x -> S(round(x)); plot(f, 1/2..20+1/2, 0..2.5);
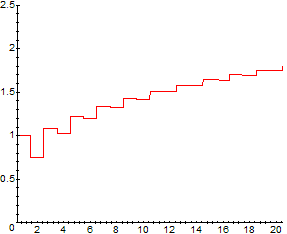
La serie diverge per le considerazioni viste in NOTA 4 degli appunti su
"Convergence Tests for Infinite Series"
Calcoli (e grafici) analoghi fatti con Poligon:
h(x)=(int(x/2)*2=x)*(1/x^2)+(int(x/2)*2<x)*(1/x)
N
scala sx:-5..105 sy:-0.5..4
noscrivi=1
FOR #N=1 TO 100 : #S=[1,#N] H SUM ; PLOT X:#N Y:#S
noscrivi=0
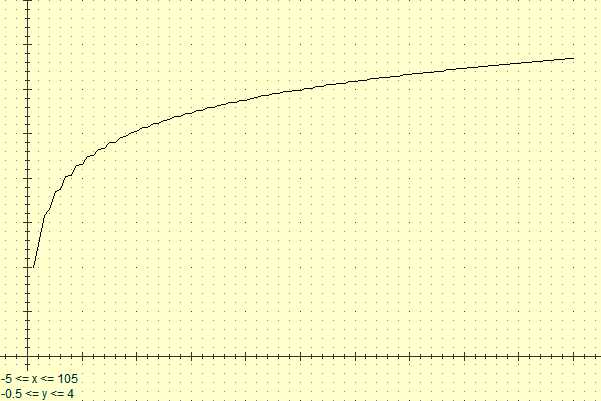
-----------------------------------------
(5) Esempi
> Sum((1+2^(n+1))/3^n, n=0..infinity)=sum((1+2^(n+1))/3^n, n=0..infinity);
∑ n = 0..∞ (1 + 2n+1) / 3n = 15/2
Come possiamo ottenere questo risultato a mano?
> Sum((1)/3^n, n=0..infinity)+Sum((2^(n+1))/3^n, n=0..infinity);
(∑ n = 0..∞ 1 / 3n) +
(∑ n = 0..∞ 2n+1 / 3n)
> Sum((1/3)^n,n=0..infinity)+Sum(2*(2/3)^n,n=0..infinity);
(∑ n = 0..∞ (1 / 3)n) +
(∑ n = 0..∞ 2(2/3)n)
> Sum((1/3)^n,n=0..infinity)+2*Sum((2/3)^n,n=0..infinity);
(∑ n = 0..∞ (1 / 3)n) +
2(∑ n = 0..∞ (2/3)n)
Ci siamo ricondotti a due serie geometriche. Possiamo usare la "formula" per la somma delle serie geometriche
> subs(x=1/3, 1/(1-x)) + 2*subs(x=2/3, 1/(1-x));
15/2
------------------------------
(6)
1/1 + 1/(1+2) + 1/(1+2+3) + 1/(1+2+3+4) + ...
Come descriverla con Maple?
> Sum(1/Sum(i, i=1..n), n=1..infinity);
(1+2+3+ ... +n) = (n+1)*n/2 = n^2 + o(n^2)
1 + 1/2^2 + ... + 1/n^2 + ... converge, quindi converge anche la nostra serie
La cosa puo' essere precisata col criterio del rapporto:
1/(1+2+3+ ... +n) / (1/n^2) = 1/( n^2 + o(n^2) ) / (1/n^2) --> 1
Vediamo come evolve la somma parziale;
> s:= k -> sum(1/sum(i, i=1..n), n=1..k);
> s(1); s(10); s(100); s(1000);
1 20/11 200/101 2000/1001
La somma parziale di ordine 100 è (202-2)/101 = 2-2/101. Quella di ordine n sembra essere 2(1-1/(n+1)).
Si vede che la somma parziale tende a 2. Controllo diretto:
> Sum(1/Sum(i, i=1..n), n=1..infinity) = sum(1/sum(i, i=1..n), n=1..infinity);
∑ n = 1..∞ 1 / (∑ i = 1..n i) = 2
Vediamo di arrivarci con un ragionamento invece che con Maple.
Idea: cerco di scomporre il termine n-esimo in una differenza (cerco di dare forma "telescopica" alla serie: vedi NOTA 5 degli appunti su
"Convergence Tests for Infinite Series").
> 1/((n+1)*n/2);
2 / (n(n+1))
> a/n-b/(n+1); simplify(a/n-b/(n+1)) = 1/((n+1)*n/2);
a / n − b / (n+1) (an+a−bn) / (n(n+1)) = 2 / (n(n+1))
Prendo a = b = 2. Controllo:
> 2/n-2/(n+1) = simplify(2/n-2/(n+1));
2 / n − 2 / (n+1) = 2 / (n(n+1))
Dunque la somma parziale di ordine n posso scriverla:
1/1 + 1/(1+2) + 1/(1+2+3) + 1/(1+2+3+4) + ... + 1/(1+2+3+ ... n) =
2 (1/2 + 1/(2*3) + 1/(3*4) + 1/(4*5) + ... + 1/(n*(n+1)) ) =
2 ((1/1-1/2) + (1/2-1/3) + (1/3-1/4) + (1/4-1/5) + ... + (1/n-1/(n+1)) ) =
2 (1 - 1/(n+1) ) −> 2
Abbiamo ritrovato quanto trovato sopra, OK
-----------------------
(7)
> Sum((1+sin(n))/n^2, n=1..infinity);
Posso usare il criterio del rapporto (con la somma degli 1/n^2)?
> Limit(((1+sin(n))/n^2)/(1/n^2), n=infinity) = limit(((1+sin(n))/n^2)/(1/n^2), n=infinity);
lim n → ∞ 1 + sin(n) = 0 .. 2
NO: il limite non esiste: la successione oscilla tra 0 e 2.
Posso pero' usare il criterio del confronto:
> 0 <= (1+sin(n))/n^2; (1+sin(n))/n^2 <= 2/n^2;
0 ≤ (1 + sin(n)) / n2
(1 + sin(n)) / n2 ≤ 2 / n2
1 + 1/4 + ... + 1/n^2 + ... converge e quindi converge anche la nostra serie
Grafico e calcoli, per conferma:
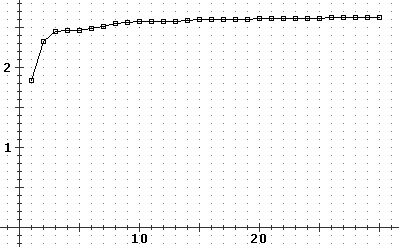 |
h(x)=(1+sin(x))/x^2
N
scala sx:-5..35 sy:-0.5..3
noscrivi=1
FOR #N=1 TO 30: #S=[1,#N] H SUM; PLOT X:#N Y:#S
noscrivi=0
:
: |
> evalf(sum((1+sin(n))/n^2, n=1..4000),20); evalf(sum((1+sin(n))/n^2, n=1..4001),20);
2.6586432508750793694 2.6586432519040733830
--------------------------
(8)
> Sum((2*n)!/(n!)^2, n=1..infinity);
> a:= n -> (2*n)!/(n!)^2;
Se compare un fattoriale ci si puo' aspettare che convenga usare il criterio del rapporto
> a(n+1)/a(n); simplify(a(n+1)/a(n));
... 2(2n+1) / (n+1)
> Limit(a(n+1)/a(n), n=infinity) = limit(a(n+1)/a(n), n=infinity);
lim n → ∞ ... = 4
4 > 1 quindi la serie diverge. Ce ne saremmo subito accorti con qualche conto:
> a(1); a(2); a(3); a(4);
2 6 20 70
-------------------
(9)
> Sum(n^5/2^n, n=1..infinity);
Criterio rapporto:
> a:= n -> n^5/2^n;
> a(n+1)/a(n); simplify(a(n+1)/a(n)); limit(a(n+1)/a(n), n=infinity);
... (n+1)5/(2n5) 1/2
----------------
(10)
> Sum(1/(1+sqrt(n)), n=1 ..infinity)=sum(1/(1+sqrt(n)), n=1 ..infinity);
∑ n = 1..∞ 1 / (1+√n) =
∑ n = 1..∞ 1 / (1+√n)
> s := k -> sum(1/(1+sqrt(n)), n=1 ..k); evalf(s(10)); evalf(s(100));
s := k -> ∑ n = 1..k 1 / (1+√n)
3.238236075 14.89606885
Sembra divergere. Col criterio del rapporto:
> b := n-> 1/(1+sqrt(n)):
> Limit( b(n+1)/b(n) ,n=infinity) = limit( b(n+1)/b(n) ,n=infinity);
lim n → ∞ (1+√n) / (1+√(n+1)) = 1
non posso concludere.
Ma posso stabilire la divergenza usando il criterio del confronto:
> 1+sqrt(n) < sqrt(n)+sqrt(n); 1/(1+sqrt(n)) > 1/(sqrt(n)+sqrt(n));
1+√n < 2√n
1/(2√n) < 1 / (1+√n)
-------------------------
(11)
> Sum((n+5)/(n^3-2*n+3), n=1..infinity) = sum((n+5)/(n^3-2*n+3), n=1..infinity);
∑ n = 1..∞ (n+5) / (n3−2n+3) =
∑ n = 1..∞ (n+5) / (n3−2n+3)
> Sum((n+5)/(n^3-2*n+3), n=1..infinity) = evalf(sum((n+5)/(n^3-2*n+3), n=1..infinity));
∑ n = 1..∞ (n+5) / (n3−2n+3) = 4.839316162
Converge in quanto a(n) = 1/n^2 + o(1/n^2)
-------------------
(12)
> Sum(1/i, i=1..infinity) = sum(1/i, i=1..infinity);
∑ i = 1..∞ 1 / i = ∞
Diverge, infatti:
1 + 1/2 + 1/3 + 1/4 + ... + 1/10 + 1/11 + ... + 1/100 + ... + 1/1000 + 1/1001 + ...
1 + (1/2+ 1/3 + 1/4 + ... + 1/10) + (1/11 + ... + 1/100 ) + (1/101+... +1/1000) + ...
1 + 0.9 + 0.9 + 0.9 + ...
-------------------------------
(13)
> Sum((n*cos(n*Pi))/2^n, n=1..infinity) = sum((n*cos(n*Pi))/2^n, n=1..infinity);
∑ n = 1..∞ (n cos(nπ)) / 2n = −2/9
Serie a segni alterni, in quanto:
> assume(k,integer):
> simplify(subs(n=2*k, cos(n*Pi))); simplify(subs(n=2*k+1, cos(n*Pi)));
1 −1
Annullo assunzione fatta su k:
> k := 'k':
Converge in quanto il termine ennesimo, uguale a (-1)^n * n/2^n, ha valore assoluto n/2^n che tende a 0 decrescendo.
Vediamo grafici di termine ennesimo e di somma parziale:
> a:= n-> (n*cos(n*Pi))/2^n: s:= k -> sum(a(n), n=1..k);
> f:= x -> a(round(x)): g:= x -> s(round(x)):
> plot (f, 0.5..20.5); plot (g, 0.5..20.5); evalf(s(100));
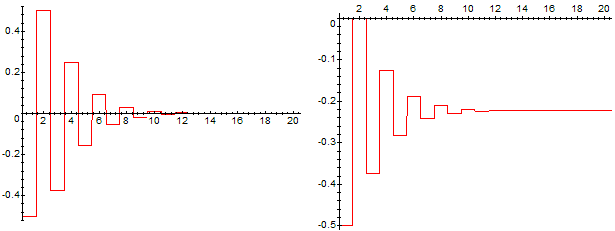
-.2222222222
(OK: -2/9 = -0.222…)
-------------------------------
Altri esercizi
(a) Studiare la convergenza di ∑ n = 1..∞ (-1)n+1 n / (10 n + 5)
(b) Studiare la convergenza di ∑ n = 1..∞ cos(π n) / n2
(c) Studiare la convergenza di ∑ n = 3..∞ (-1)n / log(log(n))
(d) Arrotondare ("a mano") a meno di 1/100 ∑ n = 0..∞ (-1)n / n!
-------------------------------
Nota
Function: trunc - truncate a number to the next nearest integer towards 0
> trunc(7); 7
> trunc(8/3); 2
> trunc(-2.4); -2