Soluzione esercizi
•  Studia la serie  Σ_{n = 1…∞} 1 / (n(n+1)) sperimentalmente, congettura il valore della somma, e prova a dimostrare che converge a questo valore (idea: in base alle uscite congettura l'espressione del valore della somma di ordine n in funzione di n, dimostra che la somma ha effettivamente questa espressione, e poi studiane il limite per n →∞).
È facile trovare (con Poligon o con Maple):
F(x) = 1/(x*(x+1))
[1,10] F SUM = 0.9090909090909091 = 10/11
[1,99] F SUM = 0.9899999999999997 = 99/100
[1,100] F SUM = 0.9900990099009898 = 100/101
e congetturare che la somma parziale (da 1 ad n) è n/(n+1) e che quindi la somma è 1. Rinviamo alla NOTA 5 del seguente documento la dimostrazione di questa congettura.
•  Studia la convergenza delle seguenti serie, prendendo, caso per caso, come h il numero naturale più piccolo per cui tutti i termini della serie sono definiti:
 Σ_{n = h…∞} (1 / log(n))
h = 2; con Maple il calcolo non viene svolto; posso provare a valutare la somma al crescere del secondo estremo di integrazione e con  evalf(sum(1/ln(n), n=2..100)); evalf(sum(1/ln(n), n=2..1000)); evalf(sum(1/ln(n), n=2..10000));  ottengo rispettivamente 29.99143755, 177.4388009, 1245.948262 convincendomi delle divergenza, che in questo caso è molto facile dedurre teoricamente:  1/log(n) > 1/n per n ≥ 2 e la divergenza viene dedotta da quella di ∑_n 1/n.
 Σ_{n = h…∞} (1 / (1+√n))
Vedi il punto 10 di questo documento
 Σ_{n = h…∞} ((2n)! / (n!)²)
Vedi il punto 8 di questo documento
 Σ_{n = h…∞} (2ⁿ⁺¹ / nⁿ)
h = 1; da Maple il calcolo non viene svolto simbolicamente, ma numericamente sì:  evalf(sum(2^(n+1)/n^n, n=1..infinity));  fornisce 6.741160310; la convergenza è molto rapida, infatti  evalf(sum(2^(n+1)/n^n, n=1..10));  e  evalf(sum(2^(n+1)/n^n, n=1..11));  danno 6.741160294 e 6.741160309. La convergenza in questo caso è facile da dedurre teoricamente:  la serie equivale a 2·Σ_{n = 1..∞} (2/n)ⁿ; per n > 2  (2/n)ⁿ ≤ (2/3)ⁿ, e Σ_{n = 1..∞} (2/3)ⁿ è una serie geometrica convergente.
 Σ_{n = h…∞} (cos(nπ) / log(n))
h = 2; da Maple il calcolo non viene svolto simbolicamente, ma numericamente sì:  evalf(sum(cos(n*Pi)/log(n), n=2..infinity));  fornisce .9242998972; la serie ha somma che converge oscillando: le somme per n da 2 a 2, da 2 a 3 e da 2 a 4 valgono rispettivamente 1.442695041, .5324558146, 1.253803335. La convergenza è abbastanza lenta: da 2 a 1000 e da 2 a 1001 abbiamo le somme .9966770049 e .8519330709. Scritta in maniera più "trasparente" la serie diventa  Σ_{n = 2…∞} (-1)ⁿ/log(n);  la convergenza deriva dal fatto che si tratta di una serie a segni alterni con l'elemento via via sommato che tende a 0.

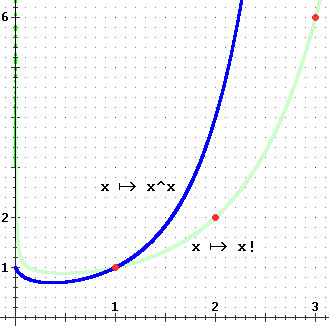
Σn = h…∞ (n! / nn) h = 1; da Maple il calcolo non viene svolto simbolicamente, ma numericamente sì:  evalf(sum(n!/n^n, n=1..infinity));  fornisce 1.879853862; la serie converge velocemente: da 1 a 20 abbiamo la somma 1.879853848. La convergenza deriva dal fatto che nn cresce molto più rapidamente di n! (vedi grafico a lato), cosa già vista nel primo modulo. Per provare rapidamente la convergenza della somma possiamo comunque usare il criterio del rapporto: an+1/an = (n+1)!nn/((n+1)n+1n!) = (n/(n+1))n = 1/(1+1/n)n → 1/e < 1.  Σn = h…∞ ((1+sin(n)) / n2) Vedi il punto 7 di questo documento  Σn = h…∞ ((5n+1) / (n3+5)) h = 0; da Maple il calcolo non viene svolto simbolicamente, ma numericamente sì:  evalf(sum((5*n+1)/(n^3+5), n=0..infinity));  fornisce 3.966781448; La convergenza deriva dal fatto che il termine via via sommato va a 0 come 1/n2 (vedi "limit comparison test").

•  Studia la convergenza di:
 ∑ _{n = 1..∞} (-1)ⁿ⁺¹ n / (10 n + 5)
Di fronte a questa serie Maple mi dà un messaggio come  1/15*hypergeom([2, 3/2],[5/2],-1)  o uno simile; se proviamo a calcolare la serie con  evalf  otteniamo un messaggio che ci fa capire che la serie diverge; per altro se sommiamo i primi 100 e i primi 101 termini otteniamo -0.02121266497 e 0.07829472419, se sommiamo i primi 1000 e i primi 1001 termini otteniamo -.002143520864 e 0.07851486625, che ci fanno capire che la serie non converge. La conferma teorica è semplice: il termine generico della serie non è un infinitesimo! (i termini pari e i termini dispari tendono -1/10 e a 1/10; se con Maple facessimo  limit ((-1)^(n+1)*n/(10*n+5),n=infinity);  otterremmo  −1/10..1/10  ad indicare questo fatto)
  (sotto il grafico del termine generico e quello della somma)
 
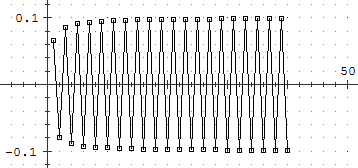
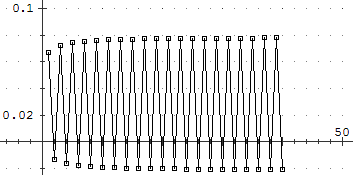
 ∑ _{n = 1..∞} cos(π n) / n²
Di fronte a questa serie Maple mi dà un messaggio come  hypergeom([1, 1, 1],[2, 2],-1)  o uno simile; se proviamo a calcolare la serie con  evalf  otteniamo -0.8224670334; le somme dei primi 20 e dei primi 21 termini sono -0.8212793783 e -0.8235469520, che ci fanno capire che la convegergenza è molto rapida. La convergenza è deducibile immediatamente dal fatto che il valore assoluto del termine è 1/n², e che quindi la serie dei valori assoluti converge. Ma bastava osservare che si tratta di una serie a segni alterni [cos(πn) oscilla tra −1 e 1] con il valore assoluto del termine n-esimo che tende a 0 decrescendo.
Per questo stesso motivo, ad es., ∑ _{n = 1..∞} cos(πn)/n e ∑ _{n = 1..∞} cos(πn)/√n convergono (pur non convergendo le serie dei loro valori assoluti).
 ∑ _{n = 3..∞} (-1)ⁿ / log(log(n))
Da Maple il calcolo non viene svolto simbolicamente, ma numericamente sì:  evalf(sum((-1)^n/ln(ln(n)), n=3..infinity));  fornisce -8.749551241; provando a fare la somma per vari valori si vede che la convergenza è abbastanza lenta. La convergenza è assicurata dal fatto che i segni dei termini si alternano e che il termine generico tende a 0.
•  Arrotondare ("a mano") a meno di 1/100  ∑ _{n = 0..∞} (-1)ⁿ / n!
Con Maple otterremmo subito che la serie vale 1/e, che potremmo valutare numericamente in 0.367879441171442, e da qui potremmo trovare il valore cercato (0.37); ma non è questo che vuole l'esercizio. A mano, eventualmente aiutandosi con Maple, con comandi come: sum((-1)^n/n!,n=0..0); sum((-1)^n/n!,n=1..1); sum((-1)^n/n!,n=2..2); …, possiamo trovare l'epressione iniziale del polinomio di Taylor: 1 − 1 + 1/2 − 1/6 + 1/24 − 1/120 + 1/720 …. È una serie a segni alterni coi termini via via sommati decrescenti in valore assoluto (vedi), e quindi l'errore che si commette approssimando la funzione con il polimonio a₀−a₁+…+(−1)ⁿa_n è pari ad a_n+1. Nel nostro caso 1/120 < 1/100, quindi 1−1+1/2−1/6+1/24 = 0.375 è l'approssimazione cercata. Se vogliamo una approssimazione a due cifre possiamo sicuramente prendere 0.37, in quanto il termine successivo del polinomio (−120) è negativo.