Soluzione agli "ulteriori esercizi"
Σn = 0…∞ 1/10n
1+0.1+0.01+0.001+… = 1.111… = 1 + 0.111… = 1 + 1/9 = 10/9. È uno
dei primi esempi di serie che si incontrano, nella scuola dell'obbligo ... (anche se non formulati in questo modo).
Σn = 0…∞ an/n!
È una generalizzazione di Σn = 0…∞ 1/n! che vale e. Con
Maple troveremmo che vale ea.
Possiamo dedurne la convergenza ad es. col criterio del rapporto:
simplify(a^(n+1)/(n+1)!/(a^n/n!)); dà a/(n+1)
che tende a 0, e che quindi, da un certo punto in poi, è minore di 1.
Σn = 1…∞ 1/(n+√n)
Maple non ci dà in alcun modo quanto vale questa somma. Con
evalf(sum(1/(n+sqrt(n)),n=1..3000));
e comandi analoghi troviamo che le somme dei primi 3000, 4000, 5000 e 6000 termini sono (approssimando)
9.213689266, 9.499828464, 9.721918769 e 9.903462676. La serie sembra non avere limite finito (ogni 1000
tende a crescere di circa 0.2). La conferma teorica è semplice: 1/(n+√n)
è un infinitesimo (per n → ∞) dello stesso ordine di 1/n e
Σn = 1…∞ 1/n diverge.
Σn = 2…∞ 1/(n·ln(n))
Il modo forse più semplice per studiare questa serie è ricorrere al test integrale:
∫1/(x·ln(x)) dx vale ln(ln(x)) (+C),
quindi ∫ [2,n] 1/(x·ln(x)) dx
si comporta come ln(ln(n)) − vale ln(ln(n))−ln(ln(2)) − che tende all'infinito.
Quindi la serie diverge. Lo studio sperimentale non darebbe conclusioni facilmente interpretabili in quanto si tratta
di una serie che diverge molto lentamente. La conferma di questa lentezza è data dal contenuto della nota seguente.
Nota. Osserviamo che ∫1/(x·ln(x)s) dx per
s > 1 vale
− ln(x)1−s / (s-1) =
−1 / (ln(x)s−1(s-1)) (+C), e
dunque ∫ [2,n] 1/(x·ln(x)s) dx
per n → ∞ tende ad un valore finito (in quanto −1/(ln(n)s−1(s-1))
tende a 0). Quindi la serie Σn = 2…∞ 1/(n·ln(n)s)
converge.
Σn = 2…∞ 1/ln(n!)
Con
evalf(sum(1/ln(n!),n=1..100));
e comandi analoghi troviamo che le somme dei primi 100, 200, 400, 800 e 1600 termini sono (approssimando)
3.962852697, 4.136813545, 4.285551649, 4.415263811 e 4.530179957 (al raddoppiare del numero
degli addendi la differenza delle uscite scende molto lentamente). Dalle uscite numeriche
non capiamo quello che accade. Teoricamente, se ricordiamo che nn cresce più
rapidamente di n!, o anche solo che, da un certo punto in poi, nn > n!,
possiamo concludere che la serie diverge, per quanto trovato nell'esercizio precedente.
Infatti log(nn) = n·log(n) > 0 e, quindi,
da un certo n in poi, 1/log(n!) > 1/(n·log(n)) > 0 (quindi per
il test del confronto …).
Σn = 1…∞ (√(n+1) − √n)3
Con Maple, con evalf, ho immediatamente la convergenza a 0.247317349864127... Valutiamo la
cosa teoricamente. Innanzi tutto osserviamo che (√(n+1) − √n)3
→ 0 per n → ∞ in quanto √(n+1)−√n → 0:
√(n+1)−√n =
(√(n+1)−√n)(√(n+1)+√n)/(√(n+1)+√n) =
(n+1−n)/(√(n+1)+√n) = 1/(√(n+1)+√n) → 0.
Nel far questo abbiamo anche visto che (√(n+1) − √n)3 = 1/(√(n+1)+√n)3.
Abbiamo, dunque, che il termine generico della nostra serie va a 0 come 1/n3/2, 3/2 > 1, quindi
la serie converge.
Σn = 1…∞ (−1)n ln(n) / n!
Con Maple, con evalf, ho immediatamente la convergenza a 0.20997038389801... Valutiamo la
cosa teoricamente. Innanzi tutto osserviamo che si tratta di una serie a segni alterni. Vediamo prima che cosa accade
per Σn = 1…∞ (−1)n ln(n) / n.
Con Maple abbiamo che anche questa converge (a 0.15986890374243...). La dimostrazione è facile: basta
far vedere che ln(n)/n tende a 0 decrescendo da un certo n in poi. Dx(ln(x)/x)
= (1−ln(x))/x2 < 0 per x > e; OK.
Quindi questa seconda serie converge e, a maggior ragione, dato che ln(n)/n! < ln(n)/n,
converge anche la prima.
Σn = 1…∞ ln(n) / n!
Con Maple, con evalf, ho immediatamente la convergenza a 0.60378286279148...
La presenza del fattoriale ci suggerisce di procedere col metodo del rapporto:
(ln(n+1)/(n+1)!) / (ln(n)/n!) = (ln(n+1)/(n+1)) / ln(n) che tende a 0 (tende a comportarsi come 1/n),
e quindi, da un certo punto in poi, è sicuramente minore di 1.
Σn = 2…∞ n / C(n,2)
Σn = 2…∞ n / C(n,2) = Σn = 2…∞ n / (n·(n−1)/2)
= Σn = 2…∞ 2 / (n−1) che diverge (in quanto 2/(n−1) va a 0 come 1/n).
Σn = 3…∞ n / C(n,3)
Σn = 3…∞ n / C(n,3) =
Σn = 3…∞ n / (n(n−1)(n−2)/6)
= Σn = 3…∞ 6 / ((n−1)(n−2)) che converge
(in quanto 6/((n−1)(n−2)) va a 0 come 1/n2).
Con Maple (sum(n/binomial(n, 3),n=3..infinity);)
ho che la serie vale 6.
Σn = 1…∞ sin(1/n)
Per x → 0 sin(x) ≈ x, quindi per n → ∞ sin(1/n) ≈ 1/n. Dunque
la serie diverge.
| Del resto |
F(x)=SIN(1/x)
[1,10] F SUM = 2.737823151
[1,100] F SUM = 4.995486683
[1,1000] F SUM = 7.293571858
[1,10000] F SUM = 9.595706951
[1,100000] F SUM = 11.89824704 |
Σn =
1…∞ (−1)n (n+1) / (n2+100)
Con Maple, con evalf, ho immediatamente la convergenza a -0.00751276150427223...
Lo stesso posso averlo con Poligon:
F(x)=(-1)^x*(x+1)/(x^2+100)
[1,100] F SUM = -0.002537512803
[1,1000] F SUM = -0.007012561974
[1,10000] F SUM = -0.007462759055
[1,100000] F SUM = -0.007507761479
Ecco il grafico (parziale) della serie:
F(x)=(-1)^x*(x+1)/(x^2+100)
#T=300
N
noscrivi=1
FOR #N=1 TO #T : #S=[1,#N] F SUM ; PLOT X:#N Y:#S
noscrivi=0
oo
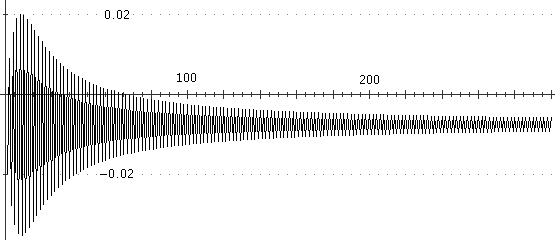
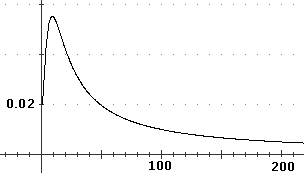
La conclusione della convergenza delle serie è deducibile dal fatto che il valore assoluto
del termine n-esimo G(x) (di cui sotto è parzialmente tracciato il grafico) da un certo
punto in poi (per x ≥ √101−1) decresce.
G(x) = (x+1)/(x^2+100)
Σn =
1…∞ (n+1) / (n2+100)
Con Maple, con evalf, ho immediatamente la divergenza a ∞
G(x) = (x+1)/(x^2+100)
[1,100] G SUM = 2.453830604
[1,1000] G SUM = 4.755966045
[1,10000] G SUM = 7.058951245
[1,100000] G SUM = 9.361580839
A questa conclusione di può arrivare teoricamente tenendo conto che il termine
n-esimo è positivo e tende a 0 come 1/n.
Σn =
1…∞ n·sin(a)n−1
Con Maple (sum(n*sin(a)^(n-1), n=1..infinity);)
ho che la serie vale 1/(1−sin(a))2.
Ma questo vale se, ovviamente, sin(a) ≠ 1 (altrimenti la
serie, ovviamente, diverge).
Verifiche, ad es., con Poligon:
F(x)=x*SIN(#A)^(x-1)
#A=30*GR
[1,100] F SUM = 4
[1,101] F SUM = 4
#A=PI/2
[1,100] F SUM = 5050
[1,1000] F SUM = 500500
#A=60*GR
[1,400] F SUM = 55.71281292
[1,401] F SUM = 55.71281292
#A=225*GR
[1,100] F SUM = 0.3431457505
[1,101] F SUM = 0.3431457505
#B=1/(1-SIN(#A))^2
#A=30*GR
#B=4
#A=60*GR
#B=55.71281292110199
#A=225*GR
#B=0.3431457505076198
Che la serie (= 1+2sin(a)+3sin(a)2+…) converga può essere
concluso in base al criterio del rapporto:
(n+1)·sin(a)n / (n·sin(a)n−1)
= sin(a)·(n+1)/n → sin(a)
Σn =
1…∞ (√(1+n2) − n)
Le uscite numeriche ci suggeriscono che la serie diverga: il termine n-esimo
sembra andare a 0 come 1/n (al raddoppiare di n il valore tende a dimezzarsi):
F(x) = SQR(x^2+1)-x
F(100)/F(50) = 0.5000374943761793
F(200)/F(100) = 0.5000093746477777
F(400)/F(200) = 0.5000023437313356
La cosa è facile da dimostrare (abbiamo già più volte usato il "trucco" seguente):
√(1+n2) − n = ((√(1+n2)−n) ((√(1+n2)+n) /
((√(1+n2)+n) =
1 / ((√(1+n2)+n) ≈ 1 / 2n
Σn =
1…∞ 1/n1+1/n
Le uscite numeriche ci suggeriscono che la serie diverga: il termine n-esimo
sembra andare a 0 come 1/n (al raddoppiare di n il valore tende a dimezzarsi):
F(x) = 1/x^(1+1/x)
[1,50] F SUM = 3.76589169
[1,100] F SUM = 4.413685353
[1,200] F SUM = 5.08037843
[1,400] F SUM = 5.75845537
[1,800] F SUM = 6.443164205
F(200)/F(100) = 0.5098763337386893
F(400)/F(200) = 0.5057897271299492
F(800)/F(400) = 0.5033224382926408
Maple può confermarci questa conclusione:
limit((1/n)/(1/n^(1+1/n)), n=infinity); dà proprio 1.
Il calcolo è effettuabile a mano facilmente:
(1/n) / (1/n^(1+1/n)) = n^(1/n) = n√n → 1 (cosa nota, ma comunque affrontabile
riscrivendo il termine come
exp(log(n^(1/n)) = exp(log(n)/n), che tende a exp(0) = 1.
Σn =
0…∞
(√(1+na) − √(na))
Per a=2 abbiamo già visto (due esercizi sopra) che la serie diverge.
A maggior ragione la serie diverge per a<2 (il termine n-esimo va a 0 più lentamente).
Per a>2 le uscite sembrano suggerirci che la serie converga:
il termine n-esimo sembra andare a 0 più velocemente di 1/n:
F(x) = SQR(x^#A+1)-SQR(x^#A)
#A = 2.5
F(200)/F(100) = 0.4204490729037894
F(400)/F(200) = 0.4204483606745886
F(800)/F(400) = 0.4204482359154465
Anche in questo caso la cosa è facile da dimostrare:
√(1+na) − √(na) =
((√(1+na)−√(na))
((√(1+na)+√(na)) / ((√(1+na)+√(na)) =
1 / ((√(1+na)+√(na)) ≈ 1 / 2na/2

