Soluzione degli esercizi 
Primo foglio
(1)  Calcola  ∑ _n=1..∞ 1/((n+x)(n+x+1)(n+x+2))  con Maple, ed esprimi il risultato usando il comando "factor". Il risultato ottenuto vale per ogni intero x? Prova a dimostrare quanto ottenuto usando la proprietà telescopica.
Con Maple:
> Sum(1/((n+x)*(n+x+1)*(n+x+2)),n=1..infinity) = sum(1/((n+x)*(n+x+1)*(n+x+2)),n=1..infinity);
∑ _n=1..∞ 1/((n+x)(n+x+1)(n+x+2)) = 1/(2·(2+3x+x²))
> factor(sum(1/((n+x)*(n+x+1)*(n+x+2)),n=1..infinity));
1/(2(x+2)(x+1))
"A mano":
1/((n+x)(n+x+1)(n+x+2)) = ( 1/((n+x)(n+x+1)) − 1/((n+x+1)(n+x+2)) ) / 2
Quindi si tratta di una serie telescopica, che converge ad a₁−L dove a_n è 1/(2(n+x)(n+x+1)) e L è il limite degli a_n, ossia a 1/(2(x+2)(x+1)).
(Nota: ogni serie ∑b_i può essere messa in forma telescopica [basta considerare la serie a_n+1 = a₁−(b₁+...+b_n), a₁ qualunque], ma solo in alcuni casi la cosa è utile)
Con Maple si può controllare che si ottiene una somma per ogni x intero non negativo, mentre non si ottiene risultato per x negativo (infatti i temini della somma sono in alcuni casi non definiti). La dimostrazione precedente vale per ogni x intero non negativo.

(2)  Confronta la convergenza delle serie: 1+1/2+1/4+1/8+1/16+...  e  1+1−1/2+1−3/4+1−7/8+1−15/16+...
Attenzione, per quanto 1+1/2 = 1+1−1/2, 1+1/2+1/4 = 1+1−1/2+1−3/4, … le due serie non sono equivalenti in quanto la seconda oscilla tra 1 e 1+1, tra 1+1−1/2 e 1+1−1/2+1, tra 1+1−1/2+1−3/4 e 1+1−1/2+1−3/4+1, …: le somme di posto dispari tendono a 2, quelle di posto pari a 3. Questo esempio illustra una importante differenza tra le somme finite e quelle infinite: 1+1−1/2+1−3/4+1−7/8+1−15/16+... non equivale a 1+(1−1/2)+(1−3/4)+(1−7/8)+(1−15/16)+...

(3)  Trova con Maple ∑ _n=0..∞ xⁿ,  ∑ _n=0..∞ x²ⁿ,  ∑ _n=0..∞ x²ⁿ⁺¹,  ∑ _n=0..∞ (−x)ⁿ,  ∑ _n=0..∞ (−x²)ⁿ,  ∑ _n=0..∞ (−1)ⁿx²ⁿ⁺¹,  ∑ _n=0..∞ (4x²)ⁿ,  cerca di confermare quanto trovato con qualche ragionamento teorico (e stabilisci per quali x le eguaglianze trovate valgono).
• È noto che ∑ _n=0..∞ xⁿ = 1/(1−x) converge solo per |x| < 1 (per x=1/2 è la prima serie dell'es. precedente)
• ∑ _n=0..∞ x²ⁿ è costituita dai termini della precedente serie con esponente pari, ma posso ottenerla anche rimpiazando x con x².
Quindi converge a 1/(1−x²) per |x| < 1.
• ∑ _n=0..∞ x²ⁿ⁺¹ la ottengo dalla precedente moltpilcandone i termini per x, quindi converge a x/(1−x²) per |x| < 1.
• ∑ _n=0..∞ (−x)ⁿ la ottengo da ∑ _n=0..∞ xⁿ rimpiazzando x con −x:  ∑ _n=0..∞ (−x)ⁿ = 1/(1+x) per |x| < 1.
• ∑ _n=0..∞ (−x²)ⁿ la ottengo dalla precedente rimpiazzando x con x²: 1/(1+x²) per |x| < 1.
• ∑ _n=0..∞ (−1)ⁿx²ⁿ⁺¹ la ottengo dalla precedente moltiplicando per x:  x/(1+x²) per |x| < 1 (nota: (−x²)ⁿ = (−1)ⁿx²ⁿ)
• ∑ _n=0..∞ (4x²)ⁿ la ottengo da ∑ _n=0..∞ x²ⁿ rimpiazzando x con 2x:  converge a 1/(1−4x²) per |2x| < 1, ossia per |x| < 0.5.
  Tutte le somme (non dove esse valgono) possono essere trovate immediatamente con Maple.

(4)  Differenziando e integrando la serie geometrica (e l'espressione che ne esprime il valore) si ha:
∑ _n=0..∞ nxⁿ⁻¹ = …
∑ _n=0..∞ (−1)ⁿx²ⁿ⁺¹/(n+1) = …
Per quali x valgono queste eguaglianze?
Si tratta di serie di potenze. Quindi:
∑ _n=0..∞ nxⁿ⁻¹ = 1/(1−x)² se |x| < 1; ho derivato, rispetto ad x, 1/(1-x)
∑ _n=0..∞ (−1)ⁿx²ⁿ⁺¹/(n+1) = log(1+x); vale se |x| < 1, ma anche se x = 1 − ∑ _n=0..∞ (−1)ⁿ/(n+1)) = log(2).


(5)  Integrando ∑ _n=0..∞ (−x²)ⁿ = 1/(x²+1) si trova ...
(attenzione: Maple potrebbe darti una somma "strana"). Per quali x vale questa eguaglianza?
x − x³/3 + x⁵/5 − x⁷/7 + … = arctan(x). La serie sicuramente converge per |x| < 1, dove converge la serie di partenza.
La serie converge anche per |x| = 1:
sum((-1)^n/(2*n+1),n=0..infinity);   e   sum(-(-1)^n/(2*n+1),n=0..infinity);   convergono a π/4 e −π/4 (le arcotangenti di 1 e −1).
Per |x| > 1 la serie diverge (la somma oscilla tra valori che tendono a ∞ e a −∞).
Verifica:   taylor(arctan(x),x,8);   dà   x − x³/3 + x⁵/5 − x⁷/7 + O(x⁹) (vedi)

Secondo foglio
(1)  Usando la formula di MacLaurin del 3° ordine, approssima e^0.1+sin(0.1) e maggiora il valore assoluto dell'errore commesso, e precisa il segno dell'errore.
exp(x) = 1 + x + x²/2 + x³/3! + exp(c1) x⁴/4!   con c1 tra 0 ed x
sin(x) = x − x³/3! + cos(c2) x⁵/5!   con c2 tra 0 ed x
exp(x) + sin(x) = 1 + 2x + x²/2 + exp(c1) x⁴/4! + cos(c2) x⁵/5!   con c1 e c2 tra 0 ed x
exp(0.1) + sin(0.1) ≈ 1 + 0.2 + 0.1²/2 = 1.205
Sia E l'errore. E = exp(c1) 0.1⁴/4! + cos(c2) 0.1⁵/5!   con c1 e c2 tra 0 ed 0.1. Quindi E > 0, ossia 1.205 è una approssimazione per difetto del valore cercato.
E < 3/(10⁴·24) + 1/(10⁵·120) = 1.258333…·10⁻⁵ < 0.000013

(2)  Determina l'insieme degli x per cui la serie data converge e calcolane la somma:
(a) ∑ _n=0..∞ (−1)ⁿ x²ⁿ     |x| < 1;  1/(1+x²)  −  da ∑ _n=0..∞ (−1)ⁿ xⁿ rimpiazzando x con x²
(b) ∑ _n=0..∞ xⁿ / 3ⁿ⁺¹     |x| < 3;  1/(3−x)  −  xⁿ/3ⁿ⁺¹ = (x/3)ⁿ/3
(c) ∑ _n=0..∞ n xⁿ     |x| < 1;  x/(1−x)²  −  da ∑ _n=0..∞ xⁿ = 1/(1−x), derivando e poi moltiplicando per x …
(d) ∑ _n=0..∞ (−1)ⁿ n xⁿ     |x| < 1;  −x/(1+x)²  −  dalla precedente rimpiazzando x con −x
(e) ∑ _n=0..∞ (−2)ⁿ (n+2)/(n+1)·xⁿ     |x| < 1/2;  1/(1+2x) + log(1+2x)/(2x)   [vedi, sotto, i commenti]
(f) ∑ _n=1..∞ 2ⁿ xⁿ / n     −1/2 ≤ x < 1/2;  −log(1−2x)  −  dallo sviluppo di log(1+x) ricavo quello di log(1-x); usando questo, e riscrivendo 2ⁿxⁿ come (2x)ⁿ …
(g) ∑ _n=0..∞ (−1)ⁿ / (2n+1)·(x/2)²ⁿ     −2 ≤ x ≤ 2;  2/x·arctan(x/2)
Con Maple si ottiene un'espressione equivalente alla soluzione se si opera in C. Per trovare la soluzione direttamente occorre svolgere, direttamente, il calcolo:
ricordare che (vedi) ∑ _n=0..∞ (−1)ⁿ / (2n+1)·x²ⁿ⁺¹ = arctan(x), dedurne che ∑ _n=0..∞ (−1)ⁿ / (2n+1)·x²ⁿ = arctan(x)/x, e quindi che ∑ _n=0..∞ (−1)ⁿ / (2n+1)·(x/2)²ⁿ = arctan(x/2)·2/x. Possiamo verificare la cosa con Maple calcolando  taylor(arctan(x/2)*2/x, x);.
(h) ∑ _n=0..∞ (−1)ⁿ x³ⁿ/n!     ogni x;  exp(−x³)
∑ _n=0..∞ xⁿ/n! = exp(x),  ∑ _n=0..∞ (−1)ⁿ xⁿ/n! = exp(-x),  ∑ _n=0..∞ (−1)ⁿ x³ⁿ/n! = exp(-x³)
(i) ∑ _n=0..∞ xⁿ / (n+3)!     ogni x;  x⁻³(exp(x)−1−x−x²/2) se x ≠ 0, 0 se x = 0
(usa  simplify(expand(sum(x^n/(n+3)!,n=0..infinity)));  se vuoi riscrivere l'espressione che ti fornisce Maple;
in ogni caso basta consoscere lo sviluppo di exp(x), e osservare che la serie data si ottiene da questo saltando i primi tre termini e dividendo per x³)
(j) ∑ _n=0..∞ (x−1)ⁿ / (n+2)!     ogni x;  (exp(x−1)−x)/(x−1)² se x ≠ 1, 1/2 se x = 1
(usa  simplify(expand(...));  se vuoi riscrivere l'espressione che ti fornisce Maple)
[traccia: ∑ _n=0..∞ xⁿ/n! → ∑ _n=0..∞ xⁿ/(n+2)! → ∑ _n=0..∞ (x−1)ⁿ/(n+2)!]
(k) ∑ _n=0..∞ xⁿ / 2ⁿ⁺¹     |x| < 2;  1/(2−x)
(l) ∑ _n=0..∞ x²ⁿ⁺¹ / (2n+1)!     ogni x;   sinh(x) (vedi)
[per l'es. (e) con Maple si ottiene una soluzione strana: ln(1+2x)/x−hypergeom([2, 2],[3],-2x)x; di fronte ad altre espressioni simili - come  hypergeom([2, 2],[2,3],-2*x); - Maple fornisce una versione esplicita; con Maple-8 e successivi il comando  convert( hypergeom([2, 2],[3],-2*x), StandardFunctions);  fornisce -1/(x*(2*x+1))+1/2*1/x^2*ln(2*x+1) il che consente di arrivare ad una soluzione equivalente a quella qui proposta; in ogni caso con  plot (x->sum((-2)^n*(n+2)/(n+1)*x^n,n=0..infinity),-1..1);  si ottiene il grafico seguente:
   
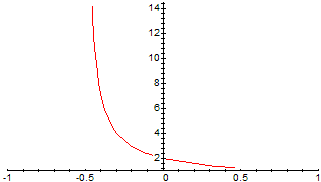
che consente di capire che la serie converge per |x|<1/2, e che è incerto che cosa accade per x = 1/2;  procedendo "a mano", comunque, si ottiene:
∑ _n=0..∞ (−2)ⁿ (n+2)/(n+1)·xⁿ = ∑ _n=0..∞ (−1)ⁿ (n+2)/(n+1)·(2x)ⁿ che converge dove converge ∑ _n=0..∞ (−1)ⁿ (2x)ⁿ, ossia (vedi es. 9) per |x| < 1/2; per trovare il valore della somma scriviamo (n+2)/(n+1) come 1+1/(n+1) e ci ricondiciamo a ∑ _n=0..∞ (−2)ⁿ xⁿ + ∑ _n=0..∞ (−2)ⁿ xⁿ/(n+1) = 1/(1+2x) + ln(1+2x)/(2x) (come possiamo verificare anche con Maple)]
(3)  Provare a studiare con Maple le serie considerate negli esempi del paragrafo "serie di funzioni".
Es. 1.  Sum((-1)^n*x^(3*n)/((n+1)*4^n),n=0..infinity);
Per controllare la risposta posso fare: sum((-1)^n*x^(3*n)/((n+1)*4^n),n=0..0);  sum((-1)^n*x^(3*n)/((n+1)*4^n),n=1..1);  sum((-1)^n*x^(3*n)/((n+1)*4^n),n=2..2);  …
Con "simplify" (e la "sum" con la "s" minuscola) ottengo anche la somma -4*(2*ln(2)-ln(4+x^3))/x^3.
Es. 2.  Sum(x^(2*n+1)*(-1)^n/(2*n+1),n=0..infinity);
controllo: sum((-1)^n*x^(3*n)/((n+1)*4^n),n=0..0);  sum((-1)^n*x^(3*n)/((n+1)*4^n),n=1..1); …
Con  taylor(arctan(x),x,10);  ottengo: x - x^3/3 + x^5/5 - x^7/7 + x^9/9 + O(x^10)
Es. 3.  Sum(x^n*(n+2)/n!,n=0..infinity);  Con la "s" minuscola ottengo proprio (x+2)exp(x)
Es. 4.  In questo caso ci limitiamo a ritrovare lo stesso valore;   taylor(exp(x)*ln(1+x),x,7);  fornisce proprio x + 1/2 x^2 + 1/3 x^3 + 3/40 x^5 - 7/144 x^6 + O(x^7)
Es. 5.  taylor(tan(x),x,8);   fornisce   x + x^3/3 + 2/15*x^5 + 17/315*x^7 + O(x^9)
Es. 6.  Per sviluppare (con Maple) in serie di potenze di x-1 mi conviene fare una sostituzione:
con  subs(x=u+1, 1/(2+x));   ottengo   1/(u+3)
con  taylor(1/(u+3),u);   ottengo   1/3-1/9u+1/27u^2-1/81u^3+1/243u^4-1/729u^5+O(u^6)
con  subs(u=x-1, convert(taylor(1/(u+3),u),polynom));   (o subs(u=x-1, 1/3- ... -1/729u^5);) ottengo   4/9-x/9+(x-1)^2/27-(x-1)^3/81+(x-1)^4/243-(x-1)^5/729
Es. 7.  Maple di fronte a  sum(-(x^n)/(n+1),n=0..infinity);  fornisce subito  ln(1-x)/x  ed anche di fronte a  taylor(log(1-x)/x,x);  fornisce  -1-x/2-x^2/3-x^3/4-x^4/5+O(x^5)
Es. 9.  Maple di fronte a  sum((n+2)*(n+1)/2*x^n,n=0..infinity);  fornisce   1/(1-x)^3  e di fronte a  taylor(1/(1-x)^3,x);  fornisce  1 + 3*x+6*x^2 + 10*x^3 + 15*x^4 + 21*x^5 + O(x^6)