• Vedi esercizio 1 (e soluzione)

In un linguaggio di programmazione Σ_n=0…10 n² può essere realizzato con un cliclo che (ad es. in un Basic strutturato) può avere l'espressione seguente:

S = 0 FOR N=0 TO 10 : S = S+N^2 : NEXT PRINT S

In Poligon avrebbe una forma simile:

#S = 0 _ FOR #N=0 TO 10 : #S = val(#S+#N^2)

[vedi QUI e QUI per i cicli FOR e QUI per l'uso di "_"; occorre mettere VAL(...) in quanto (VEDI) Poligon nelle variabili #V memorizza termini, non valori numerici: se usassi #S = #S+#N^2, in #S verrebbe memorizzata l'espressione #S+#N^2 e di fronte al calcolo di #S il computer entrerebbe in loop]
  Se poi aziono  #S=  ottengo il valore della somma.  In Poligon c'è un modo più semplice per realizzare le somme (VEDI). Ad esempio nel caso precedente posso fare:

F(x) = x^2 [0,10] F SUM

Poligon calcola la somma F(0)+F(1)+...F(10), ossia la somma degli F(x) estesa a tutti gli interi x che stanno nell'intervallo [0,10].

• Vedi esercizio 4 (e soluzione)

• Vediamo come studiare la serie 1-1/2+1/3-1/4+... che prosegue sommando i numeri "a segni alterni" (ossia ciascuno di segno opposto rispetto al precedente) aventi come valore assoluto i reciproci degli altri numeri naturali. Devo cercare di esprimere il termine generico della somma come funzione dell'indice. Se voglio che F(1)=1, F(2)=-1/2, F(3)=1/3, ... posso fare:

F(x) = (-1)^(x+1)/x

Poi sperimentalmente studio Σ_n=1…∞ F(n)

[1,1] F SUM = 1 [1,2] F SUM = 1/2 [1,3] F SUM = 5/6 [1,4] F SUM = 7/12 [1,5] F SUM = 47/60 [1,10] F SUM = 1627/2520 [1,100] F SUM = 0.6881721793 [1,1000] F SUM = 0.6926474306 [1,10000] F SUM = 0.6930971831 [1,100000] F SUM = 0.6931421806

Mi fermo in quanto il programma impiega troppo tempo, ma sembra di poter congetturare che la serie converga a un numero compreso tra 0.69 e 0.7.

[ in QBasic avrei potuto usare il programma:
DEFDBL A-Z
s = 0
FOR N = 1 TO 100000: s = s + (-1) ^ (N + 1) / N
IF N \ 10000 = N / 10000 THEN PRINT N, s
NEXT
(la prima riga serve per far operare su numeri rappresentati con una doppia quantità di bit; la quarta per stampare le uscite quando N è un multiplo di 10000)
ottenendo:
10000   .6930971830599594
20000   .6931221811849594
30000   .6931305141710715
40000   .6931346807162136
50000   .6931371806599679
60000   .693138847296085
70000   .6931400377538591
80000   .6931409305990451
90000   .6931416250352912
100000  .693142180584982 ]

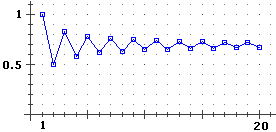
Per capire meglio l'andamento posso rappresentare graficamente la successione (cioè la somma parziale di ordine n in funzione di n). In Poligon posso procedere così (se voglio far variare n da 1 a 20):

N _ FOR #N = 1 TO 20: #S = [1,#N] F SUM; PLOT x:#N y:#S

Ottengo:      
per vedere tutto il grafico faccio un doppio clic su [o] e poi eventualmente opero uno zoom con [-y] e uno spostamento con [<];
con [:] posso evidenziare i punti;  potrei scalare il grafico anche con  scala sx:-1..25 sy:-0.2..1.2

Con Maple posso avere l'espressione     simbolica della somma:

sum((-1)^(x+1)/x, x=1..infinity);    ln(2) evalf(sum((-1)^(x+1)/x, x=1..infinity), 30);   .693147180559945309417232121458

• Analogamente posso studiare Σ_{n = 1…∞} (-1)ⁿ⁺¹(n+10)/(5n):

F(x) = (-1)^(x+1)*(x+10)/(5x) [1,1] F SUM = 11/5 [1,2] F SUM = 1 [1,5] F SUM = 53/30 [1,10] F SUM = 1627/1260 [1,100] F SUM = 1.376344359 [1,1000] F SUM = 1.385294861 [1,10000] F SUM = 1.386194366

Sembra che la somma converga, ma facciamo il grafico: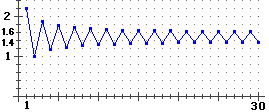

    Avendo scelto un intervallo abbastanza ampio si intuisce che le somme di ordine pari e quelle di ordine dispari tendono a stabilizzarsi su due valori diversi. Siamo stati ingannati dall'aver, da un certo punto in poi, calcolato solo somme di ordine pari. Rimediamo:

[1,99] F SUM = 1.596344359 [1,999] F SUM = 1.587294861 [1,9999] F SUM = 1.586394366

    Si può congetturare che la sottosuccessione delle somme di ordine pari e quella delle somme di ordine dispari convergano a due valori diversi (circa 1.39 e 1.59).
•  La sperimentazione al calcolatore è di aiuto a capire che cosa accade, ma va effettuata non alla cieca, e occorre cercare di accompagnata da conferme teoriche.
    Nel nostro caso quanto accade nel primo esempio possiamo interpretarlo col fatto che le due sottosuccessioni delle somme di ordine pari e di ordine dispari sono una crescente e l'altra decrescente (nel primo caso, passando dal posto 2N al posto 2N+2 aggiungo 1/(2N+1)-1/(2N+2) che è positivo in quanto 2N+2>2N+1; nel secondo caso, passando dal posto 2N+1 al posto 2N+3 aggiungo -1/(2N+2)+1/(2N+3) che è negativo in quanto 2N+3>2N+2) e limitate, per cui convergono una al suo estremo superiore e l'altra al suo estremo inferiore, e che questi due estremi devono coincidere in quanto tra una somma di posto pari N e quella di posto dispari successivo N+1 la differenza è 1/(N+1) che tende a 0. Questa argomentazione, in pratica, è la stessa che dimostra il teorema (noto come criterio di Leibniz):

una serie a segni alterni i valori assoluti dei cui termini formino una successione decrescente e tendente a 0 converge.

    Nel secondo esempio, invece, le due sottosuccessioni (quella dei posti pari e quella dei posti dispari) sono sì una crescente e l'altra decrescente, ma la distanza tra l'una e l'altra non tende ad azzerarsi: tra una somma di posto pari N e quella di posto dispari successivo la differenza è il valore assoluto del termine N+1-esimo, ossia (N+1+5)/(5N+5), che tende decrescendo a 1/5 = 0.2, come avevamo visto anche con la sperimentazione numerica, non a 0.  In pratica la serie è una successione che oscilla tra due valori che distano più di 1/2 e non può convergere: posto ε = 1/2, comunque prenda L e comunque prenda N posso trovare N > N tale che la somma di ordine N disti da L più di ε.
    Potevo concludere la divergenza della seconda serie anche osservando che se la serie Σ_{n = 0…∞} a(n) converge, allora a(n) → 0,  e tenendo conto che nel nostro caso (n+10)/(5n) → 1/5 ≠ 0.

Con Maple:

sum( (-1)^(x+1)*(x+10)/(5*x), x=1..infinity);   11/5*ln(2)-1/10*hypergeom([2, 2],[3],-1)     o  undefined evalf(");     o     evalf(%);   Error, (in evalf/hypergeom/converg) series is divergent

•  Σ_{n = 0…∞} (3ⁿ+4ⁿ)/5ⁿ è una serie a termini positivi, quindi è una successione crescente.

F(X) = (3^x+4^x)/5^x [0,10] F SUM = 7.061433344 [0,100] F SUM = 7.499999999 [0,200] F SUM = 15/2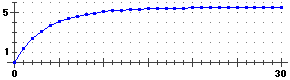

Si è stabilizzata; [0,500] F SUM   non dà valori (5^x per x così grande da luogo a un overflow).
Cerchiamo una giustificazione teorica. Idea:
Σ_{n = 0…k} (3ⁿ+4ⁿ)/5ⁿ = Σ_{n = 0…k} 3ⁿ/5ⁿ + Σ_{n = 0…k} 4ⁿ/5ⁿ [distribuendo "/5", riordinando la somma,raccogliendo "/5"]
Σ_{n = 0…k} 3ⁿ/5ⁿ = Σ_{n = 0…k} (3/5)ⁿ = (1-(3/5)ⁿ)/(1-3/5) → 1/(1-3/5) = 5/(5-3) = 5/2
Σ_{n = 0…k} 4ⁿ/4ⁿ = Σ_{n = 0…k} (4/5)ⁿ = (1-(4/5)ⁿ)/(1-3/5) → 1/(1-4/5) = 5
Quindi Σ_{n = 0…k} (3ⁿ+4ⁿ)/5ⁿ → 5/2+5 = 15/2
  Potevamo arrivare a questa conclusione anche usando:
  • se Σ_{n = h…∞} a(n) = A e Σ_{n = h…∞} b(n) = B, allora Σ_{n = h…∞} (a(n)+b(n)) = A+B
  • Σ_{n = 0…∞} pⁿ = 1/(1-p) se |p|<1, diverge a ∞ se p≥1, diverge se p≤-1 [serie geometrica].

Con Maple:

sum( (3^n+4^n)/5^n, n=0..infinity);   15/2

•  6/√3 - 6/3/(√3)³ + 6/5/(√3)⁵ + …   e così via alternando i segni e aumentando di 2 denominatore ed esponente.

F(X) = (-1)^(x+1)*6/(2*x-1)/(SQR(3)^(2*x-1)) [1,10] F SUM = 3.14159051093808 [1,30] F SUM = 3.14159265358979 [1,31] F SUM = 3.14159265358979

[nota: è facile ma non è banale passare dall'elencazione di un po' di termini ad un'espressione che li sintetizzi come (-1)^(x+1)*6/(2*x-1)/(SQR(3)^(2*x-1))]

Che la serie converga è confermato dal fatto che si tratta di una serie a segni alterni con termine n-esimo, 6/(2n-1)/n^(2n-1)/2, che tende a 0 decrescendo. Sembra che converga a π. Confrontiamo col valore di π:  pi = 3.14159265358979. OK.
Al momento non abbiamo gli strumenti per dimostrare che la somma è effettivamente π. La determinazione dello sviluppo decimale di π e di altri numeri irrazionali è stata una delle molle che hanno spinto allo studio delle serie.

Con Maple:	sum( (-1)^(n+1)*6/(2*n-1)/(sqrt(3)^(2*n-1)), n=1..infinity);   2*3^(1/2)*hypergeom([1/2, 1],[3/2],-1/3)     o   ... evalf(");   evalf(%);   3.141592654
o otteniamo qualcosa in cui compare       l'untità immaginaria (I in Maple) con peso "trascurabile":	evalf(", 15);   evalf(%, 15);   3.14159265358980 - .915000000000000*10^-15*I evalf(", 20);   evalf(%, 20);   3.1415926535897932383 + .16634605591076231057*10^-19*I

Esercizi (provare a farli; poi vedremo le soluzioni)
• Studia la serie  Σ_{n = 1…∞} 1 / (n(n+1)) sperimentalmente, congettura il valore della somma, e prova a dimostrare che converge a questo valore (idea: in base alle uscite congettura l'espressione del valore della somma di ordine n in funzione di n, dimostra che la somma ha effettivamente questa espressione, e poi studiane il limite per n →∞).
• Studia la convergenza delle seguenti serie, prendendo, caso per caso, come h il numero naturale più piccolo per cui tutti i termini della serie sono definiti:
Σ_{n = h…∞} (1 / log(n))     Σ_{n = h…∞} (1 / (1+√n))     Σ_{n = h…∞} ((2n)! / (n!)²)
Σ_{n = h…∞} (2ⁿ⁺¹ / nⁿ)     Σ_{n = h…∞} (cos(nπ) / log(n))     Σ_{n = h…∞} ((n)! / nⁿ)
Σ_{n = h…∞} ((1+sin(n)) / n²)     Σ_{n = h…∞} ((5n+1) / (n³+5))