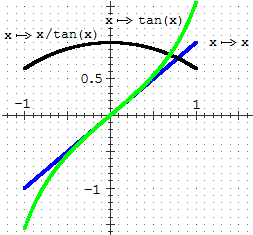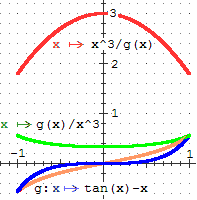Richiami sulle funzioni derivabili (con introduzione di alcune proprietà di cui vedrete la dimostrazione a "teoria").

Regola dell'Hopital - 1
Se f(x) → 0 e g(x) → 0 per x → c,  f'(c) e g'(c) esistono e g'(c) ≠ 0,  allora f(x)/g(x) → f'(c)/g'(c) per x → c.

Questa "regola" è evidente pensando al fatto che posso approssimare f e g con le funzioni lineari che in c hanno grafico tangente ai loro grafici:
    f(x) = f'(c)(x-c) + o(x-c)
    g(x) = g'(c)(x-c) + o(x-c)
    f(x)/g(x) si comporta come f'(c)(x-c)/(g'(c)(x-c)) = f'(c)/g'(c)
[se i grafici in c intersecano l'asse x, il rapporto tra le funzioni avvicinandosi a c tende a comportarsi come il rapporto delle pendenze]

Quella che è significativa è la
Regola dell'Hopital - 2
Siano f e g derivabili in [a,c) e continue in [a,c]; siano f(x) e g(x) entrambe inf.mi o entrambe inf.ti per x → c.
Allora per x → c  f(x)/g(x) → α  se  f'(x)/g'(x) → α.

Esempi d'uso.

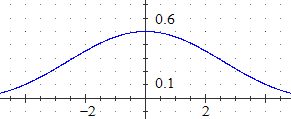
• Come si comporta (1−cos(x))/x2 per x → 0?  È il rapporto tra due infinitesimi (per x → 0).  Provo a studiare il limite del rapporto delle loro derivate: sin(x)/(2x) = sin(x)/x/2 → 1/2 per x → 0. Quindi per la (seconda) Regola dell'Hopital posso concludere che per x → 0 anche (1−cos(x))/x2 → 1/2.   A destra la conferma grafica del limite, che (con Poligon o con una calcolatrice) avremmo potuto avere anche numericamente: definita  F(x) = (1-COS(x))/x^2  avrei ottenuto  F(1)=0.4596976941318602, F(1/10)=0.4995834721974178, F(1/100)=0.4999958333473664, F(1/1000)=0.4999999583255033.

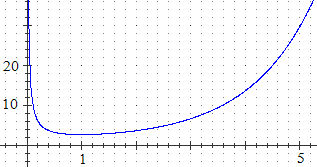
• Come si comporta per x → ∞ il rapporto tra infiniti  ex / x ?   (già visto nel primo link) Vedo se posso ricondurmi al limite del rapporto tra le loro derivate.  ex / 1 = ex → ∞ per x → ∞. Questo (per la seconda regola dell'Hopital) è dunque il limite cercato.   A destra la conferma grafica del limite, che (con Poligon o con una calcolatrice) avremmo potuto avere anche numericamente: definita  G(x) = EXP(x)/x  avrei ottenuto  G(1)=2.718281828459045, G(10)=2202.646579480672, G(100)=2.688117141816136E41.

L'"inverso" non vale

A destra si intuisce dal grafico che il limite per x → 0 di  x2sin(1/x) / sin(x)  sia 0. La cosa è suggerita anche dalle uscite numeriche: posto H(x) = x^2*SIN(1/x)/SIN(x)  ho  H(10^-1)=-0.05449288716762096, H(10^-3)=0.0008268796783452753, H(10^-5)=3.574879798715481E-7, H(10^-7)=4.205477931907715E-8.  Del resto: x2sin(1/x) / sin(x) = x/sin(x) · x · sin(1/x)  è il prodotto di una funzione che tende a 1 per una funzione che tende a 0, prodotto che viene moltiplicato per una che oscilla tra −1 ed 1; quindi, in definitiva, è il prodotto di una funzione che tende a 0, x/sin(x)·x, per una compresa tra due numeri, sin(1/x), e quindi tende a 0.     Invece il rapporto tra le derivate  (2x sin(1/x) − cos(1/x)) / cos(x)  per x → 0 tende a comportarsi come  −cos(1/x)  in quanto 2x sin(1/x) → 0 e cos(x) → 1, e quindi non ha limite:  −cos(1/x) per x → 0 oscilla tra −1 e 1. 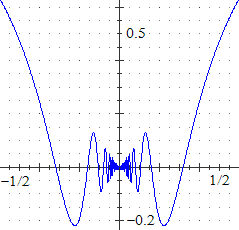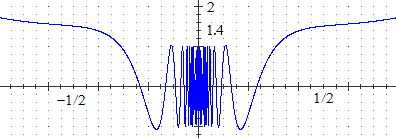Sotto è rappresentato il grafico di x → (2x·sin(1/x)−cos(1/x))/cos(x).

L'Hopital si può applicare ripetutamente, ma a volte l'applicazione allontana dalla meta. Esempio: se studio come si comporta  e−x / (1/x)  per x → ∞ riconducendomi al limite delle derivate ottengo  e−x / (1/x2)  che continua a tendere a "0/0"; se derivo ulteriormente i termini del rapporto ottengo  e−x / (2/x3)  che continua sempre a "0/0": di male in peggio. Invece, con una semplice manipolazione, avrei ottenuto  e−x / (1/x)  =  x / ex → 0  (infatti ex tende all'infinito più velocemente di x). 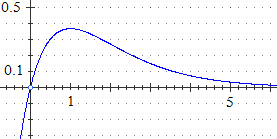Ecco, a destra, che cosa avrei ottenuto rappresentando graficamente la funzione.

− − − − − − − − − − − − − − − − − − −

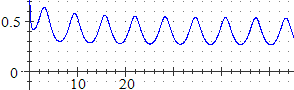
Altri esempi. • (x+√x) / (3x+sin x)  per x → ∞ come si comporta?     Sperimentalmente: f(x) = (x+SQR(x))/(3*x+SIN(x)) f(1) = 0.5206338946485666 f(10) = 0.446845705237596 f(1E2) = 0.367286604389676 f(1E8) = 0.3333666656314087 f(1E12) = 0.3333336666667346 A destra il grafico.     Teoricamente:

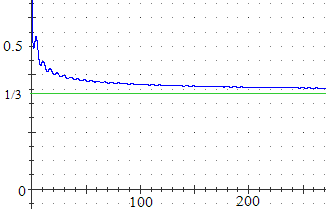(x + o(x)) / (3x + o(x)) → 1/3  (per x → ∞ √x e sin(x) sono trascurabili rispetto ad x)

Con l'Hopital, invece: (1 + 1/(2√x)) / (3 + cos(x)).  È un termine che per x → ∞ tende ad oscillare tra 1/4  (3+1 = 4)  e 1/2  (3−1 = 2)  - a destra un suo grafico - e quindi non converge. Applicando ulteriormente l'Hopital non se ne può quindi uscire (altrimenti anche questo termine dovrebbere avere un limite).

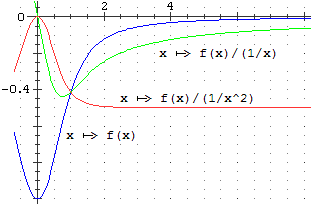
• Qual è l'ordine di inf.mo di x2−√(x4+1) per x → ∞? A destra abbiamo la rappresentazione grafica della nostra funzione, indicata con f, e delle funzioni ottenute dividendo f(x) per 1/x e per 1/x2. Dal comportamento di questi grafici abbiamo subito che f(x) ha, per x → ∞, lo stesso ordine di infinitesimo di 1/x2. Abbiamo che il rapporto di f(x) con tale funzione sembra tendere a 1/2, per cui possiamo dedurre che, presumibilmente, per x → ∞  f(x) = −1/(2x2) + o(1/x2). Potremmo verificare ciò anche con le uscite numeriche di un programma. Ad es. con Poligon abbiamo: F(x) = x^2-SQR(x^4+1) H(x) = -1/(2*x^2)/F(x) H(1) = 1.207106781186547,  H(2^1) = 1.015388203202207,  H(2^3) = 1.000061031432097,  H(2^5) = 1.000000238418636,  H(2^7) = 1   OK     Come avere una conferma "teorica"? Procediamo così: x2−√(x4+1) = (x2−√(x4+1))·(x2+√(x4+1)) / (x2+√(x4+1)) = [usiamo (a-b)(a+b) = a2-b2] (x4−(x4+1)) / (x2+√(x4+1)) = −1 / (x2+√(x4+1)) → 0  come  −1 / (2x2)  (per x → ∞)

• g(x) = tan(x)−x è un infinitesimo per x → 0. Di che ordine?     I grafici (blu e verde) a destra ricordano che sia x che tan(x) per x → 0 sono infinitesimi.  Il fatto che x → x e che x → tan(x) abbiano grafici che tagliano l'asse x con pendenza diversa da 0 fa capire che si tratta di due funzioni infinitesime di ordine 1 (nel caso di x → x era in realtà ovvio).  Il grafico di x → x/tan(x) (nero) passa per il punto (0,1): il fatto che non passi per (0,0) conferma che tan(x) è un infinitesimo dello stesso ordine di x, e il fatto che l'ordinata sia 1 ci fa capire che tan(x) ha x come parte principale.     Dunque  g: x → tan(x) − x  in quanto differenza di due infinitesimi di ordine 1 è un infinitesimo di ordine superiore. Il grafico di g (blu, nella seconda figura) conferma tale ipotesi (il grafico di g tende a spiaccicarsi sull'asse x attorno ad x=0). Il grafico del rapporto  x → g(x)/x2  (è il grafico arancione nella seconda figura) tende a passare per l'origine senza spiaccicarsi sull'asse x: capiamo che tale funzione tende a comportarsi come una retta passante per l'origine senza essere tangente all'asse x, e che quindi si tratti di un infinitesimo di ordine 1.     A conferma di ciò abbiamo che  x → g(x)/x3  ha grafico (verde, nella seconda figura) non passante per l'origine. Dunque g è un infinitesimo di ordine 3. Il grafico del reciproco  x → x3/g(x)  (rosso, nella seconda figura) sembra passare per y=3, e quindi assicurare che g(x) = x3/3 + o(x3).     Alla stessa conclusione possiamo arrivare ragionando numericamente: g(x) = tan(x)-x g(1) = 0.5574077246549023,  g(1E-1) = 0.0003346720854505436,  g(1E-2) = 3.33346667207024E-7,  g(1E-3) = 3.33333466731589E-10 Capisco che tende a 0 come x3 (al dividersi dell'input per 10 l'output tende a dividersi per 103); prendo: h(x) = x^3/(tan(x)-x) e calcolo: h(1E-1) = 2.987999428317352,  h(1E-3) = 2.999998799416179,  h(1E-5) = 3.000004118408791. Capisco che g(x) = tan(x)−x = x3/3 + o(x3).     A questa ricerca "sperimentale" possiamo affiancare la regola dell'Hopital (usiamo D al posto di Dx):

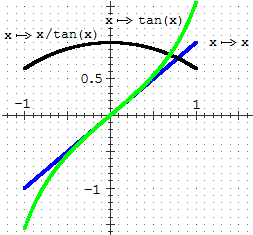
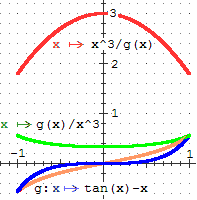
tan(x)-x ———————— —> ? x^3

D(tan(x)-x) 1+tan(x)^2-1 ——————————— = ———————————— —> 1/3 D(x^3) 3*x^2

− − − − − − − − − − − − − − − − − − −

La funzione F: x → x·sin(x), dato che −1 ≤ sin(x) ≤ 1, oscilla tra i grafici di x → x e di x → −x. Trova, a destra dell'origine, il primo punto di tangenza del grafico di F al grafico di x → x e (aiutandoti con Poligon) il primo, a destra dell'origine, punto di massimo di F  [ apri i commenti, seleziona e copia tutto, quindi aziona CLP; usiamo questo demo per dare una spiegazione animata: non dovete imparare i comandi qui usati ].
[ qui trovi alcune delle immagini prodotte dal demo ]

Esercizio 1  e  soluzione (all'es. 12 del link)

Come avrei potuto operare con Poligon (capite i comandi):

N L(x)=2*SQR(x^2+100)-x+24 plot x: 0..24 y:L | 14 oo stop scala sx:-5..40 sy:-10..60 stop [0,24] L MIN

Esercizio 5 del nuovo foglio di esercizi   [e soluzione (all'es. 11 del link)]

Esercizio 2  e  soluzione (all'es. 11 del link) e avvio a nuove problematiche.

Per affrontare i quesiti 15 e 16 dell'ultimo foglio:    sulle curve (cenni: sono argomenti di base, ma forse non li vedrete in alcun corso, e non saranno oggetto di verifica scritta, ma ...)

Alcune prove degli anni passati:
   uno     due     tre 

Soluzioni a "uno":
soluzione all'es. 3 (es 6 del link)
soluzione all'es. 2 (es 12 del link)
soluzione all'es. 1 (es 5 del link)

La volta prossima discuteremo le soluzioni alle altre due prove elencate, anche alla luce di alcuni nuovi argomenti (in particolare in relazione all'individuazione dei punti di "flesso"), e completeremo la soluzione dell'es.1 delle prova "uno".