Commenti agli esercizi

(1) Descrivi sinteticamente le principali differenze epistemologiche (e le connesse specificità didattiche) della matematica rispetto alle altre discipline.

Si vedano le considerazioni svolte nella prima lezione o in uno degli articoli citati (punto 7).

(2) Fai un esempio di modello matematico descrittivo e uno di modello matematico normativo affrontabili nell'insegnamento della matematica ma che abbiano agganci (quali? come sviluppabili?) con altre discipline di insegnamento.

Un modello descrittivo di una situazione, un fenomeno, … è una rappresentazione mediante oggetti matematici del suo aspetto, comportamento, …: ad esempio la descrizione di come una grandezza fisica B varia in funzione di un'altra grandezza A mediante la rappresentazione sul piano cartesiano delle coppie di dati sperimentali cosituite ciascuna da una misura di A e dalla corrispondente misura di B; oppure la descrizione delle caratteristiche fisiche di una popolazione medainte la altezza media, il peso medio, ….
    Un modello normativo è la regolazione mediante oggetti matematici dell'evoluzione di un fenomeno, del comportamento di un macchinario, …: ad esempio i modelli matematici incoportati sotto forma di software nei più disparati dispositivi, le formule con cui vengono determinati i punteggi in un concorso, ….
    Ci sono intrecci tra i due aspetti. Ad esempio se analizzassi dei dati relativi all'allungamento di un oggetto al variare delle temperatura scoprirei che un modello descrittivo adatto al fenomeno è la proporzionalità tra le variazioni di temperatura e quelle di lunghezza; ma una riflessione più approfondita mi consente di scoprire il modello matematico normativo che è incorporato nella definizione (classica) di temperatura: io fisso in 0° e 100° i valori di due particolari stati termici (acqua fondente e acqua in ebollizione) e poi definisco la temeperatura assumendo che le sue variazioni siano proporzionali alle variazioni della lunghezza della colonnina (ossia supponendo che le divisioni uguali che traccio sul termometro corrispondano tutte a una stessa variazione di temperatura).
    Considerazioni su questi aspetti (ed esempi di possibili attività didattiche) si trovano in alcuni articoli a cui si è fatto riferimento: ad es. qui (punto 13),  qui (punti 2-4)  o qui (punto 2.3).

(3) Quali tipi di difficoltà mediamente può trovare uno studente di fine superiori (in Italia ai nostri giorni) di fronte alla risoluzione di una disequazione come x² > 1/4 e che cosa ne potrebbe essere all'origine?

Di fronte a x² > 1/4 ci si aspetta che molti studenti rispondano x > ±1/2, per analogia con la risoluzione di x² = 1/4. Ci si aspetta anche che, tra coloro che capiscono quale sia la soluzione, molti la esprimano in modo errato, ad esempio con "x < -1/2 e x > 1/2" invece che con "x < -1/2 o x > 1/2".
Anche tra coloro che rispondono correttamente, ci aspettiamo che non pochi usino formule e tecniche di manipolazione generali per risolvere disequazioni del tipo ax^2+bx+c > 0 invece che ragionare direttamente su questo, semplice, caso particolare.
All'origine di queste difficoltà vi è la tendenza, da parte degli alunni, ad applicare procedimenti risolutivi appresi solo meccanicamente: perso l'allenamento a risolvere esercizi di un certo tipo, non riescono a ricordarne i corripondenti metodi risolutivi o non sono più in grado di associare procedimenti a problemi corrispondenti. Questa tendenza è favorita da un insegnamento che articola la matematica in tanti temi e attività separate, e che in particolare non mette a fuoco le poche idee generali che servono per risolvere tutti i tipi di disequazioni (assieme alle caratteristiche delle particolari funzioni via via coinvolte) e che non intreccia metodi simbolici e metodi grafici (idee generali e intreccio che, a differenza delle singole procedure risolutive, gli alunni avrebbero occasione di rivedere, consolidare, applicare, … nel corso di tutto il quinquennio).
    La presenza di difficoltà di questo tipo sono state evidenziate dall'indagine sulle competenze degli alunni dell'ultimo anno delle superiori discussa nel corso di Laboratorio: l'indagine, la domanda sulle disequazioni, i commenti ad essa (clicca su >>>).

(4) La composizione delle variazioni relative è commutativa? Proponi un esercizio a risposta chiusa (con aggiunta una opportuna domanda di controllo per verificare se l'eventuale risposta corretta è stata casuale) per verificare la comprensione di questo fatto (la commutatività o la non commutatività, a seconda di come hai risposto alla domanda precedente).

Un esempio (a 5 alternative) potrebbe essere il terzo esercizio riportato qui (es. 3.3 sui Rapporti dagli OM), che mira a una verifica della padronanza operativa in un contesto economico della proprietà; una verifica più interna avrebbe potuto limitarsi a confrontare gli ordini con cui comporre due variazioni percentuali.  Altri esercizi possono essere suggeriti dagli altri esempi riportati nella stessa pagina o in pagine seguenti dell'eserciziario a cui siete stati colleagti.  La domanda di controllo può andare da un semplice "perché?", che coinvolge, però anche conoscenze e competenze di tipo diverso da quelle della padronanza operativa della proprietà, a, per es., "e se sconto e tassa fossero state del 10% avresti dato la stessa risposta?"

(5) Come spiegheresti in modo didatticamente efficace (a un alunno del triennio) la risoluzione rispetto a x e quella rispetto a k (x e k a valori reali) della disequazione k/x > x?

• Risoluz. di k/x > x rispetto a x.
Devi trovare per quali valori di x k/x è maggiore di x. Prima di metterti a fare calcoli ti conviene interpretare graficamente il problema: devi trovare, al variare del parametro k, per quali ascisse la curva y=k/x sta sopra alla curva y=x. Tieni in ogni caso conto che per x=0 la disequazione non è definita.
– Per k>0 si tratta di iperboli collocate nel 1° e 3° quadrante, di alcune delle quali sotto è schizzato l'andamento. Si tratta di curve simmetriche rispetto agli assi e alla retta y=x. y=k/x interseca y=x quando k/x=x, ossia quando x=√k e quando x=-√k. Tenendo conto dei grafici, possiamo concludere che la disequazione equivale a 0 < x < √k OR x > -√k, ovvero che le soluzioni formano l'insieme (-∞,-√k) U (0,√k)
– Per k<0 si tratta di iperboli collocate nel 2° e 4° quadrante. I rami nel 2° quadrante stanno sopra a y=x, gli altri sotto. Possiamo concludere che la disequazione equivale a x <0, ovvero che le soluzioni formano l'insieme (-∞,0)
– Per k=0 si tratta dell'asse x, esclusa l'origine, in quanto y=0/x per x=0 non è definito. L'asse x sta sopra a y=x per x < 0. Le soluzioni formano l'insieme (-∞,0).

Potevi procedere anche senza riferirti ai grafici:
– per x = 0 la disequazione non è definita;
– cerchiamo le soluzioni positive; se x>0 posso moltiplicare per x entrambi i termini senza modificare il segno di disegualianza; mi riconduco a x²< k e, quindi, se k > 0, a 0 < x < √k; se k ≤ 0 non vi sono soluzioni positive.
– cerchiamo le soluzioni negative; se x<0 posso moltiplicare per x entrambi i termini modificando il segno di disegualianza; mi riconduco a x²> k e, quindi, se k ≤ 0 ogni x (x < 0) è soluzione; se k > 0 occorre che il valore assoluto di x (-x) sia maggiore di √k, ossia x < √k (ovvero la parabola y = x² sta sotto a y=k per x < √k).
In definitiva, se k < 0 ...; se ...
• Risoluz. di k/x > x rispetto a k.
Se vuoi interpretare la disequazione graficamente, ti può essere psicologicamente comodo indicare con x l'incognita e con una lettera diversa da x il parametro, ad esempio usare q al posto di x e x al posto di k, ossia pensare alla risoluz. di x/q > q rispetto a x.
– se q>0 y=x/q è una retta con pendenza positiva; essa sta sopra a y=q a destra del punto di intersezione. Questo ha x tale che x/q=q, ossia x=q². Le soluzioni formano dunque l'intervallo (q²,∞). In altre parole per x>0 la disequazione originale equivale a k>q²
– se q<0 y=x/q è una retta con pendenza negativa; essa sta sopra a y=q a sinsitra del punto di intersezione. Le soluzioni formano dunque l'intervallo (-∞,q²). In altre parole per x<0 la disequazione originale equivale a k<q².
– se q=0, ossia se x=0, la disequazione non è definita.
Potevi procedere anche senza riferirti ai grafici. In questo caso è più facile che nel caso precedente, in quanto il modo in cui trasformare l'equazione dipende dal segno del parametro, non da quello dell'incognita:
…
    Riferimenti qui ("risoluz.equaz.2", e commenti nei punti precedenti)

(6) Verifica sperimentalmente il "teorema di Pitagora" nel caso sotto illustrato.
In quale o quali contesti didattici potrebbe aver senso una tale "verifica", e una riflessione su di essa?

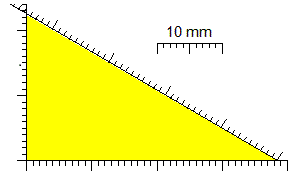
Supponiamo che il triangolo sia esattamente rettangolare. Un cateto è lungo tra 22 e 23 mm; l'altro è lungo tra 38 e 39 mm; l'ipotenusa è lunga tra 44 e 45 mm.
La somma dei quadrati dei cateti (espressa in mm²) cade tra 22^2+38^2 = 1928 e 23^2+39^2 = 2050. Il quadrato dell'ipotenusa cade tra 44^2 = 1936 e 45^2 = 2025.
Gli intervalli [1928, 2050] e [1936, 2025] hanno intersezione non vuota (hanno l'intervallo [1936, 2025] in comune). Quindi il nostro rilevamento è in accordo col teorema di Pitagora.

Si tratta di una attività di calcolo approssimato che potrebbe essere svolta in vari contesti didattici. Ad esempio nell'ambito di una attivtà di avvio al laboratorio di fisica, effettuabile in classe. O nell'ambito di una riflessione più generale sul significato della verifica sperimentale di una legge fisica o di una formula riferita ad altri ambiti disciplinari, o sull'uso del simbolo "=" per indicare valori arrotondati: si tratta di casi in cui le eguaglianze devono essere intese in senso approssimato ( calcolo approssimato neGli Oggetti Matematici). Oppure potrebbe essere spunto per una riflessione sulla natura dei modelli matematci e, in particolare, della definizione matematica di spazio ( distanza e triangoli neGli Oggetti Matematici: si tratta di considerazioni riferite all'approccio alla geometria scelto negli Oggetti Matematici, ma che possono essere applicate ad altri approcci, anche ad uno assiomatico-tradizionale, nel momento in cui si vuole fare una riflessione sulla natura della matematica o, in particolare, sulla possibilità di altre "geometrie", o sulla storia della geometria - si vedano le considerazioni storiche svolte a lezione).

(7) Il poliedro sotto rappresentato da più punti di vista rappresenta il dominio dei vincoli di un problema di massimizzazione di una funzione obiettivo lineare F a tre input la cui soluzione con il metodo del simplesso dà luogo alla sequenza di vertici: O-A-B-C. Quale tra i seguenti termini è F(x,y,z)?
(a) 4x+2y+z (b) 3x+y+2z (c) x+y+2z

I vertici che hanno lati in comune con O sono A=(3,0,0), D=(0,0,3) e E=(0,3,0). Indichiamo con Fa, Fb, Fc la funzione che a (x,y,z) associa rispettivamente (a), (b), (c). Fa(O)=Fb(O)=Fc(O)=0.
    Consideriamo Fa. Fa(A)=12, Fa(D)=3, Fa(E)=6. Quindi il se F fosse Fa il primo tratto del percorso sarebbe O-A.
I vertici che hanno lati in comune con A sono, oltre a O, B=(2,0,3) e G=(3,2,0). Fa(B)=11, Fa(G)=16. Quindi il percorso inzierebbe con O-A-G, non con O-A-B. F non può essere Fa.
    Consideriamo Fb. Fb(A)=9, Fb(D)=6, Fb(E)=3. Il primo tratto sarebbe O-A.
Fb(B)=12, Fb(G)=11. Il vertice successivo sarebbe B. Verifichiamo se il vertice successivo sarebbe C.
I vertici che hanno lati in comune con B sono A e D, già considerati, e C. Fb(C)=13, che è maggiore di Fb(B). Il percorso inizierebbe con O-A-B-C. Verifichiamo che finisce con C.
I vertici che hanno lati in comune con C sono B e G, già considerati, e H=(1,2,3). Fb(H)=11, che è minore di 13. Quindi il percorso è O-A-B-C.
    Dato che la risposta giusta è una sola potremmo fermarci qui. Per individuare eventuali errori possiamo controllare che cosa accade anche per (c).
Fc(A)=3, Fc(D)=6, Fc(E)=3. Quindi il primo tratto sarebbe O-D.
  Concludendo F=Fb.
    Vedi appunti di Canepa.

(8) Costruire il modello matematico del problema:
Un commerciante, che ha una capacità di magazzino di 1500 kg, può acquistare una merce a 60 euro al kg se la quantità è al più 100 kg; se la quantità acquistata supera 100 kg usufruisce di uno sconto del 30% sull'eccedenza. Tenendo conto del fatto che all’atto dell’acquisto egli deve sostenere un costo fisso di 1000 euro, e che il prezzo unitario in euro di rivendita della merce è dato da p = 90 - x/50 (con x = quantità in kg), determinare quale quantità deve essere acquistata e venduta (a un unico cliente) per ottenere il massimo guadagno.

Stiamo supponendo che il commerciante riesca a vendere (a un solo cliente) tutta la merce che acquista e che i costi sostenuti siano solo quelli per l'acquisto della merce e un costo fisso di 1000 €.
Sia C(x) il costo per l'acquisto di x kg. C(x) = 60x se x≤100, c(x) = 60·100 + 0.7·60(x-100) altrimenti.
Il prezzo di vendita di 1 kg è p(x) = 90 - x/50 (a chi compra più merce viene praticato un prezzo inferiore).
Sia G(x) il guadagno totale corrispondente all'acquisto (e vendita) di x kg di merce. Il problema consiste nel trovare per quale x G(x) è massimo. Dobbiamo esprimere matematicamente G(x).
G(x) = p(x)·x - C(x) - 1000.

G(x) =	{	–x2/50 + 30x - 1000   se 0 ≤ x ≤ 100
		–x2/50 + 48x - 2800   se 100 < x ≤ 1500

Non era richiesta la soluzione. Comunque ecco la soluzione usando Poligon:
G(x)=(x<100)*(-x^2/50+30*x-1000)+(x>=100)*(-x^2/50+48*x-2800) plot x:0..1500 y:G [0, 1500] G max   se x = 1200  y = 26000

    Vedi appunti di Canepa.

(9) Sotto sono riprodotte, "incollate" su carta millimetrata, una figura, a sinistra, realizzata con Paint e l'esito di due sue successive trasformazioni, realizzate sempre con Paint.
(1) Quali comandi (e con quali parametri) sono stati utilizzati?
(2) Queste trasformazioni potrebbero essere realizzate con due successive proiezioni da un piano ad un altro. Specifica per ciascuna se si tratta di una proiezione centrale o parallela, e come sono collocati piano di partenza, piano d'arrivo e raggi proiettanti.
(3) L'esercizio ti suggerisce (direttamente o indirettamente) qualche considerazione didattica sui collegamenti tra l'insegnamento della geometria piana e quello della geometria tridimensionale.
 

(1) Prima un "ridimensionamento" poi un "inclinamento", con i parametri riprodotti nella figura a lato. (2a) La prima trasformazione (una riduzione di scala monometrica, con fattore di scala 1/2), è realizzabile proiettando centralmente la figura con piano di arrivo parallelo al piano di partenza ed equidistante da questo e dal centro di proiezione (vedi figura (I) sotto a sinistra; nel caso (J) la riduzione di scala verrebbe composta con una rotazione di 180°; si otterrebbe la stessa figura, a meno di una isometria).
(2b) La seconda trasformazione è realizzabile mediante una opportuna proiezione parallela da un piano su un altro piano opportunamente inclinato. Per capire meglio la disposizione complessiva può essere utile provare a trasformare nello stesso modo una figura più articolata, come la seguente, e pensarla come ombra della figura originale disegnata su un vetro. Ci si convince facilmene che la si può ottenere, ad esempio, se la luce arriva come illustrato nella figura qui a destra. Non sarebbe facile descrivere questa disposizione a parole (senza ricorrere al sistema di riferimento xyz [lato a sull'asse x, piano di partenza: y=0, piano di arrivo: z=0, direzione proiezione: vettore (1,1,-1)] e/o a un sistema di riferimento polare). Proviamo (ma, certamente, non si tratterà di una descrizione agevolmente comprensibile):  il piano di arrivo è perpendicolare al piano di partenza e lo interseca in una retta parallela al lato a della figura originale; la proiezione ha direzione parallela ai piani perpendicolari al piano di arrivo e inclinati di 45° rispetto al piano di partenza e ai piani inclinati di 45° rispetto sia al piano di arrivo che a quello di partenza.
Per approfondimenti cerca, nell'indice alfabetico degli Oggetti Matematici, le voci "inclinamento" e "proiezione".
(3) • l'importanza di affrontare anche lo studio della geometria tridimensionale, impostato, come nel caso piano, non limitandosi allo studio di "figure" ma affrontando lo sudio dello "spazio" (sistemi di riferimento, coordinate, direzioni, ...), • l'opportunità di affrontare, intreccandosi anche ad altre discipline (scienze-geografia, arte/disegno-prospettiva, fisica-ottica), • la problematica della rappresentazione piana di figure tridimensionali, • la motivazione dello studio delle trasformazioni geometriche piane (e delle coniche) attraverso la loro interpretazione 3D, • la modellizzazione di problemi spaziali e la loro riconduzione a problemi di geometria piana (si pensi ai quesiti sulle ombre o sulla "formichina" discussi a lezione, e ai relativi commenti), ...

(10) Il cerchio a alto, rappresentato nel piano complesso, viene trasformato mediante la funzione F: C-{0} → C tale che F(z) = 1/z. Quale, tra le seguenti, è la sua immagine mediante F? Quale strategia hai usato per risolvere il problema?     (A) α   (B) β   (C) γ   (D) δ   (E) ε