Matematica ed Arte

Stage per gli studenti della scuola secondaria - Carlo Dapueto

http://macosa.dima.unige.it/stage/2024.htm

Accompagneremo la discussione con delle attività di laboratorio in cui faremo qualche esempio di impiego di WolframAlpha, il software matematico più diffuso al mondo, impiegabile in tutti i livelli scolastici, dalla scuola di base all'università, per il quale esiste una versione online usabile liberamente.  Faremo anche impiego di altro software online.  Inquadreremo tutto in una conversazione più generale sui rapporti tra matematica ed arte.

|01|  La matematica non ha un contesto particolare di riferimento.  Le altre discipline scientifiche (a parte l'informatica e altri settori di ricerca "figli" della matematica) hanno invece dei particolari ambiti di applicazione, e tutte si servono della matematica per costruire i loro modelli e, a volte, sollecitano la costruzione o l'invenzione di nuovi concetti e nuovi strumenti matematici.
    Questo (l'avvalersi della matematica) vale non solo per le discipline scientifiche ma anche per molte altre discipline (e tecniche), e in particolare per l'arte.

|02|  Nel medioevo, grammatica, retorica, matematica, musica e astronomia venivano indicate come arti liberali, contrapposte alle arti meccaniche, dal carattere più tecnico che intellettuale, e fra queste erano comprese le arti figurative.  Progressivamente si arrivò, col Rinascimento, al concetto moderno di arte come attività umana volta a creare un'opera di bellezza, distinta dalla tecnica.  Si è venuta così formando la concezione moderna di arte,  che non è più praticata solo a servizio della Chiesa o della nobiltà, ma è da apprezzare in quanto tale,  e che comprende, oltre alle arti figurative (pittura, scultura, architettura), le arti minori (ceramica, vetraria, oreficeria, ...), l'arte musicale, l'arte fotografica, l'arte cinematografica, ...
    Qui parleremo solo dell'arte musicale e delle arti figurative. Partiamo da queste ultime.

 

|03|  Le prime manifestazioni artistiche, legate alla caccia, risalgono alla fine del paleolitico, decine di millenni avanti Cristo.  Nel neolitico (~ 10000-3000 a.C.), con la nascita della pastorizia e della coltivazione, le immagini si fanno più statiche, compaiono i primi segni geometrici:  i bisonti vengono disegnati tutti "eguali", sui vasi di terracotta vengono tracciati segni colorati come ornamenti, si sviluppa il culto dei morti e sulle costruzioni votate ad esso vengono collocate suppellettili che non hanno funzioni d'uso, vengono realizzate le prime costruzioni "stabili", come i nuraghi.  Poi si formano i grandi stati monarchici, la cui cultura artistica avrà una forte influenza sul formarsi della civiltà artistica mediterranea.  Si arriva al periodo classico dell'arte greca (IV sec. a.C.), in cui (sia nell'architettura che nella scultura e nella pittura) l'armonia, il rapporto tra le parti e il tutto si esprime attraverso leggi formali.  La matematica interviene nella definizione di alcuni rapporti tra le dimensioni delle varie parti del corpo umano o, per esempio, tra i diametri di una colonna alle varie altezze di essa.
    Interviene, ovviamente, anche nella costruzione degli edifici. Sotto la forma ellittica del Colosseo.

Colosseo:

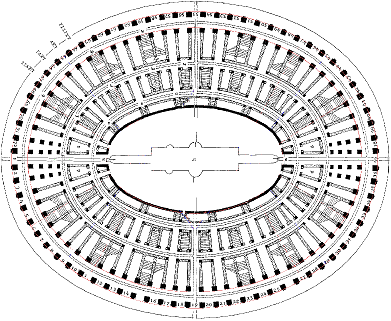
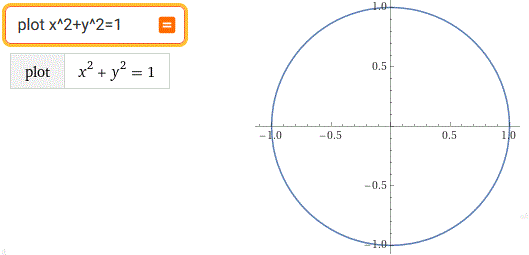
|04|  Proviamo a tracciare la visione dall'alto del Colosseo, e in particolare le due ellissi che delimitano le gradinate e la pista interna.  Le ellissi cosa sono:  sono dei cerchi schiacciati che si ottengono facilmente dalla equazione del cerchio.  Procediamo usando WolframAlpha.  Prima vediamo come si traccia un cerchio.  Clicca:

WolframAlpha

Scrivi (o copia e incolla)     plot x^2+y^2 = 1

Per ottenere un'ellisse (che non sia un cerchio) basta che schiacciamo questa figura in una qualche direzione. Vediamo che cosa otteniamo con l'equazione    plot x^2 + (2*y)^2 = 1

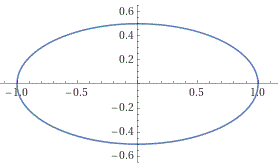
Le intersezioni con l'asse y sono -0.5 e 0.5, infatti per x=0  (l'asse y)  l'equazione diventa  (2*y)^2 = 1,  ossia  2*y = 1 OR 2*y = -1,  ossia  y = 1/2 OR y = -1/2.
In pratica, per moltiplicare per 1/2 le y ho messo 2*y al posto di y.

Ecco, sotto, l'immagine del Colosseo con indicate le lunghezze in pixel dei cosiddetti "asse maggiore" e "asse minore" delle due ellissi, lette direttamente col software per disegnare (Paint o simili), dopo avervi incollato l'immagine (si potrebbero ottenere valori diversi da questi, ma ad essi proporzionali).

 

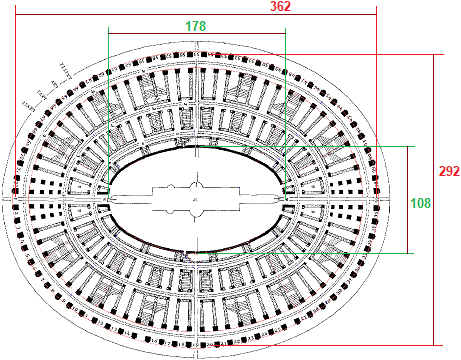
Che cosa sono i pixel? Sono i quadretti la cui unione forma un'immagine sullo schermo di un computer o su una fotografia.

Ecco come posso tracciare il Colosseo con WolframAlpha (copia e incolla la riga scritta in blu):

plot  (x/(362/2))^2+(y/(292/2))^2=1,  (x/(178/2))^2+(y/(108/2))^2=1,  x*y=0

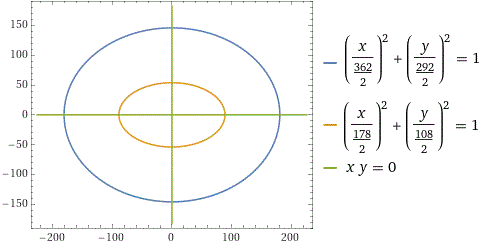
Perché ho scritto, in questo modo, queste equazioni?     ...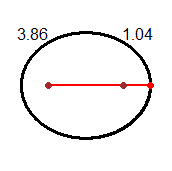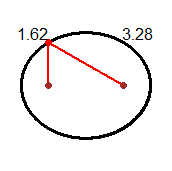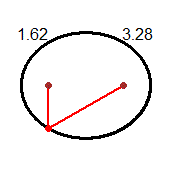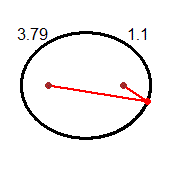
Le ellissi possono essere descritte anche diversamente. Vedi QUI.

Non chiudiamo WolframAlpha: lo useremo ancora.

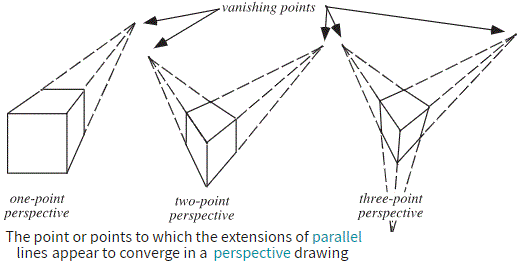
|05|  Come abbiamo accennato nel paragrafo 2, il passaggio delle arti figurative da arti meccaniche ad arti liberali avvenne intorno al XIV secolo.  Un ruolo decisivo lo assunse lo sviluppo delle rappresentazioni prospettiche e il conseguente passaggio degli artisti da "maestri" a "professori".  E, invero, anche a "professori di matematica", come vedremo.

I primi disegni prospettici che  (oggi)  si possono affrontare nei primi anni di scuola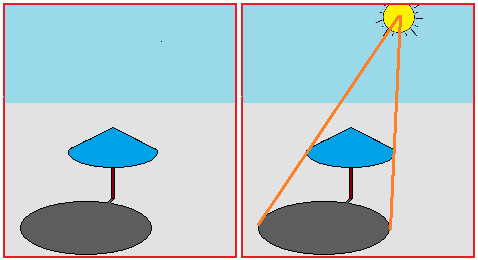

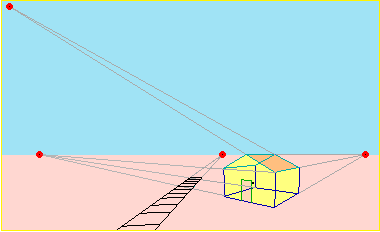Alcuni punti di fuga (pianura, orizzonte, cielo, binario, casa) in un disegno più complesso.

La stessa casetta vista da un elicottero che vola attorno ad essa e poi atterra.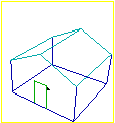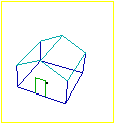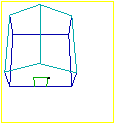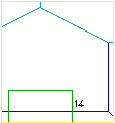

|06|  Qualche (timida) anticipazione:

L'ultima cena (Duccio di Boninsegna, 1310 circa)

Gli elementi del cassettone al centro del soffitto hanno un unico punto di fuga. Gli elementi degli altri cassettoni convergono sull'asse di simmetria. Altri elementi del dipinto (come le strisce sulla tovaglia, che sono perpendicolari al quadro come gli elementi del cassettone) non convergono.

Poi:

San Sebastiano (Antonello da Messina, 1476)

Il punto di vista viene scelto drammaticamente basso.  L'occhio è posto a circa 5 m da S. Sebastiano  (ovvero dal modello che lo rappresenta)  e a circa 30 cm da terra  (ovvero dal piano in cui sta in piedi il modello).

|07|  Come faccio a raggiungere queste conclusioni?  Qual è la matematica che sta dietro alle rappresentazioni prospettiche?  Consideriamo un caso semplice: la rappresentazione delle piastrelle (o delle rette parallele nel piano orizzontale).

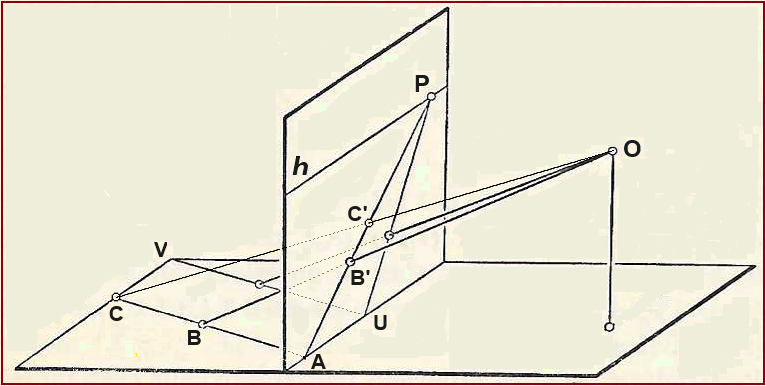
Guardo dal punto di vista O due segmenti uguali e paralleli AC e UV tracciati su un piano orizzontale.  Su un vetro verticale passante per AU vedo i segmenti non più paralleli; se prolungassi i segmenti sul vetro li vedrei confluire in un punto P.  Se tracciassi altri due segmenti paralleli a partire da A e U li vedrei confluire sul vetro in un altro punto della retta orizzontale h che passa per P.  Se prendo B tra A e C sul vetro vedo B' e C' con B'C'/AB' maggiore di BC/AB.  La retta h è costituita dai punti "all'infinito" corrispondenti alle varie direzioni (diverse da AU) sul piano orizzontale.

Dopo alcune anticipazioni di Brunelleschi e Leon Battista Alberti, fu Piero della Francesca a fare una trattazione rigorosa della prospettiva, con il De prospectiva pingendi (~1474).  Le sue spiegazioni non hanno come soggetti esempi pittorici, ma sono argomentazioni e descrizioni di procedimenti di costruzione geometrica generali, che chiama "teoremi".  La figura precedente è simile alle molte presenti nel suo trattato.  Possiamo dire che questo "artista" ha scritto la prima opera sulla branca della matematica che si chiama geometria proiettiva.

In WolframAlpha: artworks of Piero della Francesca La flagellazione, 1460

Oggi, analizzando le foto, per noi è facile capire la prospettiva. Esaminiamo una foto del Loggiato Maggiore del Palazzo Ducale di Genova.    Rette parallele tra loro vengono viste confluire in uno stesso punto:  la balaustra e la sua ombra convergono verso il punto D,  le rette che congiungono la base inferiore del blocco su cui poggia una colonna con la base superiore di quello successivo convergono verso il punto E,  le ombre di pilastrini e colonne convergono vero il punto A,  il lato del porticato perpendicolare a quello visto in primo piano e la linea perpendicolare alla balaustra che separa due tipi di pavimentazione convergono verso B, …    Le rette che stanno su piani orizzontali (ombre di colonne, balaustre, profili del tetto, …) convergono tutti sulla stessa retta, AD.    Le rette che stanno sul piano delle colonne o su piani ad esso paralleli (come il lato opposto del porticato) convergono sulla stessa retta, DF.    Il punto G è quello in cui convergono le rette che congiungono gli elementi reali con le loro ombre: è la posizione del sole.  I raggi del sole arrivano sulla terra praticamente paralleli, quindi G è pensabile anche come il punto di fuga di segmenti paralleli diretti come i raggi del sole.

|08|  Esempi di rappresentazioni prospettiche con WolframAlpha (metti nel box di input i comandi seguenti).

vanishing point

cube

cube view from (3, 1, 1)             center (0,0,0), edge length 1, edges parallel to the axes

cube view from (3, 1, -1)

cube view from (2, 2, 2)

cube view from (1000, 1000, 1000)

cube view from (0, 0, 0)

cuboid 4,3,5 view from (4, 2, 7)

pyramid 3 view from (4, 2, 3)

pyramid 4 view from (4, 2, 3)

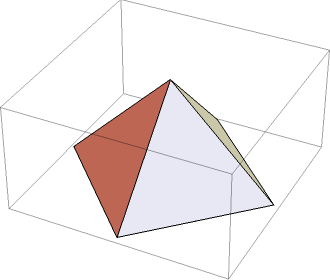
pyramid 4 view from (0, 0, 1000)

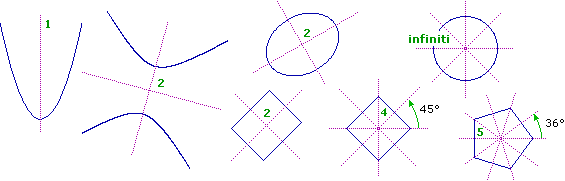
|09|  Un aspetto importante da considerare a scuola sono anche le semplici trasformazioni geometriche piane che intervengono nell'arte, dalle trasformazioni di scala alle simmetrie.  Qualche esempio di figure astratte (con rappresentati gli assi di simmetria) che richiamano, facilmente, opere artistiche che presentano analoghe simmetrie.

Iperboli (due assi e un centro di simmetria):   Camberra, Australia, Parlamento  e  Brasilia, Cattedrale

Sotto un mausoleo tipico dell'architettura moghul (Taj Mahal, ~ 1600).

Le simmetrie con WolframAlpha:

reflect across y=2x    ||    reflect across y=2+x    ||    vertical shear 20 degrees

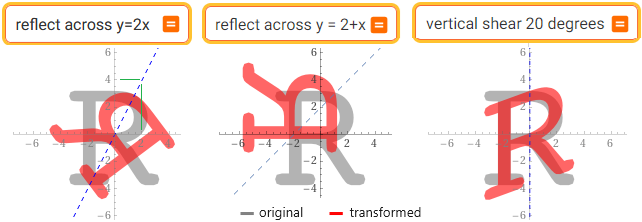
La terza trasformazione non è una simmetria ma una deformazione lineare (in inglese "shearing" che significa "tosatura"). Un altro esempio:

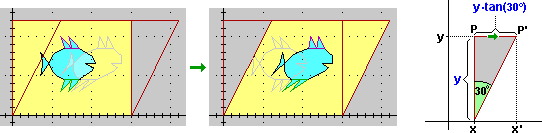
Le simmetrie (sia assiali che centrali) sono poi diventate anche dei concetti per descrivere i grafici delle funzioni.  3 esempi (metti in WolframAlpha la riga seguente):

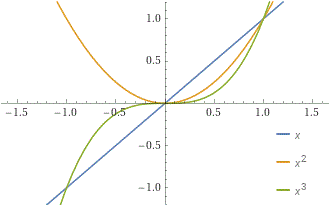
plot  y = x,  y = x^2,  y = x^3,   x = -1.6..1.6,   y = -1.2..1.2

... oltre che la forma di alcune epressioni, la struttura di vari tipi di molecole, la disposizione degli intervalli che rappresentano le soluzioni di particolari disequazioni, …

solve x^2-1 > 0

|10|  Altre figure che, poi, sono state descritte con formule matematiche (l'ultima curva è la forma della conchiglia del nautilo). Metti in WolframAlpha:

quadrifolium, fish curve, cardioid, astroid, golden spiral

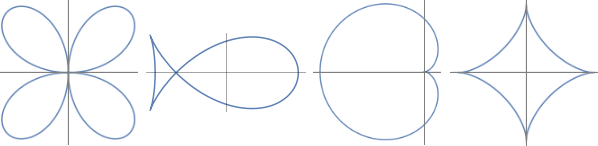
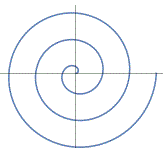
|11|  Un altro aspetto degli intrecci tra matematica ed arte: i paradossi della visione.

Esempi di figure impossibili   (apri con WolframAlpha):
            Penrose triangle                           Penrose stairway

		Varie figure impossibili sono state realizzate dall'artista olandese Maurits Cornelis Escher (1898-1972). A sinistra la litografia "Cascata" che rappresenta un moto perpetuo.  L'abilità dell'artista riesce ad ingannare i nostri sensi, facendoci vedere qualcosa che nella realtà non esiste: l'acqua, prima o poi, deve risalire per poter cadere una seconda volta, e per farla risalire ci vuole almeno la stessa energia che si può ricavare dal mulino;  non è possibile aggirare il principio di conservazione dell'energia.
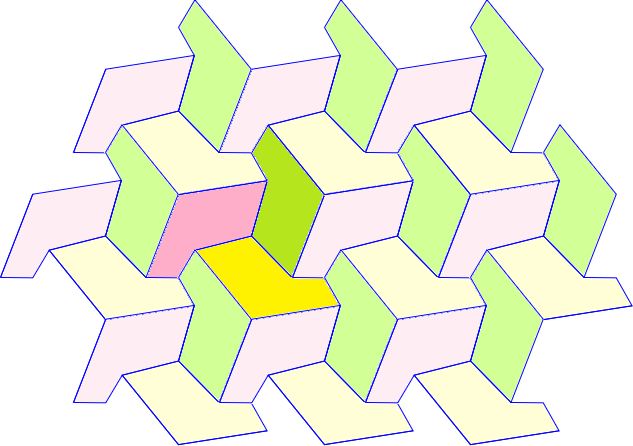
		Escher è famoso anche per la realizzazione di tassellazioni (chiamate anche pavimentazioni) realizzate con figure che non sono dei poligoni regolari, come la seguente.

Una tassellazione è la copertura di una superficie (piana o no) utilizzando una o più forme geometriche senza sovrapposizioni e senza spazi vuoti.  Due esempi classici:

Un mosaico dell'antica Roma e uno islamico a Marrakech

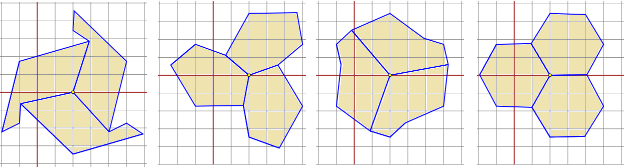
Non è facile capire come costruire tassellazioni che non siano realizzate con poligoni regolari.  Qualche esempio:

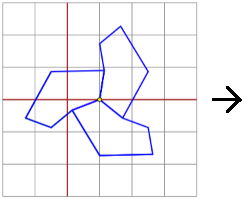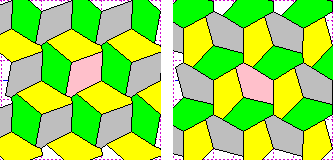Vediamo l'illustrazione della cosa con  questa animazione  (clicca più volte "riavvia").

Ci siamo limitati ad alcuni esagoni non regolari che consentono di tassellare il piano.  Alla fine di questo documento daremo indicazioni di dove sono reperibili condizioni generali per poter realizzare le pavimentazioni, condizioni che sono descritte nell'enuciato noto come teorema di Escher.

|12|  Anche l'arte musicale ha fortissimi intrecci con la matematica. Ne esploreremo, brevemente, alcuni.

Incominciamo a veder rapidamente qualche esempio con WolframAplha (le note sono indicate con le lettere dell'alfabeto, nella notazione originale, di origine greca, usata tuttora nei paesi di lingua inglese e in gran parte degli altri paesi - in Italia si usano do, re, mi, ...); incolliamo le scritte "notes ..." e, poi, clicchiamo "Play Sound".

notes C D E F G A B C B A G F E D C           Scala musicale standard (e ritorno)

notes F# G G A G C B G G A G D C               Tanti auguri a te

notes E D# E D# E B D C A                   Beethoven (Per Elisa)
ovvero:   E4 | D♯4 | E4 | D♯4 | E4 | B3 | D4 | C4 | A3

notes C C# D D# E F F# G G# A A# B C         Scala musicale con tasti bianchi e neri (la frequenza via via raddoppia)
(invece di D#, F#,... si usano anhe Eb, Gb, ...)

 

notes C Eb G C D F A C Fb E
C_4 | Eb_4 | G_4 | C_5 | D_5 | F_5 | A_5 | C_6 | Fb_6 | E_6

Vedremo, poi, alcuni software che consentono di suonare brani interi. Vediamo, ora, altri aspetti.

Osserviamo che in WolframAlpha possiamo approfondire il tema della musica digitando   music   e poi approfondire cliccando   Music Theory.   Accennimo ora qualche altro aspetto matematico.

Le note sono dei piccoli suoni dalle oscillazioni regolari. Consideriamo uno strumento musicale molto semplice, costituito da una lamella metallica fissata per un'estremità a un supporto (figura sotto a sinistra). Se spostiamo e rilasciamo l'estremità libera della lamella, questa si mette a oscillare con frequenza presso che costante, producendo un suono che, trasformato in segnale elettrico, è rappresentabile graficamente come segue:

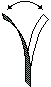
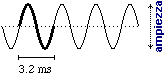
L'ampiezza dell'oscillazione dipende l'intensità dell'effetto sonoro: maggiore è l'ampiezza, maggiore è il volume del suono.  Il grafico di un suono più complesso (un si bemolle da 466 Hz) emesso da un flauto:

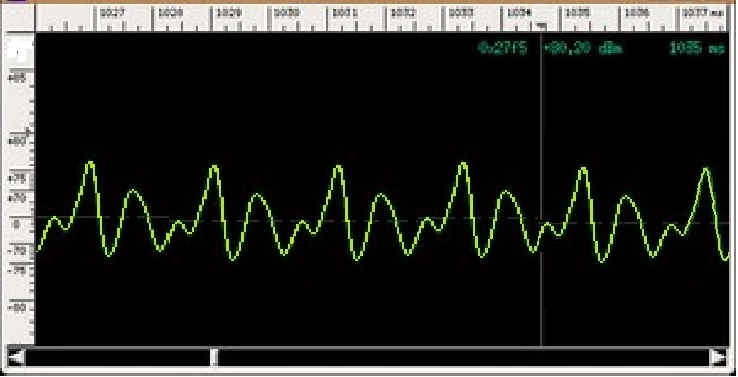
Il grafico del suono prodotto dalla lamella sembra periodico. Ma, in realtà, l'ampiezza delle oscillazioni della lamella man mano diminuisce, anche se lentamente: il grafico pian piano verrebbe deformato mediante una progressiva riduzione della variazione verticale.  Lo stesso si può dire per il suono prodotto da una chitarra o da un tamburo.  La cosa è simile anche per il flauto, anche se invece delle oscillazioni di una lamella o una corda o una membrana abbiamo delle vibrazioni dell'aria.  Ecco un possibile grafico del suono prodotto dalla lamella; introduci in WolframAlpha e osserva quanto ottieni:

Solo con strumenti elettronici, in cui le onde sonore sono prodotte da dispositivi alimentati elettricamente, si possono produrre anche note non smorzate.

Nelle sirene meccaniche le onde sonore sono prodotte soffiando aria contro un disco ruotante dotato di fori. Aumentando la velocità di rotazione viene prodotta un'onda sonora che oscilla sempre più velocemente, ossia un suono man mano più acuto. Questo suono non è, quindi, una "nota". Un esempio:

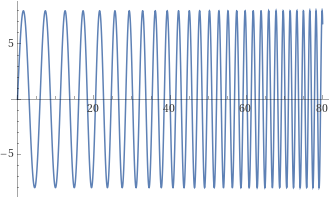
|13|  Accenniamo, ora, ad alcuni approfondimenti.

•  macosa.dima.unige.it/WolframAlpha es.htm:  qui trovate molti esempi d'uso di WolframAlpha nelle varie aree della matematica e nelle altre discipline. Sulla musica in particolare:

www.wolframalpha.com/examples/society-and-culture/arts-and-media/music

•  teorema di Escher

•  orchesta, strumenti, fisica, matematica e musica

•  strumenti  musicali  online  d'uso gratuito ed esempi d'uso.

•  link vari

Se volete, potete, poi, inviarmi dei messaggi di posta elettronica cliccando QUI.