Statistica e Probabilità - 1
•
Nel primo "incontro" abbiamo affrontato alcuni quesiti introduttivi. Tra questi
alcuni erano riferiti alla Statistica e alla Probabilità; si
riferivano ad argomenti di base, che tuttavia in genere non sono affrontati nella scuola superiore. Ma
la statistica e la probabilità sono presenti nel curricolo scolastico? in quali scuole? da quando?
•
Chi di voi non è troppo anziano dovrebbe avere affrontato questi temi in tutti i
livelli scolastici, in quanto essi sono presenti da decine d'anni nei programmi della scuola italiana:
programmi delle elementari (1985);
programmi delle medie (1979) e del primo biennio superiore (Piano
Nazionale Informatica - 1987, Commissione Brocca - 1991). Per tutti i temi (e, quindi, anche per la statistica e
la probabilità) vi è l'indicazione
di non fare uno svolgimento del tema separato dagli altri, ma di intrecciarlo a quello degli altri temi.
Ma questa era la legge, e ben pochi insegnanti e dirigenti scolastici (e case editrici)
l'hanno rispettata (sia nella scelta dei temi da svolgere che nell'impostazione, interdisciplinare e
intradisciplinare, di essi)!!!
E vi era già l'indicazione esplicita di usare i mezzi di calcolo,
che è pressoché indispensabile se si vogliono affrontare problematiche statistiche.
Forse è proprio questo intreccio tra statistica ed uso dei mezzi di calcolo, e la natura
inter- ed intra-disciplinare di queste aree della matematica (che, per altro, avrebbe buttato a mare anche il
modo in cui venivano introdotte l'algebra, la geometria e l'analisi), che ha causato il loro "abbandono" da
parte della maggioranza degli insegnanti (e da parte delle case editrici).
•
Nelle poche ore che abbiamo a disposizione cercheremo di toccare, attraverso alcuni
esercizi (più che con "chiacchiere"), i vari problemi didattici (e le varie opportunità
didattiche) che l'insegnamento di queste aree della matematica pone/offre. Per
semplicità useremo il software standard statistico, R, di cui
qui potete esaminare un help "alfabetico".
L'uso del computer, oltre ad essere indispensabile per analizzare dati "veri", è
utile didatticamente in generale: tutti gli alunni hanno un computer e la scuola "deve" far riferimento
al computer come uno strumento normale con cui fare scuola e con cui gli alunni anche a casa fanno
matematica, fisica, letterartura, greco, scienze, .... In rete c'è molto di più,
e molto migliore, di quanto si può trovare sui libri di testo più diffusi, e "gratuito".
Ma c'è anche di peggio. La scuola deve educare gli alunni all'uso critico di quanto trovano
in rete, perché questo sarà il riferimento culturale degli alunni. In prospettiva
i laboratori informatici spariranno: le scuole (o, meglio, le poche scuole con i presidi che fanno il
loro mestiere) si stanno già attrezzando di proiettori in tutte le classi con cui gli insegnanti
visualizzano le lezioni o i materiali prodotti dagli alunni, che poi vengono messi in rete. Molte
scuole si stanno dotando anche di piccoli computer portatili, in altre li si fa portare agli
alunni, ... Il mondo cambia ... (e, molto lentamente, cambierà anche la scuola: dipende
anche da noi).
# Esegui le seguenti righe di comandi in R, da un blocco di # all'altro
# (vedremo dopo dove/come trovare i vari comandi).
#
# Non trovo le tariffe chilometriche dei treni. Prendo allora in considerazione le
# tariffe InterCity (del 2010) di alcune corse e cerco di capire che relazione c'e'.
# Procedo graficamente ("c" indica una collezione di oggetti, "length" ne dà la
# lunghezza, "plot" traccia, "abline" traccia rette verticali/orizzontali, "axTicks"
# sceglie automaticamente coordinate per tracciare tali rette):
km <- c(28, 46, 90, 144, 165, 313, 501, 769, 1023)
euro <- c(6, 7, 9, 13.50, 16, 24.70, 38.50, 52.50, 72.50)
length(km); length(euro)
# 9 9
plot(km, euro)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
 # Capisco che c'è una relazione più o meno lineare.
# Sceglo io la scala, precisando l'intervallo delle y
plot(km, euro, ylim=c(0,80))
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
abline(v=seq(0,1000,100), h=seq(0,80,5), col="blue",lty=3)
# prendo come pendenza il salto delle "y" diviso quello delle "x"
(euro[9]-euro[1])/(km[9]-km[1])
# approssimo il valore con 0.067 e prendo 4 come intercetta
f <- function(x) 4+0.067*x
plot(f,0,1100,add=TRUE,col="red")
# Capisco che c'è una relazione più o meno lineare.
# Sceglo io la scala, precisando l'intervallo delle y
plot(km, euro, ylim=c(0,80))
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
abline(v=seq(0,1000,100), h=seq(0,80,5), col="blue",lty=3)
# prendo come pendenza il salto delle "y" diviso quello delle "x"
(euro[9]-euro[1])/(km[9]-km[1])
# approssimo il valore con 0.067 e prendo 4 come intercetta
f <- function(x) 4+0.067*x
plot(f,0,1100,add=TRUE,col="red")
 # Vedremo, poi, metodi più sofisticati per approssimare dei punti
# mediante grafici di funzioni.
#
# Altra situazione: i consumi in Italia in anni diversi:
voci <- c("alim","tabac","vest","abitaz","trasp","altro")
a1926 <- c(77749, 3226, 17659, 6849, 3420, 15302) # milioni di lire
a1965 <- c(10213, 734, 2154, 2305, 2014, 6532) # miliardi di lire
a2008 <- c(137460, 17587, 71380, 198404, 120769, 392331) # milioni di euro
barplot(a1926)
# Li ho rappresentati con un diagramma a barre.
# Metto le "voci", un titolo e una griglia "orizzontale" (allargo eventualmente
# la finestra per vedere i nomi delle colonne)
barplot(a1926,names.arg=voci,main="1926")
abline(h=axTicks(2),col="red",lty=3)
# mi conviene rappresentare la distribuzione percentuale,
# causa l'inflazione e il cambio di moneta:
barplot(a1926/sum(a1926)*100,names.arg=voci,main="1926")
abline(h=axTicks(2),col="red",lty=3)
# Potrei fare i grafici in nuove finestre, usando via via "windows":
windows(); barplot(a1965/sum(a1965)*100,names.arg=voci,main="1965")
windows(); barplot(a2008/sum(a2008)*100,names.arg=voci,main="2008")
# ma devo spostare ed eventualmente ridimensionare le finestre. Cancelliamo
# le finestre grafiche costruite e procediamo diversamente.
# Posso fare i grafici in un'unica finestra (1 riga di grafici in 3 colonne,
# con un po' di margini) col comando "par" (modificherò poi col mouse le
# dimensioni della finestra, allargandola e accorciandola); scelgo con "ylim"
# lo stesso intervallo delle "y" in modo da poter confrontare i grafici.
par(mfrow=c(1,3), mar=c(3,3,2,1))
barplot(a1926/sum(a1926)*100,names.arg=voci,main="1926",ylim=c(0,65));abline(h=axTicks(2),col="red",lty=3)
barplot(a1965/sum(a1965)*100,names.arg=voci,main="1965",ylim=c(0,65));abline(h=axTicks(2),col="red",lty=3)
barplot(a2008/sum(a2008)*100,names.arg=voci,main="2008",ylim=c(0,65));abline(h=axTicks(2),col="red",lty=3)
# Vedremo, poi, metodi più sofisticati per approssimare dei punti
# mediante grafici di funzioni.
#
# Altra situazione: i consumi in Italia in anni diversi:
voci <- c("alim","tabac","vest","abitaz","trasp","altro")
a1926 <- c(77749, 3226, 17659, 6849, 3420, 15302) # milioni di lire
a1965 <- c(10213, 734, 2154, 2305, 2014, 6532) # miliardi di lire
a2008 <- c(137460, 17587, 71380, 198404, 120769, 392331) # milioni di euro
barplot(a1926)
# Li ho rappresentati con un diagramma a barre.
# Metto le "voci", un titolo e una griglia "orizzontale" (allargo eventualmente
# la finestra per vedere i nomi delle colonne)
barplot(a1926,names.arg=voci,main="1926")
abline(h=axTicks(2),col="red",lty=3)
# mi conviene rappresentare la distribuzione percentuale,
# causa l'inflazione e il cambio di moneta:
barplot(a1926/sum(a1926)*100,names.arg=voci,main="1926")
abline(h=axTicks(2),col="red",lty=3)
# Potrei fare i grafici in nuove finestre, usando via via "windows":
windows(); barplot(a1965/sum(a1965)*100,names.arg=voci,main="1965")
windows(); barplot(a2008/sum(a2008)*100,names.arg=voci,main="2008")
# ma devo spostare ed eventualmente ridimensionare le finestre. Cancelliamo
# le finestre grafiche costruite e procediamo diversamente.
# Posso fare i grafici in un'unica finestra (1 riga di grafici in 3 colonne,
# con un po' di margini) col comando "par" (modificherò poi col mouse le
# dimensioni della finestra, allargandola e accorciandola); scelgo con "ylim"
# lo stesso intervallo delle "y" in modo da poter confrontare i grafici.
par(mfrow=c(1,3), mar=c(3,3,2,1))
barplot(a1926/sum(a1926)*100,names.arg=voci,main="1926",ylim=c(0,65));abline(h=axTicks(2),col="red",lty=3)
barplot(a1965/sum(a1965)*100,names.arg=voci,main="1965",ylim=c(0,65));abline(h=axTicks(2),col="red",lty=3)
barplot(a2008/sum(a2008)*100,names.arg=voci,main="2008",ylim=c(0,65));abline(h=axTicks(2),col="red",lty=3)
 #
# Altri modi di rappresentare le distribuzioni percentuali (diagrammi a torta):
windows(); pie(a2008, labels=voci, main="2008")
#
# Altri modi di rappresentare le distribuzioni percentuali (diagrammi a torta):
windows(); pie(a2008, labels=voci, main="2008")
 #
# Quali aree della matematica si intrecciano affrontando questi temi?
#
#
# Altre semplici attività affrontabili nel primo biennio
#
# Leggiamo dei dati da rete. Vediamo come sono organizzati
# (leggo le prime 5 righe del file):
readLines("http://macosa.dima.unige.it/om/prg/gfu/altomas.txt", n=5)
# [1] "'record alto maschi dal 32 ogni 4 anni"
# [2] "1932,203"
# [3] "1936,207"
# [4] "1940,209"
# [5] "1944,211"
# C'è una riga iniziale di commenti; i dati sono separati da ","
# Li metto in una tabella, sfruttando queste osservazioni:
hm <- read.table("http://macosa.dima.unige.it/om/prg/stf/altomas.txt",sep=",",skip=1)
# Potrei stamapare la tabella. Facciamolo (lo facciamo come esempio, ma non
# conviene farlo: i dati potrebbero essere migliaia):
hm
# V1 V2
# 1 1932 203
# 2 1936 207
# ...
# 20 2008 245
# Conviene in ogni caso visualizzare solo la struttura dei dati:
str(hm)
# 'data.frame': 20 obs. of 2 variables:
# $ V1: int 1932 1936 1940 1944 1948 1952 1956 1960 1964 1968 ...
# $ V2: int 203 207 209 211 211 211 215 222 228 228 ...
# La tabella non aveva dei nomi per le colonne: sono così state notate V1 e V2
# Carico dati analoghi per le femmine:
readLines("http://macosa.dima.unige.it/om/prg/gfu/altofem.txt", n=1)
hf <- read.table("http://macosa.dima.unige.it/om/prg/stf/altofem.txt",sep=",",skip=1)
str(hf)
# Rappresento i primi dati con plot e poi i successivi con points, in modo che
# non ritracci i nuovi punti ma li aggiunga a quelli tracciati prima. Ma ...
plot(hm,col="blue"); lines(hm); points(hf,col="red")
# ... devo rappresentare i dati in una scala opportuna (come ho già fatto prima):
plot(hm,col="blue",ylim=c(165,250)); lines(hm)
points(hf,col="red"); lines(hf)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
# Per facilitare il confronto conviene rappresentare i numeri indici:
# (che cosa ho rappresentato?)
plot(hm$V1,hm$V2/hm$V2[1]*100, ylim=c(100,130),col="blue",xlab="",ylab="")
lines(hm$V1,hm$V2/hm$V2[1]*100,col="blue")
points(hf$V1,hf$V2/hf$V2[1]*100, col="red",xlab="",ylab="")
lines(hf$V1,hf$V2/hf$V2[1]*100,col="red")
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
# Che cosa visualizzo in più / in meno con le diverse rappresentazioni
# (grafici dei dati originali, grafici dei numeri indici)?
#
# Leggiamo altri dati. Che cosa sono?
readLines("http://macosa.dima.unige.it/om/prg/stf/t-sec.stf", n=5)
# Sono i valori in centesimi di secondo ottenuti da una persona misurando
# manualmente con un orologio il tempo che impiega un altro orologio a
# scattare in avanti di 1 s (le misure sono quindi troncate ai centesimi di
# secondo). La misura vera è dunque 1 sec. Facciamo finta di non conoscerla
# e vediamo come potremmo cercare di determinarla.
# Sono dati singoli, non una tabella di dati. Li carichiamo semplicemente
# usando scan. Salto (con skip) la prima riga.
DATI <- scan("http://macosa.dima.unige.it/om/prg/stf/t-sec.stf", skip=1)
min(DATI); max(DATI); mean(DATI); median(DATI)
# Rappresento i dati con un diagramma a "gambi-foglie" (stem-and-leaf),
# che mi rappresenta graficamente la distribuzione dei dati e, nello stesso
# tempo, mi riporta i dati (una rappresentazione facilmente realizzabile con
# un foglio di carta quadrettata):
stem(DATI)
# Relizziamo anche una rappresentazione con un istogramma:
hist(DATI)
#
# Quali aree della matematica si intrecciano affrontando questi temi?
#
#
# Altre semplici attività affrontabili nel primo biennio
#
# Leggiamo dei dati da rete. Vediamo come sono organizzati
# (leggo le prime 5 righe del file):
readLines("http://macosa.dima.unige.it/om/prg/gfu/altomas.txt", n=5)
# [1] "'record alto maschi dal 32 ogni 4 anni"
# [2] "1932,203"
# [3] "1936,207"
# [4] "1940,209"
# [5] "1944,211"
# C'è una riga iniziale di commenti; i dati sono separati da ","
# Li metto in una tabella, sfruttando queste osservazioni:
hm <- read.table("http://macosa.dima.unige.it/om/prg/stf/altomas.txt",sep=",",skip=1)
# Potrei stamapare la tabella. Facciamolo (lo facciamo come esempio, ma non
# conviene farlo: i dati potrebbero essere migliaia):
hm
# V1 V2
# 1 1932 203
# 2 1936 207
# ...
# 20 2008 245
# Conviene in ogni caso visualizzare solo la struttura dei dati:
str(hm)
# 'data.frame': 20 obs. of 2 variables:
# $ V1: int 1932 1936 1940 1944 1948 1952 1956 1960 1964 1968 ...
# $ V2: int 203 207 209 211 211 211 215 222 228 228 ...
# La tabella non aveva dei nomi per le colonne: sono così state notate V1 e V2
# Carico dati analoghi per le femmine:
readLines("http://macosa.dima.unige.it/om/prg/gfu/altofem.txt", n=1)
hf <- read.table("http://macosa.dima.unige.it/om/prg/stf/altofem.txt",sep=",",skip=1)
str(hf)
# Rappresento i primi dati con plot e poi i successivi con points, in modo che
# non ritracci i nuovi punti ma li aggiunga a quelli tracciati prima. Ma ...
plot(hm,col="blue"); lines(hm); points(hf,col="red")
# ... devo rappresentare i dati in una scala opportuna (come ho già fatto prima):
plot(hm,col="blue",ylim=c(165,250)); lines(hm)
points(hf,col="red"); lines(hf)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
# Per facilitare il confronto conviene rappresentare i numeri indici:
# (che cosa ho rappresentato?)
plot(hm$V1,hm$V2/hm$V2[1]*100, ylim=c(100,130),col="blue",xlab="",ylab="")
lines(hm$V1,hm$V2/hm$V2[1]*100,col="blue")
points(hf$V1,hf$V2/hf$V2[1]*100, col="red",xlab="",ylab="")
lines(hf$V1,hf$V2/hf$V2[1]*100,col="red")
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
# Che cosa visualizzo in più / in meno con le diverse rappresentazioni
# (grafici dei dati originali, grafici dei numeri indici)?
#
# Leggiamo altri dati. Che cosa sono?
readLines("http://macosa.dima.unige.it/om/prg/stf/t-sec.stf", n=5)
# Sono i valori in centesimi di secondo ottenuti da una persona misurando
# manualmente con un orologio il tempo che impiega un altro orologio a
# scattare in avanti di 1 s (le misure sono quindi troncate ai centesimi di
# secondo). La misura vera è dunque 1 sec. Facciamo finta di non conoscerla
# e vediamo come potremmo cercare di determinarla.
# Sono dati singoli, non una tabella di dati. Li carichiamo semplicemente
# usando scan. Salto (con skip) la prima riga.
DATI <- scan("http://macosa.dima.unige.it/om/prg/stf/t-sec.stf", skip=1)
min(DATI); max(DATI); mean(DATI); median(DATI)
# Rappresento i dati con un diagramma a "gambi-foglie" (stem-and-leaf),
# che mi rappresenta graficamente la distribuzione dei dati e, nello stesso
# tempo, mi riporta i dati (una rappresentazione facilmente realizzabile con
# un foglio di carta quadrettata):
stem(DATI)
# Relizziamo anche una rappresentazione con un istogramma:
hist(DATI)
# 6 | 8
# 7 | 8
# 8 | 05
# 9 | 000001466666667778888899
# 10 | 233333699999
# 11 | 00125
# 12 | 19 |  |
# (1) La forma è diversa. Come mai?
# (2) Poi ho ottenuto una media (99.42553) più bassa di quella che mi
# attendevo (un valore più vicino a 100). Come mai?
# Sono problemi comuni, di base, ma che spesso sono trascurati.
# Problema (1): devo specificare come realizzare l'istogramma, ossia se
# classificare i dati in intervalli [,) o in intervalli (,]. Noi, come
# si fa in genere sia in matematica che in fisica, useremo intervalli
# [,) - 7.5 viene arrotondato a 8 in quanto sta in [7.5,8.5), mentre con
# intervalli (,] avremmo scelto 7 in quanto sta in (6.5,7.5].
# La cosa la realizzo così:
hist(DATI,right=FALSE)
# 6 | 8
# 7 | 8
# 8 | 05
# 9 | 000001466666667778888899
# 10 | 233333699999
# 11 | 00125
# 12 | 19 |  |
# Problema (2): questo problema non è legato al software!
# I dati erano tempi in centesimi di secondo, troncati agli interi (cioè ai
# centesimi di secondo).
# Per avere rappresentazioni corrette devo aggiungere 1/2 ad essi:
DATI <- DATI+1/2
min(DATI); max(DATI); mean(DATI); median(DATI)
# Ora ho un valore medio (99.92553) che ha senso!
# La forma dell'istogramma (specie se i dati non sono molti) dipende da
# come si scelgono le classi. Vediamo cosa si ottiene scegliendo diversamente
# le classi:
par(mfrow=c(1,2), mar=c(3,3,2,1))
hist(DATI,right=FALSE,col="yellow",xlab="",ylab="",main="")
hist(DATI,seq(65,135,10),right=FALSE,col="yellow",xlab="",ylab="",main="")
 # Vediamo come avere una sintesi numerica di una sequenza di dati:
summary(DATI)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 68.50 96.50 98.50 99.93 108.00 129.50
# e come associare all'istogramma il relativo box-plot (ed evidenziare
# alcuni percentili con dei "punti") (vedi)
par(mfrow=c(2,1), mar=c(3,3,2,1))
hist(DATI,seq(65,135,10),right=FALSE,col="yellow",xlab="",ylab="",main="")
abline(h=axTicks(2), col="blue",lty=3)
points(min(DATI),0,col="red"); points(quantile(DATI,0.25),0,col="red")
points(max(DATI),0,col="red"); points(quantile(DATI,0.75),0,col="red")
#
boxplot(DATI, horizontal=TRUE, col="yellow",range=0)
points(min(DATI),1,col="red"); points(quantile(DATI,0.25),1,col="red")
points(max(DATI),1,col="red"); points(quantile(DATI,0.75),1,col="red")
points(quantile(DATI,0.05),1,col="blue",pch=19)
points(quantile(DATI,0.95),1,col="blue",pch=19)
# aggiungo una griglia, alta 1/5 del riquadro:
rug(seq(70,130,5),ticksize=0.2)
# Vediamo come avere una sintesi numerica di una sequenza di dati:
summary(DATI)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 68.50 96.50 98.50 99.93 108.00 129.50
# e come associare all'istogramma il relativo box-plot (ed evidenziare
# alcuni percentili con dei "punti") (vedi)
par(mfrow=c(2,1), mar=c(3,3,2,1))
hist(DATI,seq(65,135,10),right=FALSE,col="yellow",xlab="",ylab="",main="")
abline(h=axTicks(2), col="blue",lty=3)
points(min(DATI),0,col="red"); points(quantile(DATI,0.25),0,col="red")
points(max(DATI),0,col="red"); points(quantile(DATI,0.75),0,col="red")
#
boxplot(DATI, horizontal=TRUE, col="yellow",range=0)
points(min(DATI),1,col="red"); points(quantile(DATI,0.25),1,col="red")
points(max(DATI),1,col="red"); points(quantile(DATI,0.75),1,col="red")
points(quantile(DATI,0.05),1,col="blue",pch=19)
points(quantile(DATI,0.95),1,col="blue",pch=19)
# aggiungo una griglia, alta 1/5 del riquadro:
rug(seq(70,130,5),ticksize=0.2)
 # Ecco come avere più boxplot con la stessa scala (utile per valutare
# come evolve una distribuzione di dati nel tempo; qui usiamo dei
# dati inventati):
DATI2 <- DATI*1.1+10; DATI3 <- DATI2*1.1+10; DATI4 <- DATI2*1.1-20
boxplot(DATI,DATI2,DATI3,DATI4,range=0,col="grey")
min(DATI); max(DATI3)
# 68.5 177.695
rug(seq(70,180,10),ticksize=1,side=2,lty=3)
# l'opzione "side=2" specifica che la griglia deve essere verticale
# Ecco come avere più boxplot con la stessa scala (utile per valutare
# come evolve una distribuzione di dati nel tempo; qui usiamo dei
# dati inventati):
DATI2 <- DATI*1.1+10; DATI3 <- DATI2*1.1+10; DATI4 <- DATI2*1.1-20
boxplot(DATI,DATI2,DATI3,DATI4,range=0,col="grey")
min(DATI); max(DATI3)
# 68.5 177.695
rug(seq(70,180,10),ticksize=1,side=2,lty=3)
# l'opzione "side=2" specifica che la griglia deve essere verticale
 #
# Cose varie di calcolo combinatorio
# A ramino (per ogni seme 1,2,…,10,J,Q,K) , quanti sono i modi di fare colore di picche?
choose(13,10)
# 286
# il triangolo di Tartaglia
for(i in 0:10) print(choose(i, 0:i))
# 1
# 1 1
# 1 2 1
# 1 3 3 1
# 1 4 6 4 1
# 1 5 10 10 5 1
# 1 6 15 20 15 6 1
# 1 7 21 35 35 21 7 1
# 1 8 28 56 70 56 28 8 1
# 1 9 36 84 126 126 84 36 9 1
# 1 10 45 120 210 252 210 120 45 10 1
# Con WolframAlpha
#
# modi in cui possono essere vinte le medaglie d'oro, argento, bronzo tra 10 concorrenti
D <- function(n,k) factorial(n)/factorial(n-k); D(10,3)
# 720
#
# Ho costruito un dado con del cartoncino nel modo seguente e ho fatto un po' di
# prove, ottenendo gli esiti seguenti.
#
# Cose varie di calcolo combinatorio
# A ramino (per ogni seme 1,2,…,10,J,Q,K) , quanti sono i modi di fare colore di picche?
choose(13,10)
# 286
# il triangolo di Tartaglia
for(i in 0:10) print(choose(i, 0:i))
# 1
# 1 1
# 1 2 1
# 1 3 3 1
# 1 4 6 4 1
# 1 5 10 10 5 1
# 1 6 15 20 15 6 1
# 1 7 21 35 35 21 7 1
# 1 8 28 56 70 56 28 8 1
# 1 9 36 84 126 126 84 36 9 1
# 1 10 45 120 210 252 210 120 45 10 1
# Con WolframAlpha
#
# modi in cui possono essere vinte le medaglie d'oro, argento, bronzo tra 10 concorrenti
D <- function(n,k) factorial(n)/factorial(n-k); D(10,3)
# 720
#
# Ho costruito un dado con del cartoncino nel modo seguente e ho fatto un po' di
# prove, ottenendo gli esiti seguenti.
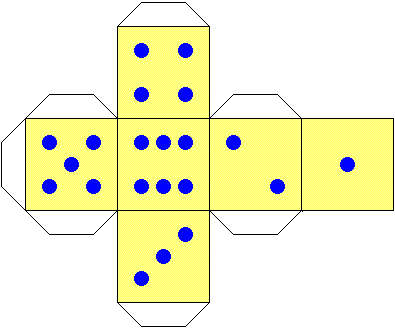 dati <- c(
1,4,6,6,3,3,5,6,2,4,6,2,4,4,2,3,5,2,1,1,5,6,6,1,4,5,4,6,6,5,6,6,4,5,6,2,1,6,
5,3,6,2,6,5,1,6,4,5,5,6,5,2,6,6,6,3,1,4,6,4,2,6,1,6,6,5,4,4,5,5,2,4,6,3,4,2,
5,6,4,3,6,6,1,3,6,2,6,3,6,1,2,2,6,6,3,4,4,2,3,1,4,1,6,4,2,3,1,6,5,1,6,3,5,3,
4,3,2,2,4,4,3,6,3,5,6,6,2,6,6,5,5,5,2,6,1,2,1,4,6,1,4,4,5,3,1,5,4,5,1,2,3,6,
2,2,6,3,3,6,2,6,5,5,1,2,2,4,5,4,5,5,6,1,6,2,5,6,4,4,2,3,5,1,2,2,2,5,4,6,4,5,
1,2,3,2,4,6,3,5,5,6,2,3,2,3,2,6,2,3,6,2,4,6,2,5,3,3,2,2,3,6,5,5,6,5,2,1,4,6,
6,1,1,6,5,2,2,4,4,6,4,3,5,6,3,6,2,4,6,4,5,1,4,2,1,4,2,3,2,1,1,1,4,4,6,5,5,2,
5,1,3,5,1,4,6,3,2,6,1,4,6,3,5,1,6,1,4,6,4,1,2,5,6,4,2,1,2,2,3,1,1,4,3,1,4,5,
2,5,6,6,5,2,5,5,3,2,2,6,5,2,5,1,1,5,6,4,2,3,4,3,3,2,4,6,2,2,5,5,2,5,2,6,3,2,
6,1,2,6,1,2,6,6,2,2,5,5,2,3,6,6,6,3,5,5,6,6,3,4,5,5,4,6,4,5,5,2,2,2,6,6,6,3,
4,5,1,4,3,1,4,1,2,5,1,3,1,3,4,2,3,1,4,4,6,5,5,1,5,2,3,5,2,1,5,6,5,2,2,2,2,5,
6,2,2,3,6,2,1,6,3,3,2,1,1,4,3,3,5,6,5,5,5,6,2,5,1,6,3,6,2,3,6,2,2,2,3,4,2,2,
6,5,4,2,3,1,4,5,6,4,2,3,5,5,3,3,4,3,6,3,2,6,5,2,1,6,5,2,4,4,3,5,3,6,5,6,2,5,
2,5,1,4,4,3,4,5,1,2,2,2,2,1,5,6,4,4,6,3,3,6,1,6,6,6,6,3,6,2,1,1,6,1,2,1,5,6,
2,3,3,2,3,3,1,5,6,2,2,3,1,3,4,4,5,1,5,5,1,1,2,3,5,6,3,3,6,3,1,5,3,4,6,4,2,3,
1,1,2,3,3,5,4,6,5,4,4,6,1,3,5,4,3,2,5,5,5,4,4,2,5,2,6,2,3,6,4,5,2,5,6,1,5,4,
5,4,2,6,3,3,3,6,2,2,4,4,4,3,5,2,5,6,6,6,4,1,6,1,2,2,4,3,1,1,5,4,5,2,4,1,5,6,
2,6,6,3,5,3,1,1,3,6,4,2,4,4,1,5,6,6,5,6,5,3,1,2,2,1,6,2,4,4,1,2,5,2,6,1,2,6,
6,2,4,4,5,5,2,6,6,4,6,4,1,4,3,2,3,6,2,2,3,4,2,6,2,6,6,5,6,4,2,3,5,4,2,5,1,6,
4,1,6,4,6,5,6,5,2,6,6,5,3,6,2,6,6,3,1,4,6,5,2,6,1,6,5,2,4,6,3,4,2,6,5,4,6,5,
5,6,1,4,1,2,6,1,4,3,2,3,6,6,6,6,2,4,2,1,5,6,3,3,1,2,6,5,6,4,6,3,2,5,2,6,5,4
)
length(dati)
# 798
# Quante uscite di 1 mi aspetto più o meno?
# Quant' è la probabilità che esca 1?
# Che cos'è la probabilità che esca 1?
# Che cos'è un dado equo?
# ...
hist(dati,seq(0.5,6.5,1))
dati <- c(
1,4,6,6,3,3,5,6,2,4,6,2,4,4,2,3,5,2,1,1,5,6,6,1,4,5,4,6,6,5,6,6,4,5,6,2,1,6,
5,3,6,2,6,5,1,6,4,5,5,6,5,2,6,6,6,3,1,4,6,4,2,6,1,6,6,5,4,4,5,5,2,4,6,3,4,2,
5,6,4,3,6,6,1,3,6,2,6,3,6,1,2,2,6,6,3,4,4,2,3,1,4,1,6,4,2,3,1,6,5,1,6,3,5,3,
4,3,2,2,4,4,3,6,3,5,6,6,2,6,6,5,5,5,2,6,1,2,1,4,6,1,4,4,5,3,1,5,4,5,1,2,3,6,
2,2,6,3,3,6,2,6,5,5,1,2,2,4,5,4,5,5,6,1,6,2,5,6,4,4,2,3,5,1,2,2,2,5,4,6,4,5,
1,2,3,2,4,6,3,5,5,6,2,3,2,3,2,6,2,3,6,2,4,6,2,5,3,3,2,2,3,6,5,5,6,5,2,1,4,6,
6,1,1,6,5,2,2,4,4,6,4,3,5,6,3,6,2,4,6,4,5,1,4,2,1,4,2,3,2,1,1,1,4,4,6,5,5,2,
5,1,3,5,1,4,6,3,2,6,1,4,6,3,5,1,6,1,4,6,4,1,2,5,6,4,2,1,2,2,3,1,1,4,3,1,4,5,
2,5,6,6,5,2,5,5,3,2,2,6,5,2,5,1,1,5,6,4,2,3,4,3,3,2,4,6,2,2,5,5,2,5,2,6,3,2,
6,1,2,6,1,2,6,6,2,2,5,5,2,3,6,6,6,3,5,5,6,6,3,4,5,5,4,6,4,5,5,2,2,2,6,6,6,3,
4,5,1,4,3,1,4,1,2,5,1,3,1,3,4,2,3,1,4,4,6,5,5,1,5,2,3,5,2,1,5,6,5,2,2,2,2,5,
6,2,2,3,6,2,1,6,3,3,2,1,1,4,3,3,5,6,5,5,5,6,2,5,1,6,3,6,2,3,6,2,2,2,3,4,2,2,
6,5,4,2,3,1,4,5,6,4,2,3,5,5,3,3,4,3,6,3,2,6,5,2,1,6,5,2,4,4,3,5,3,6,5,6,2,5,
2,5,1,4,4,3,4,5,1,2,2,2,2,1,5,6,4,4,6,3,3,6,1,6,6,6,6,3,6,2,1,1,6,1,2,1,5,6,
2,3,3,2,3,3,1,5,6,2,2,3,1,3,4,4,5,1,5,5,1,1,2,3,5,6,3,3,6,3,1,5,3,4,6,4,2,3,
1,1,2,3,3,5,4,6,5,4,4,6,1,3,5,4,3,2,5,5,5,4,4,2,5,2,6,2,3,6,4,5,2,5,6,1,5,4,
5,4,2,6,3,3,3,6,2,2,4,4,4,3,5,2,5,6,6,6,4,1,6,1,2,2,4,3,1,1,5,4,5,2,4,1,5,6,
2,6,6,3,5,3,1,1,3,6,4,2,4,4,1,5,6,6,5,6,5,3,1,2,2,1,6,2,4,4,1,2,5,2,6,1,2,6,
6,2,4,4,5,5,2,6,6,4,6,4,1,4,3,2,3,6,2,2,3,4,2,6,2,6,6,5,6,4,2,3,5,4,2,5,1,6,
4,1,6,4,6,5,6,5,2,6,6,5,3,6,2,6,6,3,1,4,6,5,2,6,1,6,5,2,4,6,3,4,2,6,5,4,6,5,
5,6,1,4,1,2,6,1,4,3,2,3,6,6,6,6,2,4,2,1,5,6,3,3,1,2,6,5,6,4,6,3,2,5,2,6,5,4
)
length(dati)
# 798
# Quante uscite di 1 mi aspetto più o meno?
# Quant' è la probabilità che esca 1?
# Che cos'è la probabilità che esca 1?
# Che cos'è un dado equo?
# ...
hist(dati,seq(0.5,6.5,1))
 hist(dati,seq(0.5,6.5,1),probability=TRUE)
# Qual è la media di queste uscite? Qual è la media "teorica" (o speranza
# matematica o valore atteso) di un dado equo?
mean(dati)
# 3.720551
Dati <- c(1,2,3,4,5,6); mean(Dati)
# 3.5
#
# Come definire la probabiltà? (<- clicca)
# Perchè è sbagliato ed è è dannoso introdurre la probabilità come
# "(casi favorevoli)/(totale dei casi)" ?
#
# Il computer, oltre che per studiare grandi quantità di dati, è utile per simulare
# fenomeni casuali. I vari linguaggi di programmazione hanno incorporato un
# generatore di numeri (pseudo)casuali. In R ha nome runif.
runif(1); runif(1); runif(1)
# vengono generati numeri con valori "casuali" tra 0 ed 1 (che sono
# uniformemente distribuiti, ossia che tendono ad avere la stessa frequenza
# in sottointervalli di eguale ampiezza; tra 0 e 1/3 e tra 2/3 ed 1 abbiamo
# percentuali di uscite che tendono ad eguagliarsi).
# Con runif posso ottenere altri valori casuali, ad es. relativi al lancio
# di un dado (floor è la parte intera):
floor(runif(1)*6)+1; floor(runif(1)*6)+1; floor(runif(1)*6)+1
#
# Opzioni: runif(7) o runif(3,min=1,max=7) generano 7 "numeri casuali" tra
# 0 ed 1 o 3 tra 1 e 7. Ecco come ottenere 25 lanci di un dado equo:
floor(runif(25,min=1,max=7))
#
# Come faccio a controllare che runif generi uscite uniformemente distribuite?
# Con il seguente comando posso vedere, graficamente, come si distribuiscono
# 1000 uscite di runif
hist(runif(1000))
# Se voglio avere le frequenze relative uso il seguente comando, eventualmente
# con probability=TRUE al posto di freq=FALSE
hist(runif(1000),freq=FALSE)
# posso specificare il numero di intervalli:
hist(runif(1000), probability=TRUE, nclass=2)
# All'aumentare il numero delle prove l'istogramma tende ad appiattirsi
hist(runif(1e4),probability=TRUE,nclass=2)
# ma se aumento il numero delle classi ...
hist(runif(1e4),probability=TRUE,nclass=100)
hist(dati,seq(0.5,6.5,1),probability=TRUE)
# Qual è la media di queste uscite? Qual è la media "teorica" (o speranza
# matematica o valore atteso) di un dado equo?
mean(dati)
# 3.720551
Dati <- c(1,2,3,4,5,6); mean(Dati)
# 3.5
#
# Come definire la probabiltà? (<- clicca)
# Perchè è sbagliato ed è è dannoso introdurre la probabilità come
# "(casi favorevoli)/(totale dei casi)" ?
#
# Il computer, oltre che per studiare grandi quantità di dati, è utile per simulare
# fenomeni casuali. I vari linguaggi di programmazione hanno incorporato un
# generatore di numeri (pseudo)casuali. In R ha nome runif.
runif(1); runif(1); runif(1)
# vengono generati numeri con valori "casuali" tra 0 ed 1 (che sono
# uniformemente distribuiti, ossia che tendono ad avere la stessa frequenza
# in sottointervalli di eguale ampiezza; tra 0 e 1/3 e tra 2/3 ed 1 abbiamo
# percentuali di uscite che tendono ad eguagliarsi).
# Con runif posso ottenere altri valori casuali, ad es. relativi al lancio
# di un dado (floor è la parte intera):
floor(runif(1)*6)+1; floor(runif(1)*6)+1; floor(runif(1)*6)+1
#
# Opzioni: runif(7) o runif(3,min=1,max=7) generano 7 "numeri casuali" tra
# 0 ed 1 o 3 tra 1 e 7. Ecco come ottenere 25 lanci di un dado equo:
floor(runif(25,min=1,max=7))
#
# Come faccio a controllare che runif generi uscite uniformemente distribuite?
# Con il seguente comando posso vedere, graficamente, come si distribuiscono
# 1000 uscite di runif
hist(runif(1000))
# Se voglio avere le frequenze relative uso il seguente comando, eventualmente
# con probability=TRUE al posto di freq=FALSE
hist(runif(1000),freq=FALSE)
# posso specificare il numero di intervalli:
hist(runif(1000), probability=TRUE, nclass=2)
# All'aumentare il numero delle prove l'istogramma tende ad appiattirsi
hist(runif(1e4),probability=TRUE,nclass=2)
# ma se aumento il numero delle classi ...
hist(runif(1e4),probability=TRUE,nclass=100)
 # devo aumentare il numero delle uscite
hist(runif(1e6),probability=TRUE,nclass=100)
# devo aumentare il numero delle uscite
hist(runif(1e6),probability=TRUE,nclass=100)
 # Approfondiremo più avanti la riflessione su come "tende" ad appiattirsi.
#
# Non basta vedere che le uscite di runif tendono ad essere distribuite
# uniformemente. Ad es. se voglio simulare il lancio di due dadi o la distribuzione
# di 10 carte di mano in una partita a carte occorre anche che una uscita sia
# indipendente dalle successive. Lo studio di come realizzare un generatore
# di numeri casuali coinvolge molte aree della matematica e non possiamo qui
# approfondire l'argomento. Vediamo solo, per aumentare la nostra convinzione
# che sia un buon generatore, come sono distribuiti 10000x10000 punti generati
# con esso:
plot(c(0,1), c(0,1), type="n", xlab="", ylab="")
points( runif(1e4) ,runif(1e4), pch=".")
# Approfondiremo più avanti la riflessione su come "tende" ad appiattirsi.
#
# Non basta vedere che le uscite di runif tendono ad essere distribuite
# uniformemente. Ad es. se voglio simulare il lancio di due dadi o la distribuzione
# di 10 carte di mano in una partita a carte occorre anche che una uscita sia
# indipendente dalle successive. Lo studio di come realizzare un generatore
# di numeri casuali coinvolge molte aree della matematica e non possiamo qui
# approfondire l'argomento. Vediamo solo, per aumentare la nostra convinzione
# che sia un buon generatore, come sono distribuiti 10000x10000 punti generati
# con esso:
plot(c(0,1), c(0,1), type="n", xlab="", ylab="")
points( runif(1e4) ,runif(1e4), pch=".")
 #
# Per avere un'idea di com'è fatto "runif" vediamo uno dei primi generatori usati
# (1980). In esso compare il simbolo funzionale %% che rappresenta, in R e in molti
# linguaggi di programmazione, la funzione
# mod: (M,N) -> "resto intero della divisione di M per N"
a <- 259; M <- 65536; x0 <- 725
Rand <- function(x) (a*x) %% M
# dividendo per M ho numeri in [0,1)
x <- x0;x/M; x <- Rand(x);x/M; x <- Rand(x);x/M; x <- Rand(x);x/M; x <- Rand(x);x/M
# 0.01106262 0.8652191 0.0917511 0.7635345 0.7554474
# Ovviamente vengono generati un numero finito di punti: è una funzione periodica.
# Vediamo qual è il periodo:
alt <- 0; n <- 1; x <- x0
while(alt == 0) if(Rand(x)==x0) {print(n); alt <- 1} else {x <- Rand(x); n <- n+1}
# ottengo 16384.
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
x <- x0
for(i in 1:3000) {x <- Rand(x); u <- x; x <- Rand(x); points(u/M,x/M,pch=".",cex=2)}
#
# Per avere un'idea di com'è fatto "runif" vediamo uno dei primi generatori usati
# (1980). In esso compare il simbolo funzionale %% che rappresenta, in R e in molti
# linguaggi di programmazione, la funzione
# mod: (M,N) -> "resto intero della divisione di M per N"
a <- 259; M <- 65536; x0 <- 725
Rand <- function(x) (a*x) %% M
# dividendo per M ho numeri in [0,1)
x <- x0;x/M; x <- Rand(x);x/M; x <- Rand(x);x/M; x <- Rand(x);x/M; x <- Rand(x);x/M
# 0.01106262 0.8652191 0.0917511 0.7635345 0.7554474
# Ovviamente vengono generati un numero finito di punti: è una funzione periodica.
# Vediamo qual è il periodo:
alt <- 0; n <- 1; x <- x0
while(alt == 0) if(Rand(x)==x0) {print(n); alt <- 1} else {x <- Rand(x); n <- n+1}
# ottengo 16384.
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
x <- x0
for(i in 1:3000) {x <- Rand(x); u <- x; x <- Rand(x); points(u/M,x/M,pch=".",cex=2)}
 # Bastano queste uscite grafiche per rendersi conto dei limiti di questo generatore
# (e della complessità della questione)
#
# In R si possono impiegare diversi generatori. Anche quello standard (che viene
# impiegato in assenza di specificazioni diverse e risale al 1998) è periodico
# (sono 2^19937-1 numeri che "si ripetono" ...) e può essere impiegato per simulare
# fino a 623 eventi indipendenti!
# Il comando set.seed(n) ("stabilire il seme"), con n numero naturale, fa partire
# la successione "casuale" da un dato valore (con lo stesso n ho la stessa sequenza)
set.seed(7); runif(3); set.seed(7); runif(3)
# 0.9889093 0.3977455 0.1156978 0.9889093 0.3977455 0.1156978
# il "seme" 7 dà luogo, come primo valore casuale, a 0.9889093.
# Generare la stessa successione di numeri "casuali" può essere comodo in molte
# situazioni (testare un algoritmo sulla stessa successione di valori, controllare
# simulazioni di fenomeni, memorizzare codifiche segrete, ...).
# (per inciso, una delle persone che si è occupata molto dei generatori di numeri
# casuali è Knuth, il "papà" di tutta l'area matematico-informatica che si occupa
# dell'analisi degli algoritmi, e che, tra l'altro, nel '78, ha inventato il Teχ).
#
# Dove si può arrivare nel biennio: oltre alle cose viste sopra, c'è almeno un
# altro aspetto educativo importante: vedi (<- clicca).
# Qui l'esempio era riferito ad aspetti sanitari, ma si possono fare esempi in
# altri campi. Nell'esempio abbiamo visto anche un altro aspetto: la possibilità di
# affrontare problemi probabilistici utilizzando grafi o tabelle: è opportuno
# usare entrambe le forme, in modo da dare agli alunni la possibilità di procedere
# come prefersicono (ci sono stili cognitivi diversi: non bisogna imporre a tutti lo
# stile che noi preferiamo).
#
# Ecco, in breve, sintetizzando materiali usati in alcune classi (e togliendo tutti gli
# esercizi che si intrecciavano alla presentazione), come si potrebbero introdurre i
# primi strumenti per descrivere posizione e dispersione dei dati. Vai qui (<- clicca).
#
# Sono argomenti che si intrecciano naturalmente con le prime tecniche di analisi: cambia
# il contesto di riferimento, ma gli strumenti matematici sono sostanzialemnete gli stessi
# (compaiono anche nell'avvio alla sistemazione della fisica, da affrontare a partire dalla
# classe terza).
#
# Ecco, infine, un'avvio al teorema limite centrale, attorno a cui ruota il legame tra
# statistica e probabilità. Vai qui (<- clicca).
#
# Nel prossimo incontro, togliendo un po' di spazio all'ultimo argomento, toccheremo
# la questione delle "coppie di variabili casuali".
#
# Bastano queste uscite grafiche per rendersi conto dei limiti di questo generatore
# (e della complessità della questione)
#
# In R si possono impiegare diversi generatori. Anche quello standard (che viene
# impiegato in assenza di specificazioni diverse e risale al 1998) è periodico
# (sono 2^19937-1 numeri che "si ripetono" ...) e può essere impiegato per simulare
# fino a 623 eventi indipendenti!
# Il comando set.seed(n) ("stabilire il seme"), con n numero naturale, fa partire
# la successione "casuale" da un dato valore (con lo stesso n ho la stessa sequenza)
set.seed(7); runif(3); set.seed(7); runif(3)
# 0.9889093 0.3977455 0.1156978 0.9889093 0.3977455 0.1156978
# il "seme" 7 dà luogo, come primo valore casuale, a 0.9889093.
# Generare la stessa successione di numeri "casuali" può essere comodo in molte
# situazioni (testare un algoritmo sulla stessa successione di valori, controllare
# simulazioni di fenomeni, memorizzare codifiche segrete, ...).
# (per inciso, una delle persone che si è occupata molto dei generatori di numeri
# casuali è Knuth, il "papà" di tutta l'area matematico-informatica che si occupa
# dell'analisi degli algoritmi, e che, tra l'altro, nel '78, ha inventato il Teχ).
#
# Dove si può arrivare nel biennio: oltre alle cose viste sopra, c'è almeno un
# altro aspetto educativo importante: vedi (<- clicca).
# Qui l'esempio era riferito ad aspetti sanitari, ma si possono fare esempi in
# altri campi. Nell'esempio abbiamo visto anche un altro aspetto: la possibilità di
# affrontare problemi probabilistici utilizzando grafi o tabelle: è opportuno
# usare entrambe le forme, in modo da dare agli alunni la possibilità di procedere
# come prefersicono (ci sono stili cognitivi diversi: non bisogna imporre a tutti lo
# stile che noi preferiamo).
#
# Ecco, in breve, sintetizzando materiali usati in alcune classi (e togliendo tutti gli
# esercizi che si intrecciavano alla presentazione), come si potrebbero introdurre i
# primi strumenti per descrivere posizione e dispersione dei dati. Vai qui (<- clicca).
#
# Sono argomenti che si intrecciano naturalmente con le prime tecniche di analisi: cambia
# il contesto di riferimento, ma gli strumenti matematici sono sostanzialemnete gli stessi
# (compaiono anche nell'avvio alla sistemazione della fisica, da affrontare a partire dalla
# classe terza).
#
# Ecco, infine, un'avvio al teorema limite centrale, attorno a cui ruota il legame tra
# statistica e probabilità. Vai qui (<- clicca).
#
# Nel prossimo incontro, togliendo un po' di spazio all'ultimo argomento, toccheremo
# la questione delle "coppie di variabili casuali".
#
 # Capisco che c'è una relazione più o meno lineare.
# Sceglo io la scala, precisando l'intervallo delle y
plot(km, euro, ylim=c(0,80))
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
abline(v=seq(0,1000,100), h=seq(0,80,5), col="blue",lty=3)
# prendo come pendenza il salto delle "y" diviso quello delle "x"
(euro[9]-euro[1])/(km[9]-km[1])
# approssimo il valore con 0.067 e prendo 4 come intercetta
f <- function(x) 4+0.067*x
plot(f,0,1100,add=TRUE,col="red")
# Capisco che c'è una relazione più o meno lineare.
# Sceglo io la scala, precisando l'intervallo delle y
plot(km, euro, ylim=c(0,80))
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
abline(v=seq(0,1000,100), h=seq(0,80,5), col="blue",lty=3)
# prendo come pendenza il salto delle "y" diviso quello delle "x"
(euro[9]-euro[1])/(km[9]-km[1])
# approssimo il valore con 0.067 e prendo 4 come intercetta
f <- function(x) 4+0.067*x
plot(f,0,1100,add=TRUE,col="red")
 # Vedremo, poi, metodi più sofisticati per approssimare dei punti
# mediante grafici di funzioni.
#
# Altra situazione: i consumi in Italia in anni diversi:
voci <- c("alim","tabac","vest","abitaz","trasp","altro")
a1926 <- c(77749, 3226, 17659, 6849, 3420, 15302) # milioni di lire
a1965 <- c(10213, 734, 2154, 2305, 2014, 6532) # miliardi di lire
a2008 <- c(137460, 17587, 71380, 198404, 120769, 392331) # milioni di euro
barplot(a1926)
# Li ho rappresentati con un diagramma a barre.
# Metto le "voci", un titolo e una griglia "orizzontale" (allargo eventualmente
# la finestra per vedere i nomi delle colonne)
barplot(a1926,names.arg=voci,main="1926")
abline(h=axTicks(2),col="red",lty=3)
# mi conviene rappresentare la distribuzione percentuale,
# causa l'inflazione e il cambio di moneta:
barplot(a1926/sum(a1926)*100,names.arg=voci,main="1926")
abline(h=axTicks(2),col="red",lty=3)
# Potrei fare i grafici in nuove finestre, usando via via "windows":
windows(); barplot(a1965/sum(a1965)*100,names.arg=voci,main="1965")
windows(); barplot(a2008/sum(a2008)*100,names.arg=voci,main="2008")
# ma devo spostare ed eventualmente ridimensionare le finestre. Cancelliamo
# le finestre grafiche costruite e procediamo diversamente.
# Posso fare i grafici in un'unica finestra (1 riga di grafici in 3 colonne,
# con un po' di margini) col comando "par" (modificherò poi col mouse le
# dimensioni della finestra, allargandola e accorciandola); scelgo con "ylim"
# lo stesso intervallo delle "y" in modo da poter confrontare i grafici.
par(mfrow=c(1,3), mar=c(3,3,2,1))
barplot(a1926/sum(a1926)*100,names.arg=voci,main="1926",ylim=c(0,65));abline(h=axTicks(2),col="red",lty=3)
barplot(a1965/sum(a1965)*100,names.arg=voci,main="1965",ylim=c(0,65));abline(h=axTicks(2),col="red",lty=3)
barplot(a2008/sum(a2008)*100,names.arg=voci,main="2008",ylim=c(0,65));abline(h=axTicks(2),col="red",lty=3)
# Vedremo, poi, metodi più sofisticati per approssimare dei punti
# mediante grafici di funzioni.
#
# Altra situazione: i consumi in Italia in anni diversi:
voci <- c("alim","tabac","vest","abitaz","trasp","altro")
a1926 <- c(77749, 3226, 17659, 6849, 3420, 15302) # milioni di lire
a1965 <- c(10213, 734, 2154, 2305, 2014, 6532) # miliardi di lire
a2008 <- c(137460, 17587, 71380, 198404, 120769, 392331) # milioni di euro
barplot(a1926)
# Li ho rappresentati con un diagramma a barre.
# Metto le "voci", un titolo e una griglia "orizzontale" (allargo eventualmente
# la finestra per vedere i nomi delle colonne)
barplot(a1926,names.arg=voci,main="1926")
abline(h=axTicks(2),col="red",lty=3)
# mi conviene rappresentare la distribuzione percentuale,
# causa l'inflazione e il cambio di moneta:
barplot(a1926/sum(a1926)*100,names.arg=voci,main="1926")
abline(h=axTicks(2),col="red",lty=3)
# Potrei fare i grafici in nuove finestre, usando via via "windows":
windows(); barplot(a1965/sum(a1965)*100,names.arg=voci,main="1965")
windows(); barplot(a2008/sum(a2008)*100,names.arg=voci,main="2008")
# ma devo spostare ed eventualmente ridimensionare le finestre. Cancelliamo
# le finestre grafiche costruite e procediamo diversamente.
# Posso fare i grafici in un'unica finestra (1 riga di grafici in 3 colonne,
# con un po' di margini) col comando "par" (modificherò poi col mouse le
# dimensioni della finestra, allargandola e accorciandola); scelgo con "ylim"
# lo stesso intervallo delle "y" in modo da poter confrontare i grafici.
par(mfrow=c(1,3), mar=c(3,3,2,1))
barplot(a1926/sum(a1926)*100,names.arg=voci,main="1926",ylim=c(0,65));abline(h=axTicks(2),col="red",lty=3)
barplot(a1965/sum(a1965)*100,names.arg=voci,main="1965",ylim=c(0,65));abline(h=axTicks(2),col="red",lty=3)
barplot(a2008/sum(a2008)*100,names.arg=voci,main="2008",ylim=c(0,65));abline(h=axTicks(2),col="red",lty=3)
 #
# Altri modi di rappresentare le distribuzioni percentuali (diagrammi a torta):
windows(); pie(a2008, labels=voci, main="2008")
#
# Altri modi di rappresentare le distribuzioni percentuali (diagrammi a torta):
windows(); pie(a2008, labels=voci, main="2008")
 #
# Quali aree della matematica si intrecciano affrontando questi temi?
#
#
# Altre semplici attività affrontabili nel primo biennio
#
# Leggiamo dei dati da rete. Vediamo come sono organizzati
# (leggo le prime 5 righe del file):
readLines("http://macosa.dima.unige.it/om/prg/gfu/altomas.txt", n=5)
# [1] "'record alto maschi dal 32 ogni 4 anni"
# [2] "1932,203"
# [3] "1936,207"
# [4] "1940,209"
# [5] "1944,211"
# C'è una riga iniziale di commenti; i dati sono separati da ","
# Li metto in una tabella, sfruttando queste osservazioni:
hm <- read.table("http://macosa.dima.unige.it/om/prg/stf/altomas.txt",sep=",",skip=1)
# Potrei stamapare la tabella. Facciamolo (lo facciamo come esempio, ma non
# conviene farlo: i dati potrebbero essere migliaia):
hm
# V1 V2
# 1 1932 203
# 2 1936 207
# ...
# 20 2008 245
# Conviene in ogni caso visualizzare solo la struttura dei dati:
str(hm)
# 'data.frame': 20 obs. of 2 variables:
# $ V1: int 1932 1936 1940 1944 1948 1952 1956 1960 1964 1968 ...
# $ V2: int 203 207 209 211 211 211 215 222 228 228 ...
# La tabella non aveva dei nomi per le colonne: sono così state notate V1 e V2
# Carico dati analoghi per le femmine:
readLines("http://macosa.dima.unige.it/om/prg/gfu/altofem.txt", n=1)
hf <- read.table("http://macosa.dima.unige.it/om/prg/stf/altofem.txt",sep=",",skip=1)
str(hf)
# Rappresento i primi dati con plot e poi i successivi con points, in modo che
# non ritracci i nuovi punti ma li aggiunga a quelli tracciati prima. Ma ...
plot(hm,col="blue"); lines(hm); points(hf,col="red")
# ... devo rappresentare i dati in una scala opportuna (come ho già fatto prima):
plot(hm,col="blue",ylim=c(165,250)); lines(hm)
points(hf,col="red"); lines(hf)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
# Per facilitare il confronto conviene rappresentare i numeri indici:
# (che cosa ho rappresentato?)
plot(hm$V1,hm$V2/hm$V2[1]*100, ylim=c(100,130),col="blue",xlab="",ylab="")
lines(hm$V1,hm$V2/hm$V2[1]*100,col="blue")
points(hf$V1,hf$V2/hf$V2[1]*100, col="red",xlab="",ylab="")
lines(hf$V1,hf$V2/hf$V2[1]*100,col="red")
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
# Che cosa visualizzo in più / in meno con le diverse rappresentazioni
# (grafici dei dati originali, grafici dei numeri indici)?
#
# Leggiamo altri dati. Che cosa sono?
readLines("http://macosa.dima.unige.it/om/prg/stf/t-sec.stf", n=5)
# Sono i valori in centesimi di secondo ottenuti da una persona misurando
# manualmente con un orologio il tempo che impiega un altro orologio a
# scattare in avanti di 1 s (le misure sono quindi troncate ai centesimi di
# secondo). La misura vera è dunque 1 sec. Facciamo finta di non conoscerla
# e vediamo come potremmo cercare di determinarla.
# Sono dati singoli, non una tabella di dati. Li carichiamo semplicemente
# usando scan. Salto (con skip) la prima riga.
DATI <- scan("http://macosa.dima.unige.it/om/prg/stf/t-sec.stf", skip=1)
min(DATI); max(DATI); mean(DATI); median(DATI)
# Rappresento i dati con un diagramma a "gambi-foglie" (stem-and-leaf),
# che mi rappresenta graficamente la distribuzione dei dati e, nello stesso
# tempo, mi riporta i dati (una rappresentazione facilmente realizzabile con
# un foglio di carta quadrettata):
stem(DATI)
# Relizziamo anche una rappresentazione con un istogramma:
hist(DATI)
#
# Quali aree della matematica si intrecciano affrontando questi temi?
#
#
# Altre semplici attività affrontabili nel primo biennio
#
# Leggiamo dei dati da rete. Vediamo come sono organizzati
# (leggo le prime 5 righe del file):
readLines("http://macosa.dima.unige.it/om/prg/gfu/altomas.txt", n=5)
# [1] "'record alto maschi dal 32 ogni 4 anni"
# [2] "1932,203"
# [3] "1936,207"
# [4] "1940,209"
# [5] "1944,211"
# C'è una riga iniziale di commenti; i dati sono separati da ","
# Li metto in una tabella, sfruttando queste osservazioni:
hm <- read.table("http://macosa.dima.unige.it/om/prg/stf/altomas.txt",sep=",",skip=1)
# Potrei stamapare la tabella. Facciamolo (lo facciamo come esempio, ma non
# conviene farlo: i dati potrebbero essere migliaia):
hm
# V1 V2
# 1 1932 203
# 2 1936 207
# ...
# 20 2008 245
# Conviene in ogni caso visualizzare solo la struttura dei dati:
str(hm)
# 'data.frame': 20 obs. of 2 variables:
# $ V1: int 1932 1936 1940 1944 1948 1952 1956 1960 1964 1968 ...
# $ V2: int 203 207 209 211 211 211 215 222 228 228 ...
# La tabella non aveva dei nomi per le colonne: sono così state notate V1 e V2
# Carico dati analoghi per le femmine:
readLines("http://macosa.dima.unige.it/om/prg/gfu/altofem.txt", n=1)
hf <- read.table("http://macosa.dima.unige.it/om/prg/stf/altofem.txt",sep=",",skip=1)
str(hf)
# Rappresento i primi dati con plot e poi i successivi con points, in modo che
# non ritracci i nuovi punti ma li aggiunga a quelli tracciati prima. Ma ...
plot(hm,col="blue"); lines(hm); points(hf,col="red")
# ... devo rappresentare i dati in una scala opportuna (come ho già fatto prima):
plot(hm,col="blue",ylim=c(165,250)); lines(hm)
points(hf,col="red"); lines(hf)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
# Per facilitare il confronto conviene rappresentare i numeri indici:
# (che cosa ho rappresentato?)
plot(hm$V1,hm$V2/hm$V2[1]*100, ylim=c(100,130),col="blue",xlab="",ylab="")
lines(hm$V1,hm$V2/hm$V2[1]*100,col="blue")
points(hf$V1,hf$V2/hf$V2[1]*100, col="red",xlab="",ylab="")
lines(hf$V1,hf$V2/hf$V2[1]*100,col="red")
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
# Che cosa visualizzo in più / in meno con le diverse rappresentazioni
# (grafici dei dati originali, grafici dei numeri indici)?
#
# Leggiamo altri dati. Che cosa sono?
readLines("http://macosa.dima.unige.it/om/prg/stf/t-sec.stf", n=5)
# Sono i valori in centesimi di secondo ottenuti da una persona misurando
# manualmente con un orologio il tempo che impiega un altro orologio a
# scattare in avanti di 1 s (le misure sono quindi troncate ai centesimi di
# secondo). La misura vera è dunque 1 sec. Facciamo finta di non conoscerla
# e vediamo come potremmo cercare di determinarla.
# Sono dati singoli, non una tabella di dati. Li carichiamo semplicemente
# usando scan. Salto (con skip) la prima riga.
DATI <- scan("http://macosa.dima.unige.it/om/prg/stf/t-sec.stf", skip=1)
min(DATI); max(DATI); mean(DATI); median(DATI)
# Rappresento i dati con un diagramma a "gambi-foglie" (stem-and-leaf),
# che mi rappresenta graficamente la distribuzione dei dati e, nello stesso
# tempo, mi riporta i dati (una rappresentazione facilmente realizzabile con
# un foglio di carta quadrettata):
stem(DATI)
# Relizziamo anche una rappresentazione con un istogramma:
hist(DATI)


 # Vediamo come avere una sintesi numerica di una sequenza di dati:
summary(DATI)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 68.50 96.50 98.50 99.93 108.00 129.50
# e come associare all'istogramma il relativo box-plot (ed evidenziare
# alcuni percentili con dei "punti") (vedi)
par(mfrow=c(2,1), mar=c(3,3,2,1))
hist(DATI,seq(65,135,10),right=FALSE,col="yellow",xlab="",ylab="",main="")
abline(h=axTicks(2), col="blue",lty=3)
points(min(DATI),0,col="red"); points(quantile(DATI,0.25),0,col="red")
points(max(DATI),0,col="red"); points(quantile(DATI,0.75),0,col="red")
#
boxplot(DATI, horizontal=TRUE, col="yellow",range=0)
points(min(DATI),1,col="red"); points(quantile(DATI,0.25),1,col="red")
points(max(DATI),1,col="red"); points(quantile(DATI,0.75),1,col="red")
points(quantile(DATI,0.05),1,col="blue",pch=19)
points(quantile(DATI,0.95),1,col="blue",pch=19)
# aggiungo una griglia, alta 1/5 del riquadro:
rug(seq(70,130,5),ticksize=0.2)
# Vediamo come avere una sintesi numerica di una sequenza di dati:
summary(DATI)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 68.50 96.50 98.50 99.93 108.00 129.50
# e come associare all'istogramma il relativo box-plot (ed evidenziare
# alcuni percentili con dei "punti") (vedi)
par(mfrow=c(2,1), mar=c(3,3,2,1))
hist(DATI,seq(65,135,10),right=FALSE,col="yellow",xlab="",ylab="",main="")
abline(h=axTicks(2), col="blue",lty=3)
points(min(DATI),0,col="red"); points(quantile(DATI,0.25),0,col="red")
points(max(DATI),0,col="red"); points(quantile(DATI,0.75),0,col="red")
#
boxplot(DATI, horizontal=TRUE, col="yellow",range=0)
points(min(DATI),1,col="red"); points(quantile(DATI,0.25),1,col="red")
points(max(DATI),1,col="red"); points(quantile(DATI,0.75),1,col="red")
points(quantile(DATI,0.05),1,col="blue",pch=19)
points(quantile(DATI,0.95),1,col="blue",pch=19)
# aggiungo una griglia, alta 1/5 del riquadro:
rug(seq(70,130,5),ticksize=0.2)
 # Ecco come avere più boxplot con la stessa scala (utile per valutare
# come evolve una distribuzione di dati nel tempo; qui usiamo dei
# dati inventati):
DATI2 <- DATI*1.1+10; DATI3 <- DATI2*1.1+10; DATI4 <- DATI2*1.1-20
boxplot(DATI,DATI2,DATI3,DATI4,range=0,col="grey")
min(DATI); max(DATI3)
# 68.5 177.695
rug(seq(70,180,10),ticksize=1,side=2,lty=3)
# l'opzione "side=2" specifica che la griglia deve essere verticale
# Ecco come avere più boxplot con la stessa scala (utile per valutare
# come evolve una distribuzione di dati nel tempo; qui usiamo dei
# dati inventati):
DATI2 <- DATI*1.1+10; DATI3 <- DATI2*1.1+10; DATI4 <- DATI2*1.1-20
boxplot(DATI,DATI2,DATI3,DATI4,range=0,col="grey")
min(DATI); max(DATI3)
# 68.5 177.695
rug(seq(70,180,10),ticksize=1,side=2,lty=3)
# l'opzione "side=2" specifica che la griglia deve essere verticale
 #
# Cose varie di calcolo combinatorio
# A ramino (per ogni seme 1,2,…,10,J,Q,K) , quanti sono i modi di fare colore di picche?
choose(13,10)
# 286
# il triangolo di Tartaglia
for(i in 0:10) print(choose(i, 0:i))
# 1
# 1 1
# 1 2 1
# 1 3 3 1
# 1 4 6 4 1
# 1 5 10 10 5 1
# 1 6 15 20 15 6 1
# 1 7 21 35 35 21 7 1
# 1 8 28 56 70 56 28 8 1
# 1 9 36 84 126 126 84 36 9 1
# 1 10 45 120 210 252 210 120 45 10 1
# Con WolframAlpha
#
# modi in cui possono essere vinte le medaglie d'oro, argento, bronzo tra 10 concorrenti
D <- function(n,k) factorial(n)/factorial(n-k); D(10,3)
# 720
#
# Ho costruito un dado con del cartoncino nel modo seguente e ho fatto un po' di
# prove, ottenendo gli esiti seguenti.
#
# Cose varie di calcolo combinatorio
# A ramino (per ogni seme 1,2,…,10,J,Q,K) , quanti sono i modi di fare colore di picche?
choose(13,10)
# 286
# il triangolo di Tartaglia
for(i in 0:10) print(choose(i, 0:i))
# 1
# 1 1
# 1 2 1
# 1 3 3 1
# 1 4 6 4 1
# 1 5 10 10 5 1
# 1 6 15 20 15 6 1
# 1 7 21 35 35 21 7 1
# 1 8 28 56 70 56 28 8 1
# 1 9 36 84 126 126 84 36 9 1
# 1 10 45 120 210 252 210 120 45 10 1
# Con WolframAlpha
#
# modi in cui possono essere vinte le medaglie d'oro, argento, bronzo tra 10 concorrenti
D <- function(n,k) factorial(n)/factorial(n-k); D(10,3)
# 720
#
# Ho costruito un dado con del cartoncino nel modo seguente e ho fatto un po' di
# prove, ottenendo gli esiti seguenti.
 dati <- c(
1,4,6,6,3,3,5,6,2,4,6,2,4,4,2,3,5,2,1,1,5,6,6,1,4,5,4,6,6,5,6,6,4,5,6,2,1,6,
5,3,6,2,6,5,1,6,4,5,5,6,5,2,6,6,6,3,1,4,6,4,2,6,1,6,6,5,4,4,5,5,2,4,6,3,4,2,
5,6,4,3,6,6,1,3,6,2,6,3,6,1,2,2,6,6,3,4,4,2,3,1,4,1,6,4,2,3,1,6,5,1,6,3,5,3,
4,3,2,2,4,4,3,6,3,5,6,6,2,6,6,5,5,5,2,6,1,2,1,4,6,1,4,4,5,3,1,5,4,5,1,2,3,6,
2,2,6,3,3,6,2,6,5,5,1,2,2,4,5,4,5,5,6,1,6,2,5,6,4,4,2,3,5,1,2,2,2,5,4,6,4,5,
1,2,3,2,4,6,3,5,5,6,2,3,2,3,2,6,2,3,6,2,4,6,2,5,3,3,2,2,3,6,5,5,6,5,2,1,4,6,
6,1,1,6,5,2,2,4,4,6,4,3,5,6,3,6,2,4,6,4,5,1,4,2,1,4,2,3,2,1,1,1,4,4,6,5,5,2,
5,1,3,5,1,4,6,3,2,6,1,4,6,3,5,1,6,1,4,6,4,1,2,5,6,4,2,1,2,2,3,1,1,4,3,1,4,5,
2,5,6,6,5,2,5,5,3,2,2,6,5,2,5,1,1,5,6,4,2,3,4,3,3,2,4,6,2,2,5,5,2,5,2,6,3,2,
6,1,2,6,1,2,6,6,2,2,5,5,2,3,6,6,6,3,5,5,6,6,3,4,5,5,4,6,4,5,5,2,2,2,6,6,6,3,
4,5,1,4,3,1,4,1,2,5,1,3,1,3,4,2,3,1,4,4,6,5,5,1,5,2,3,5,2,1,5,6,5,2,2,2,2,5,
6,2,2,3,6,2,1,6,3,3,2,1,1,4,3,3,5,6,5,5,5,6,2,5,1,6,3,6,2,3,6,2,2,2,3,4,2,2,
6,5,4,2,3,1,4,5,6,4,2,3,5,5,3,3,4,3,6,3,2,6,5,2,1,6,5,2,4,4,3,5,3,6,5,6,2,5,
2,5,1,4,4,3,4,5,1,2,2,2,2,1,5,6,4,4,6,3,3,6,1,6,6,6,6,3,6,2,1,1,6,1,2,1,5,6,
2,3,3,2,3,3,1,5,6,2,2,3,1,3,4,4,5,1,5,5,1,1,2,3,5,6,3,3,6,3,1,5,3,4,6,4,2,3,
1,1,2,3,3,5,4,6,5,4,4,6,1,3,5,4,3,2,5,5,5,4,4,2,5,2,6,2,3,6,4,5,2,5,6,1,5,4,
5,4,2,6,3,3,3,6,2,2,4,4,4,3,5,2,5,6,6,6,4,1,6,1,2,2,4,3,1,1,5,4,5,2,4,1,5,6,
2,6,6,3,5,3,1,1,3,6,4,2,4,4,1,5,6,6,5,6,5,3,1,2,2,1,6,2,4,4,1,2,5,2,6,1,2,6,
6,2,4,4,5,5,2,6,6,4,6,4,1,4,3,2,3,6,2,2,3,4,2,6,2,6,6,5,6,4,2,3,5,4,2,5,1,6,
4,1,6,4,6,5,6,5,2,6,6,5,3,6,2,6,6,3,1,4,6,5,2,6,1,6,5,2,4,6,3,4,2,6,5,4,6,5,
5,6,1,4,1,2,6,1,4,3,2,3,6,6,6,6,2,4,2,1,5,6,3,3,1,2,6,5,6,4,6,3,2,5,2,6,5,4
)
length(dati)
# 798
# Quante uscite di 1 mi aspetto più o meno?
# Quant' è la probabilità che esca 1?
# Che cos'è la probabilità che esca 1?
# Che cos'è un dado equo?
# ...
hist(dati,seq(0.5,6.5,1))
dati <- c(
1,4,6,6,3,3,5,6,2,4,6,2,4,4,2,3,5,2,1,1,5,6,6,1,4,5,4,6,6,5,6,6,4,5,6,2,1,6,
5,3,6,2,6,5,1,6,4,5,5,6,5,2,6,6,6,3,1,4,6,4,2,6,1,6,6,5,4,4,5,5,2,4,6,3,4,2,
5,6,4,3,6,6,1,3,6,2,6,3,6,1,2,2,6,6,3,4,4,2,3,1,4,1,6,4,2,3,1,6,5,1,6,3,5,3,
4,3,2,2,4,4,3,6,3,5,6,6,2,6,6,5,5,5,2,6,1,2,1,4,6,1,4,4,5,3,1,5,4,5,1,2,3,6,
2,2,6,3,3,6,2,6,5,5,1,2,2,4,5,4,5,5,6,1,6,2,5,6,4,4,2,3,5,1,2,2,2,5,4,6,4,5,
1,2,3,2,4,6,3,5,5,6,2,3,2,3,2,6,2,3,6,2,4,6,2,5,3,3,2,2,3,6,5,5,6,5,2,1,4,6,
6,1,1,6,5,2,2,4,4,6,4,3,5,6,3,6,2,4,6,4,5,1,4,2,1,4,2,3,2,1,1,1,4,4,6,5,5,2,
5,1,3,5,1,4,6,3,2,6,1,4,6,3,5,1,6,1,4,6,4,1,2,5,6,4,2,1,2,2,3,1,1,4,3,1,4,5,
2,5,6,6,5,2,5,5,3,2,2,6,5,2,5,1,1,5,6,4,2,3,4,3,3,2,4,6,2,2,5,5,2,5,2,6,3,2,
6,1,2,6,1,2,6,6,2,2,5,5,2,3,6,6,6,3,5,5,6,6,3,4,5,5,4,6,4,5,5,2,2,2,6,6,6,3,
4,5,1,4,3,1,4,1,2,5,1,3,1,3,4,2,3,1,4,4,6,5,5,1,5,2,3,5,2,1,5,6,5,2,2,2,2,5,
6,2,2,3,6,2,1,6,3,3,2,1,1,4,3,3,5,6,5,5,5,6,2,5,1,6,3,6,2,3,6,2,2,2,3,4,2,2,
6,5,4,2,3,1,4,5,6,4,2,3,5,5,3,3,4,3,6,3,2,6,5,2,1,6,5,2,4,4,3,5,3,6,5,6,2,5,
2,5,1,4,4,3,4,5,1,2,2,2,2,1,5,6,4,4,6,3,3,6,1,6,6,6,6,3,6,2,1,1,6,1,2,1,5,6,
2,3,3,2,3,3,1,5,6,2,2,3,1,3,4,4,5,1,5,5,1,1,2,3,5,6,3,3,6,3,1,5,3,4,6,4,2,3,
1,1,2,3,3,5,4,6,5,4,4,6,1,3,5,4,3,2,5,5,5,4,4,2,5,2,6,2,3,6,4,5,2,5,6,1,5,4,
5,4,2,6,3,3,3,6,2,2,4,4,4,3,5,2,5,6,6,6,4,1,6,1,2,2,4,3,1,1,5,4,5,2,4,1,5,6,
2,6,6,3,5,3,1,1,3,6,4,2,4,4,1,5,6,6,5,6,5,3,1,2,2,1,6,2,4,4,1,2,5,2,6,1,2,6,
6,2,4,4,5,5,2,6,6,4,6,4,1,4,3,2,3,6,2,2,3,4,2,6,2,6,6,5,6,4,2,3,5,4,2,5,1,6,
4,1,6,4,6,5,6,5,2,6,6,5,3,6,2,6,6,3,1,4,6,5,2,6,1,6,5,2,4,6,3,4,2,6,5,4,6,5,
5,6,1,4,1,2,6,1,4,3,2,3,6,6,6,6,2,4,2,1,5,6,3,3,1,2,6,5,6,4,6,3,2,5,2,6,5,4
)
length(dati)
# 798
# Quante uscite di 1 mi aspetto più o meno?
# Quant' è la probabilità che esca 1?
# Che cos'è la probabilità che esca 1?
# Che cos'è un dado equo?
# ...
hist(dati,seq(0.5,6.5,1))
 hist(dati,seq(0.5,6.5,1),probability=TRUE)
# Qual è la media di queste uscite? Qual è la media "teorica" (o speranza
# matematica o valore atteso) di un dado equo?
mean(dati)
# 3.720551
Dati <- c(1,2,3,4,5,6); mean(Dati)
# 3.5
#
# Come definire la probabiltà? (<- clicca)
# Perchè è sbagliato ed è è dannoso introdurre la probabilità come
# "(casi favorevoli)/(totale dei casi)" ?
#
# Il computer, oltre che per studiare grandi quantità di dati, è utile per simulare
# fenomeni casuali. I vari linguaggi di programmazione hanno incorporato un
# generatore di numeri (pseudo)casuali. In R ha nome runif.
runif(1); runif(1); runif(1)
# vengono generati numeri con valori "casuali" tra 0 ed 1 (che sono
# uniformemente distribuiti, ossia che tendono ad avere la stessa frequenza
# in sottointervalli di eguale ampiezza; tra 0 e 1/3 e tra 2/3 ed 1 abbiamo
# percentuali di uscite che tendono ad eguagliarsi).
# Con runif posso ottenere altri valori casuali, ad es. relativi al lancio
# di un dado (floor è la parte intera):
floor(runif(1)*6)+1; floor(runif(1)*6)+1; floor(runif(1)*6)+1
#
# Opzioni: runif(7) o runif(3,min=1,max=7) generano 7 "numeri casuali" tra
# 0 ed 1 o 3 tra 1 e 7. Ecco come ottenere 25 lanci di un dado equo:
floor(runif(25,min=1,max=7))
#
# Come faccio a controllare che runif generi uscite uniformemente distribuite?
# Con il seguente comando posso vedere, graficamente, come si distribuiscono
# 1000 uscite di runif
hist(runif(1000))
# Se voglio avere le frequenze relative uso il seguente comando, eventualmente
# con probability=TRUE al posto di freq=FALSE
hist(runif(1000),freq=FALSE)
# posso specificare il numero di intervalli:
hist(runif(1000), probability=TRUE, nclass=2)
# All'aumentare il numero delle prove l'istogramma tende ad appiattirsi
hist(runif(1e4),probability=TRUE,nclass=2)
# ma se aumento il numero delle classi ...
hist(runif(1e4),probability=TRUE,nclass=100)
hist(dati,seq(0.5,6.5,1),probability=TRUE)
# Qual è la media di queste uscite? Qual è la media "teorica" (o speranza
# matematica o valore atteso) di un dado equo?
mean(dati)
# 3.720551
Dati <- c(1,2,3,4,5,6); mean(Dati)
# 3.5
#
# Come definire la probabiltà? (<- clicca)
# Perchè è sbagliato ed è è dannoso introdurre la probabilità come
# "(casi favorevoli)/(totale dei casi)" ?
#
# Il computer, oltre che per studiare grandi quantità di dati, è utile per simulare
# fenomeni casuali. I vari linguaggi di programmazione hanno incorporato un
# generatore di numeri (pseudo)casuali. In R ha nome runif.
runif(1); runif(1); runif(1)
# vengono generati numeri con valori "casuali" tra 0 ed 1 (che sono
# uniformemente distribuiti, ossia che tendono ad avere la stessa frequenza
# in sottointervalli di eguale ampiezza; tra 0 e 1/3 e tra 2/3 ed 1 abbiamo
# percentuali di uscite che tendono ad eguagliarsi).
# Con runif posso ottenere altri valori casuali, ad es. relativi al lancio
# di un dado (floor è la parte intera):
floor(runif(1)*6)+1; floor(runif(1)*6)+1; floor(runif(1)*6)+1
#
# Opzioni: runif(7) o runif(3,min=1,max=7) generano 7 "numeri casuali" tra
# 0 ed 1 o 3 tra 1 e 7. Ecco come ottenere 25 lanci di un dado equo:
floor(runif(25,min=1,max=7))
#
# Come faccio a controllare che runif generi uscite uniformemente distribuite?
# Con il seguente comando posso vedere, graficamente, come si distribuiscono
# 1000 uscite di runif
hist(runif(1000))
# Se voglio avere le frequenze relative uso il seguente comando, eventualmente
# con probability=TRUE al posto di freq=FALSE
hist(runif(1000),freq=FALSE)
# posso specificare il numero di intervalli:
hist(runif(1000), probability=TRUE, nclass=2)
# All'aumentare il numero delle prove l'istogramma tende ad appiattirsi
hist(runif(1e4),probability=TRUE,nclass=2)
# ma se aumento il numero delle classi ...
hist(runif(1e4),probability=TRUE,nclass=100)
 # devo aumentare il numero delle uscite
hist(runif(1e6),probability=TRUE,nclass=100)
# devo aumentare il numero delle uscite
hist(runif(1e6),probability=TRUE,nclass=100)
 # Approfondiremo più avanti la riflessione su come "tende" ad appiattirsi.
#
# Non basta vedere che le uscite di runif tendono ad essere distribuite
# uniformemente. Ad es. se voglio simulare il lancio di due dadi o la distribuzione
# di 10 carte di mano in una partita a carte occorre anche che una uscita sia
# indipendente dalle successive. Lo studio di come realizzare un generatore
# di numeri casuali coinvolge molte aree della matematica e non possiamo qui
# approfondire l'argomento. Vediamo solo, per aumentare la nostra convinzione
# che sia un buon generatore, come sono distribuiti 10000x10000 punti generati
# con esso:
plot(c(0,1), c(0,1), type="n", xlab="", ylab="")
points( runif(1e4) ,runif(1e4), pch=".")
# Approfondiremo più avanti la riflessione su come "tende" ad appiattirsi.
#
# Non basta vedere che le uscite di runif tendono ad essere distribuite
# uniformemente. Ad es. se voglio simulare il lancio di due dadi o la distribuzione
# di 10 carte di mano in una partita a carte occorre anche che una uscita sia
# indipendente dalle successive. Lo studio di come realizzare un generatore
# di numeri casuali coinvolge molte aree della matematica e non possiamo qui
# approfondire l'argomento. Vediamo solo, per aumentare la nostra convinzione
# che sia un buon generatore, come sono distribuiti 10000x10000 punti generati
# con esso:
plot(c(0,1), c(0,1), type="n", xlab="", ylab="")
points( runif(1e4) ,runif(1e4), pch=".")
 #
# Per avere un'idea di com'è fatto "runif" vediamo uno dei primi generatori usati
# (1980). In esso compare il simbolo funzionale %% che rappresenta, in R e in molti
# linguaggi di programmazione, la funzione
# mod: (M,N) -> "resto intero della divisione di M per N"
a <- 259; M <- 65536; x0 <- 725
Rand <- function(x) (a*x) %% M
# dividendo per M ho numeri in [0,1)
x <- x0;x/M; x <- Rand(x);x/M; x <- Rand(x);x/M; x <- Rand(x);x/M; x <- Rand(x);x/M
# 0.01106262 0.8652191 0.0917511 0.7635345 0.7554474
# Ovviamente vengono generati un numero finito di punti: è una funzione periodica.
# Vediamo qual è il periodo:
alt <- 0; n <- 1; x <- x0
while(alt == 0) if(Rand(x)==x0) {print(n); alt <- 1} else {x <- Rand(x); n <- n+1}
# ottengo 16384.
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
x <- x0
for(i in 1:3000) {x <- Rand(x); u <- x; x <- Rand(x); points(u/M,x/M,pch=".",cex=2)}
#
# Per avere un'idea di com'è fatto "runif" vediamo uno dei primi generatori usati
# (1980). In esso compare il simbolo funzionale %% che rappresenta, in R e in molti
# linguaggi di programmazione, la funzione
# mod: (M,N) -> "resto intero della divisione di M per N"
a <- 259; M <- 65536; x0 <- 725
Rand <- function(x) (a*x) %% M
# dividendo per M ho numeri in [0,1)
x <- x0;x/M; x <- Rand(x);x/M; x <- Rand(x);x/M; x <- Rand(x);x/M; x <- Rand(x);x/M
# 0.01106262 0.8652191 0.0917511 0.7635345 0.7554474
# Ovviamente vengono generati un numero finito di punti: è una funzione periodica.
# Vediamo qual è il periodo:
alt <- 0; n <- 1; x <- x0
while(alt == 0) if(Rand(x)==x0) {print(n); alt <- 1} else {x <- Rand(x); n <- n+1}
# ottengo 16384.
plot(c(0,1),c(0,1),type="n",xlab="", ylab="")
x <- x0
for(i in 1:3000) {x <- Rand(x); u <- x; x <- Rand(x); points(u/M,x/M,pch=".",cex=2)}
 # Bastano queste uscite grafiche per rendersi conto dei limiti di questo generatore
# (e della complessità della questione)
#
# In R si possono impiegare diversi generatori. Anche quello standard (che viene
# impiegato in assenza di specificazioni diverse e risale al 1998) è periodico
# (sono 2^19937-1 numeri che "si ripetono" ...) e può essere impiegato per simulare
# fino a 623 eventi indipendenti!
# Il comando set.seed(n) ("stabilire il seme"), con n numero naturale, fa partire
# la successione "casuale" da un dato valore (con lo stesso n ho la stessa sequenza)
set.seed(7); runif(3); set.seed(7); runif(3)
# 0.9889093 0.3977455 0.1156978 0.9889093 0.3977455 0.1156978
# il "seme" 7 dà luogo, come primo valore casuale, a 0.9889093.
# Generare la stessa successione di numeri "casuali" può essere comodo in molte
# situazioni (testare un algoritmo sulla stessa successione di valori, controllare
# simulazioni di fenomeni, memorizzare codifiche segrete, ...).
# (per inciso, una delle persone che si è occupata molto dei generatori di numeri
# casuali è Knuth, il "papà" di tutta l'area matematico-informatica che si occupa
# dell'analisi degli algoritmi, e che, tra l'altro, nel '78, ha inventato il Teχ).
#
# Dove si può arrivare nel biennio: oltre alle cose viste sopra, c'è almeno un
# altro aspetto educativo importante: vedi (<- clicca).
# Qui l'esempio era riferito ad aspetti sanitari, ma si possono fare esempi in
# altri campi. Nell'esempio abbiamo visto anche un altro aspetto: la possibilità di
# affrontare problemi probabilistici utilizzando grafi o tabelle: è opportuno
# usare entrambe le forme, in modo da dare agli alunni la possibilità di procedere
# come prefersicono (ci sono stili cognitivi diversi: non bisogna imporre a tutti lo
# stile che noi preferiamo).
#
# Ecco, in breve, sintetizzando materiali usati in alcune classi (e togliendo tutti gli
# esercizi che si intrecciavano alla presentazione), come si potrebbero introdurre i
# primi strumenti per descrivere posizione e dispersione dei dati. Vai qui (<- clicca).
#
# Sono argomenti che si intrecciano naturalmente con le prime tecniche di analisi: cambia
# il contesto di riferimento, ma gli strumenti matematici sono sostanzialemnete gli stessi
# (compaiono anche nell'avvio alla sistemazione della fisica, da affrontare a partire dalla
# classe terza).
#
# Ecco, infine, un'avvio al teorema limite centrale, attorno a cui ruota il legame tra
# statistica e probabilità. Vai qui (<- clicca).
#
# Nel prossimo incontro, togliendo un po' di spazio all'ultimo argomento, toccheremo
# la questione delle "coppie di variabili casuali".
#
# Bastano queste uscite grafiche per rendersi conto dei limiti di questo generatore
# (e della complessità della questione)
#
# In R si possono impiegare diversi generatori. Anche quello standard (che viene
# impiegato in assenza di specificazioni diverse e risale al 1998) è periodico
# (sono 2^19937-1 numeri che "si ripetono" ...) e può essere impiegato per simulare
# fino a 623 eventi indipendenti!
# Il comando set.seed(n) ("stabilire il seme"), con n numero naturale, fa partire
# la successione "casuale" da un dato valore (con lo stesso n ho la stessa sequenza)
set.seed(7); runif(3); set.seed(7); runif(3)
# 0.9889093 0.3977455 0.1156978 0.9889093 0.3977455 0.1156978
# il "seme" 7 dà luogo, come primo valore casuale, a 0.9889093.
# Generare la stessa successione di numeri "casuali" può essere comodo in molte
# situazioni (testare un algoritmo sulla stessa successione di valori, controllare
# simulazioni di fenomeni, memorizzare codifiche segrete, ...).
# (per inciso, una delle persone che si è occupata molto dei generatori di numeri
# casuali è Knuth, il "papà" di tutta l'area matematico-informatica che si occupa
# dell'analisi degli algoritmi, e che, tra l'altro, nel '78, ha inventato il Teχ).
#
# Dove si può arrivare nel biennio: oltre alle cose viste sopra, c'è almeno un
# altro aspetto educativo importante: vedi (<- clicca).
# Qui l'esempio era riferito ad aspetti sanitari, ma si possono fare esempi in
# altri campi. Nell'esempio abbiamo visto anche un altro aspetto: la possibilità di
# affrontare problemi probabilistici utilizzando grafi o tabelle: è opportuno
# usare entrambe le forme, in modo da dare agli alunni la possibilità di procedere
# come prefersicono (ci sono stili cognitivi diversi: non bisogna imporre a tutti lo
# stile che noi preferiamo).
#
# Ecco, in breve, sintetizzando materiali usati in alcune classi (e togliendo tutti gli
# esercizi che si intrecciavano alla presentazione), come si potrebbero introdurre i
# primi strumenti per descrivere posizione e dispersione dei dati. Vai qui (<- clicca).
#
# Sono argomenti che si intrecciano naturalmente con le prime tecniche di analisi: cambia
# il contesto di riferimento, ma gli strumenti matematici sono sostanzialemnete gli stessi
# (compaiono anche nell'avvio alla sistemazione della fisica, da affrontare a partire dalla
# classe terza).
#
# Ecco, infine, un'avvio al teorema limite centrale, attorno a cui ruota il legame tra
# statistica e probabilità. Vai qui (<- clicca).
#
# Nel prossimo incontro, togliendo un po' di spazio all'ultimo argomento, toccheremo
# la questione delle "coppie di variabili casuali".
#