 |
Statistica e Probabilità - 2 Algebra (e polinomi)
•
Concludiamo questa rapida panoramica, che ha l'obiettivo, attraverso riflessioni
ed esempi, di far emergere alcuni problemi che, secondo me, è importante
tener presenti nell'impostazione e nello sviluppo dell'isegnamento della matematica
nella scuola superiore. Per brevità di esposizione abbiamo fatto riferimento
anche a del materiale e del software impiegato in qualche scuola. Ma si tratta solo
di esempi, che hanno il fine di suscitare qualche elemento di riflessione e qualche
spunto.
• Domani sera metto in rete il "testo dell'esame"
che affronterete con calma (tre domande a ciascuna delle quali rispondere in mezza
facciata; l'orale, che sarà comune alle altre discipline matematiche, avrà
l'obiettivo di controllare che siate voi ad aver risposto).
• Nella prima metà di questa lezione chiudiamo le considerazioni sugli aspetti statistico-probabilistici con una rapida ricognizione degli argomenti legati al caso bi- e multi-variato (trascurando lo studio di alcune distribuzioni univariate e tutta la tematica dei test statistici).
Statistica e Probabilità - 2
Correlazione tra variabili casuali
Definizioni
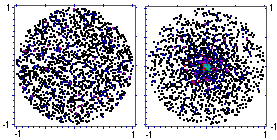
Richiamiamo, velocemente, qualcosa sui sistemi di variabili casuali. Sotto sono rappresentati i punti in cui cadono dei proiettili, lanciati in tre modi diversi. Consideriamo le variabili casuali X ed Y costituite dalle ascisse e dalle ordinate dei punti colpiti. Nel caso a sinistra intuiamo che i punti cadono con distribuzione uniforme nel cerchio di raggio 1 centrato in (0,0). Nel caso al centro intuiamo che i punti tendono a cadere con maggiore frequenza vicino a (0,0), però senza privilegiare alcuna direzione. Nel terzo caso i punti tendono a cadere privilegiando una particolare direzione.
 |
|
|
Si tratta di cadute casuali con diverse leggi di distribuzione.
Qui stiamo estendendo il concetto di legge di distribuzione dal caso di una variabile casuale U a valori
numerici al caso di U = (X,Y) con X e Y variabili casuali a valori in Nel caso discreto (X e Y variabili discrete) la legge di distribuzione
è nota se so calcolare i valori della misura di probabilità Pr su tutti gli eventi del tipo
U =
Per estendere la definizione di probabilità al caso continuo dobbiamo estendere il concetto di integrale
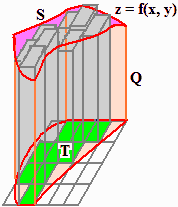
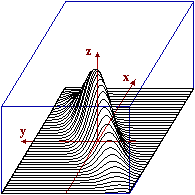
al caso bivariato. Chiamiamo continua una variabile bidimensionale per cui esista una
funzione a 2 input f (funzione di densità) tale che, per ogni evento del
tipo U∈E×F con E e F sottointervalli di I e J (se U varia in I×J):
| 
|
 | 
|
In tutti e tre i casi il valore di X e quello di Y sono tra loro condizionati, ossia non sono stocasticamente indipendenti; ad esempio nei primi due casi X²+Y² deve essere al più 1; se X è vicino ad 1 Y per forza deve essere vicino a 0.
Ma nei primi due casi i punti del bersaglio che vengono colpiti danno luogo a un diagramma di dispersione in cui non viene privilegiata alcuna direzione mentre nel terzo caso i punti tendono a disporsi lungo una linea obliqua, ossia in cui, all'aumentare di X, Y tende ad aumentare più o meno proporzionalmente. Per distinguere queste situazioni, in entrambe delle quali X e Y sono dipendenti, si dice che X e Y nel secondo caso sono correlate, nel primo no.
Per "misurare" la tendenza delle due variabili a variare proporzionalmente si usa il concetto di covarianza, che deriva il suo nome dalla parentela con la formula della varianza: al posto del quadrato dello scarto di una variabile si prende il prodotto dei due scarti:
V(X) = M( (X–M(X))2 )
V(Y) = M( (Y–M(Y))2 ) covarianza: Cov(X,Y) = M( (X–M(X)) (Y–M(Y)) )
Nel caso sperimentale questo termine diventa: Σ i=1..n (Xi–Mn(X))(Yi–Mn(Y)) / n
La formula può essere interpretata come un indicatore che assume un valore assoluto che scende quanto più i punti tendono a disporsi in modo da presentare una simmetria verticale o orizzontale e che cresce quanto più i punti tendono a disporsi lungo una retta obliqua. Infatti le componenti della sommatoria rappresentano aree "con segno" di rettangolini che hanno come dimensioni le distanze "con segno" delle coordinate dei punti dalle coordinate del baricentro. Nella figura sotto a sinistra (simmetria orizzontale) le componenti della sommatoria due a due si annullano, per cui la covarianza è nulla. Se schiaccio obliquamente la nuvola di punti la compensazione diventa solo parziale. Nella caso della figura a destra (X e Y in relazione lineare) non c'è alcuna compensazione (componenti tutte positive) Il segno sarà uguale al segno della pendenza della retta lungo cui i punti tendono a disporsi.
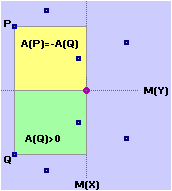
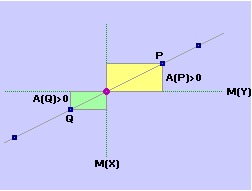
Si può osservare che Cov(X,Y) =
Per non tener conto delle unità di misura in cui sono espressi X e Y (e per passare da un'"area" a un numero puro) la covarianza viene normalizzata dividendo per gli s.q.m. di X e Y, introducendo il:
| coefficiente di correlazione: r X,Y = |
|
= |
|
L'interpretazione geometrica con cui abbiamo introdotto la covarianza fa supporre che se X
e Y sono dipendenti deterministicamente e legate da una relazione lineare Y = aX + b il coefficiente di
correlazione assuma valore assoluto massimo. Ciò può effettivamente essere dimostrato
(la dimostrazione non è complicata, ma la omettiamo).
Si ricava facilmente, usando le proprietà della media, che
in questo caso
Quindi in generale –1 ≤
Un esempio. Limiti e usi distorti della correlazione
A questo punto proviamo ad impiegare R per analizzare coppie (e n-uple) di variabili casuali. Come nel caso "univariato", i dati possono essere introdotti direttamente o essere letti da file, in cui le righe (record) indicano i soggetti su cui si è effettuato il rilevamento e le colonne (campi) indicano le variabili casuali (o modalità) rilevate. Esaminiamo il file battito.txt.
nome <- "http://macosa.dima.unige.it/R/battito.txt"
readLines(nome,n=12)
# Indagine sugli studenti di un corso universitario, dal manuale di MiniTab # battiti prima di eventuale corsa di 1 min # battiti dopo # fatta corsa (1 si`;0 no; a seconda di esito di lancio moneta) # fumatore (1 si`;0 no) # sesso (1 M; 2 F) # altezza # peso # attivita` fisica (0 nulla;1 poca;2 media; 3 molta) Num,BatPrima,BatDopo,Corsa,Fumo,Sesso,Alt,Peso,Fis 01,64,88,1,0,1,168,64,2 02,58,70,1,0,1,183,66,2
In altro formato i dati assumerebbero questo aspetto (non ho messo la prima colonna, che conteneva solo il numero d'ordine):
| bat | bat.dopo | corsa | fumo | sesso | alt | peso | attiv |
| 64 | 88 | 1 | 0 | 1 | 168 | 64 | 2 |
| 58 | 70 | 1 | 0 | 1 | 183 | 66 | 2 |
| ... | ... | ... | ... | ... | ... | ... | ... |
Posso caricare i dati azionando
dati <- read.table(nome,skip=9,header=TRUE,sep =",")
con cui li metto in una tabella, specificando di saltare 9 righe, che c'è un'intestazione
con i nomi dei campi e che i dati sono separati da ",".
Un modo comodo per avere un'idea del file senza stampare tutti i dati (che potrebbero essere molti)
è usare il comando
str(dati)
Con cui ottengo
'data.frame': 92 obs. of 9 variables: $ Num : int 1 2 3 4 5 6 7 8 9 10 ... $ BatPrima: int 64 58 62 66 64 74 84 68 62 76 ... $ BatDopo : int 88 70 76 78 80 84 84 72 75 118 ... $ Corsa : int 1 1 1 1 1 1 1 1 1 1 ... $ Fumo : int 0 0 1 1 0 0 0 0 0 0 ... $ Sesso : int 1 1 1 1 1 1 1 1 1 1 ... $ Alt : int 168 183 186 184 176 184 184 188 184 181 ... $ Peso : int 64 66 73 86 70 75 68 86 88 63 ... $ Fis : int 2 2 3 1 2 1 3 2 2 2 ...
I dati sono stati rilevati durante una lezione di un corso universitario (almeno così viene detto in un manuale del software statistico MiniTab da cui essi sono stati tratti e parzialmente rielaborati – per presentarli nel sistema metrico decimale). La colonna "battiti dopo" si riferisce a un secondo rilevamento del battito cardiaco effettuato dopo che gli studenti a cui (lanciando una moneta) è uscito testa (1 nella colonna "corsa") hanno fatto una corsa di un minuto.
Col comando summary posso avere una informazione sintetica di tutte le variabili; ma la prima colonna contiene solo il numero d'ordine, quindi invece di usare summary(dati) esamino solo le colonne dalla 2 alla 9 con:
summary(dati[2:9])
BatPrima BatDopo Corsa Fumo
Min. : 48.00 Min. : 50 Min. :0.0000 Min. :0.0000
1st Qu.: 64.00 1st Qu.: 68 1st Qu.:0.0000 1st Qu.:0.0000
Median : 71.00 Median : 76 Median :0.0000 Median :0.0000
Mean : 72.87 Mean : 80 Mean :0.3804 Mean :0.3043
3rd Qu.: 80.00 3rd Qu.: 85 3rd Qu.:1.0000 3rd Qu.:1.0000
Max. :100.00 Max. :140 Max. :1.0000 Max. :1.0000
Sesso Alt Peso Fis
Min. :1.00 Min. :154.0 Min. :43.00 Min. :0.000
1st Qu.:1.00 1st Qu.:167.8 1st Qu.:57.00 1st Qu.:2.000
Median :1.00 Median :175.0 Median :66.00 Median :2.000
Mean :1.38 Mean :174.4 Mean :65.84 Mean :2.109
3rd Qu.:2.00 3rd Qu.:183.0 3rd Qu.:70.25 3rd Qu.:2.000
Max. :2.00 Max. :190.0 Max. :97.00 Max. :3.000
Come analizzare un singolo campo e suoi sottocampi:
# definisco una funzione "griglia" per non ripetere sempre le stesse istruzioni
griglia <- function(x) abline(v=axTicks(1), h=axTicks(2), col=x,lty=3)
datiF <- subset(dati,dati$Sesso==2); datiM <- subset(dati,dati$Sesso==1)
h <- dati$Alt; hM <- datiM$Alt; hF <- datiF$Alt
int <- seq(150,200,5); Y <- c(0,0.06)
par(mfrow=c(1,3), mar=c(3,3,2,1))
hist(h,int,right=FALSE,probability=TRUE,ylim=Y,col="grey"); griglia("blue")
hist(hF,int,right=FALSE,probability=TRUE,ylim=Y,col="grey"); griglia("blue")
hist(hM,int,right=FALSE,probability=TRUE,ylim=Y,col="grey"); griglia("blue")
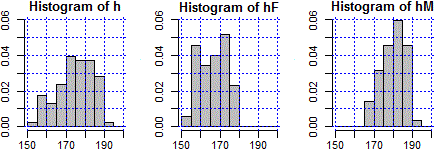
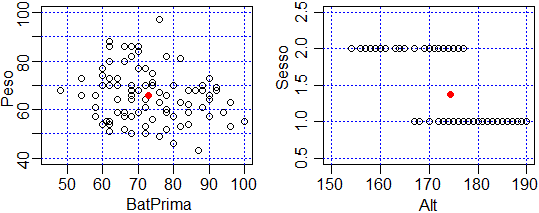
Ecco i diagrammi di dispersione di due coppie di variabili, in un caso entrambe "continue", nell'altro una continua e l'altra discreta; in un caso a bassa correlazione ("nuovola" di punti leggerissimamente inclinata con pendenza negativa), nell'altro ad alta (essendo una discreta, a 2 valori, i punti si distribuiscono su due strisce, ma si vede che l'andamento è "decrescente": correlazione, come vediamo subito dopo, vicina a -1). I punti evidenziati in rosso sono i baricentri dei sistemi di punti rappresentati (alcuni conteggiati più volte).
# Chiudi la finestra precedente o aprine una nuova con windows()
plot(c(45,100),c(40,100),type="n",xlab="BatPrima", ylab="Peso")
griglia("blue")
points(dati$BatPrima,dati$Peso)
points(mean(dati$BatPrima),mean(dati$Peso),pch=19,col="red")
#
plot(c(150,190),c(0.5,2.5),type="n",xlab="Alt", ylab="Sesso")
griglia("blue")
points(dati$Alt,dati$Sesso)
points(mean(dati$Alt),mean(dati$Sesso),pch=19,col="red")
Ecco la matrice di correlazione, che sintetizza le correlazioni tra tutte le diverse variabili di "battito" [avrei potuto battere solo cor(dati[2:9]) ottenendo valori di 8 cifre; con print(…,2) posso "accorciare" i valori; avrei potuto usare, con esiti diversi, round(…,3)]:
print(cor(dati[2:9]),2)
BatPrima BatDopo Corsa Fumo Sesso Alt Peso Fis
BatPrima 1.000 0.616 0.0523 0.129 0.29 -0.211 -0.203 -0.0626
BatDopo 0.616 1.000 0.5768 0.046 0.31 -0.153 -0.166 -0.1411
Corsa 0.052 0.577 1.0000 0.066 -0.11 0.224 0.224 0.0073
Fumo 0.129 0.046 0.0656 1.000 -0.13 0.043 0.201 -0.1202
Sesso 0.285 0.309 -0.1068 -0.129 1.00 -0.709 -0.710 -0.1050
Alt -0.211 -0.153 0.2236 0.043 -0.71 1.000 0.783 0.0893
Peso -0.203 -0.166 0.2240 0.201 -0.71 0.783 1.000 -0.0040
Fis -0.063 -0.141 0.0073 -0.120 -0.10 0.089 -0.004 1.0000
Tra altezza e peso vi è un alto coefficiente di correlazione: 0.78. Se ci restringiamo a una sottopopolazione più omogenea (quella femminile o quella maschile, che hanno pesi e altezze con medie abbastanza diverse), ci potremmo aspettare di ottenere un coefficiente maggiore. Ma se estraiamo la popolazione femminile otteniamo 0.52. Perché?
cor(dati[7],dati[8])
Peso
Alt 0.7826331
cor(subset(dati[7],dati$Sesso==1),subset(dati[8],dati$Sesso==1))
Peso
Alt 0.5904648
cor(subset(dati[7],dati$Sesso==2),subset(dati[8],dati$Sesso==2))
Peso
Alt 0.5191614
Se traccio in rettangoli cartesiani uguali, i grafici di dispersione
par(mfrow=c(1,3), mar=c(3,3,2,1))
plot(c(150,200),c(40,100),type="n",xlab="", ylab=""); griglia("blue")
points(dati$Alt,dati$Peso)
plot(c(150,200),c(40,100),type="n",xlab="", ylab=""); griglia("blue")
points(subset(dati$Alt,dati$Sesso==1),subset(dati$Peso,dati$Sesso==1),col="blue")
plot(c(150,200),c(40,100),type="n",xlab="", ylab=""); griglia("blue")
points(subset(dati$Alt,dati$Sesso==2),subset(dati$Peso,dati$Sesso==2),col="red")
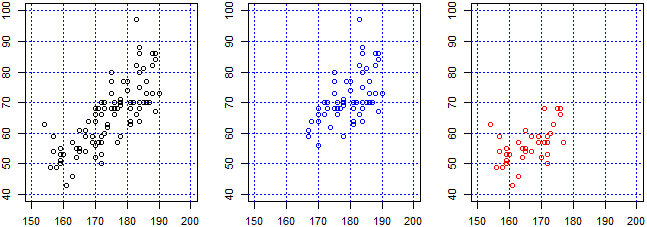
Questo esempio mette in luce come le statistiche che si ottengono sono spesso ingannevoli. In casi come questo, abbastanza frequenti, il problema è dovuto alla presenza di due sottopopolazioni con caratteristiche differenti.
Un altro problema è legato al fatto che le statistiche ottenute su una certa popolazione possono essere utilizzate considerando questa come un campione di una popolazione più estesa. In tal caso alle statistiche ottenute occorre associare degli intervalli di confidenza (nel caso univariato se trovo che una variabile casuale al 68.3% sta nell'intervallo 7.200±0.062, dico che questo è il suo intervallo di confidenza del 68.3%) e, se il campione è piccolo, devono essere opportunamente corrette.
Anche nel caso della covarianza, come in quello della varianza, per avere uno stimatore non distorto del valore riferito alla eventuale popolazione "limite", occorre moltiplicare per n/(n–1), essendo n la numerosità del campione.
La determinazione di intervalli di confidenza è più complicata.
Osserviamo, ad es., che nel caso della correlazione 0.52 tra Altezza e Peso tra le femmine del file "battito" si otterrebbe
[0.22, 0.73] come intervallo di confidenza al 95%, e dovrei tenerne conto se volesi usare questi dati per individuare la
correlazione tra altezza e peso dell'intera popolazione femminile
(se scegliessi una confidenza al 50% otterrei [0.43, 0.60]). Ecco come potrebbe essere svolto questo
calcolo con R:
# devo trasformare le liste dei dati in un puri vettori
x <- subset(dati[7], dati$Sesso==2); x <- unlist(x)
y <- subset(dati[8], dati$Sesso==2); y <- unlist(y)
cor.test(x,y, conf.level = 0.95)
95 percent confidence interval:
0.2248088 0.7266851
sample estimates: cor 0.5191614
Infine (come già osservato nella scorsa lezione), occorre tener conto che quelle individuate sono solo relazioni statistiche, non di causa-effetto: mentre nel caso della correlazione tra le colonne "battito dopo" e "corsa" di "battito" c'è effettivamente una relazione causale (l'aver fatto la corsa influenza il battito cardiaco), il fatto che emerga una correlazione positiva tra il "peso" e l'essere stata sorteggiata la "corsa" non significa che ci sia qualche fattore fisico che faccia sì che l'uscita di testa sia influenzata dalla massa della persona. Purtroppo, specie nei campi medico e socio-psicologico, spesso si fanno collegamenti di questo genere.
Altro ...
Qui ci fermiamo. L'importante era dare un'idea di come si
può affrontare il caso multivariato. Per altri aspetti (la retta e il coefficiente di regressione,
gli assi principali, ...) chi vuole può vedere qui.
Un solo ultimo flash (utile per la "fisica") per accennare al caso non lineare.
Consideriamo un
esempio semplice, che, comunque, si riferisce a situazioni abbastanza diffuse.
Un oggetto, pesante e di forma compatta, viene lasciato cadere e ne viene misurata,
mediante una successione di immagini fotografiche scattate
ogni decimo di secondo, l'altezza in cm da terra. Supponiamo che in corrispondenza
dei tempi di 1, 2, 3, 5 decimi di secondo (rilevati con errori trascurabili)
si registrino, in ordine, le altezze da terra di 131, 113, 89 e 7 centimetri,
arrotondate tutte con la stessa precisone, ad esempio di 1 centimetro.
In situazioni di questo genere, in cui si conoscono le coordinate di N
punti sperimentali con ascisse xi note esattamente e con ordinate yi
della stessa indeterminazione, si può ricorrere ad un procedimento che
impiega tecniche probabilistiche di vario tipo
(che rientrano nella cosiddetta "regressione polinomiale"), per arrivare alla determinazione dei coefficienti
della funzione polinomiale di grado 2 che "con maggiore probabilità" approssima i
punti noti. Senza entrare nei dettagli di esso, si ottiene che si tratta della
funzione
A·N + B·Σxi + C·Σxi2 = Σyi
A·Σxi + B·Σxi2 + C·Σxi3 = Σxiyi
A·Σxi2 + B·Σxi3 + C·Σxi4 = Σxi2yi.
Ecco come fare i calcoli con R.
x <- c(1,2,3,5); y <- c(131,113,89,7) n <- length(x) a <- sum(x); b <- sum(x^2); c <- sum(x^3); d <- sum(x^4) e <- sum(y); f <- sum(x*y); g <- sum(x*x*y) ma <- matrix(data = c(n,a,b,a,b,c,b,c,d), nrow = 3, ncol = 3) noti <- matrix(data = c(e,f,g), nrow = 3, ncol = 1) S <- solve(ma,noti); S # [,1] # [1,] 137.327273 # [2,] -1.945455 # [3,] -4.818182 plot(x,y) abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3) F <- function(x) S[1]+S[2]*x+S[3]*x^2 plot(F,1,5,add=TRUE,col="blue")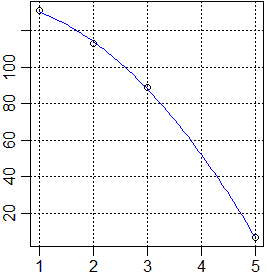
Altro esempio:
x <- c(-5,-2.6,-0.4,2.2,3); y <- c(-1.3,-2.6,-1,4,5.4)Ottengo -0.502079825 1.35599275 0.236170866 | 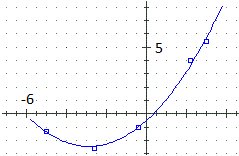 |
Questo era solo un esempio. Esistono numerose tecniche, che dipendono dai modi in cui sono stati raccolti i dati di cui si dispone, dalle altre informazioni che abbiamo sulle funzioni che vogliamo li approssimino, …. Piuttosto che imparare alcune ricette (o adattarsi alle poche elaborazioni che è in grado di fare "direttamente" un foglio di calcolo), è bene, quando si hanno una serie di dati da analizzare, rivolgersi a chi ha effettive esperienze e conoscenze sull'argomento, ed eventualmente usare a "scatola nera" gli strumenti che ci vengono forniti, assieme alle indicazioni su come interpretarne le uscite. L'obiettivo di ogni forma di trasmissione delle conoscenze non è dare delle risposte definitive su tutti gli argomenti trattati, ma dare delle risposte che, spesso, sono parziali e provvisorie, e potranno essere integrate in eventuali studi successivi. È importante rendersi conto di questa incompletezza.
Algebra (e polinomi)
•
Problema da primo biennio di scuola elementare.
Tutti abbiamo messo la stessa cifra, di 2 €. Ci siamo suddivisi una spesa di
30 €. Quanti eravano?
Per quanto devo dividere 30 € in modo da ottenere 2 €?
[è una divisione "per partizione", cioè una suddivisione in parti uguali:
è quella che meglio si presta all'introduzione del concetto di "divisione"; la divisone "per contenenza",
come quella che risolve "ho 30 €, quanti oggetti da 2 € posso comprare?", rappresenta invece un
problema di "moltiplicazione": per quanto devo moltiplicare 2 in modo da ottenere 30; chi fosse
interessato alla problematica dell'avvio alla aritmetica nella scuola elementare può vedere
qui un vecchio articolo elaborato nell'ambito del
dibattito che condusse alla formulazione - in quegli anni - dei nuovi programmi per la scuola elementare]
È il problema "30 diviso N fa 2" per cui trovo la soluzione "N deve esser 15"
[Al livello del primo biennio di scuola elementare la trovo (inizialmente) per "tentativi ragionati":
• • • • • • • • • • |
• • • • • • • • • • |
• • • • • • • • • • 30 diviso 3 fa 10
• • • • • |
• • • • • |
• • • • • |
• • • • • |
• • • • • |
• • • • • 30 diviso 6 fa 5
... Solo successivamente introduco (per le divisoni per partizione) il simbolo ":"; …]
• Un problema da scuola media inferiore, qui, per brevità, presentato e risolto con R:
# Un piccolo gelataio produce e vende un solo tipo di cono, con i seguenti # costi: 0.50 euro di spese incorporate (per latte, cacao, cialde, ...) e # 2000 euro di spese fisse mensili (per locali, energia elettrica, ...) SpeseFisse <- 2000; SpeseIncorporate <- 0.50 # Quanto gli costa un gelato se al mese ne vende N? CostoUnitario <- function(N) SpeseIncorporate + SpeseFisse/N # Se ne traccio il grafico per N tra 0 e 5000 ottengo: plot(CostoUnitario, 0,5000, ylim = c(0,10)) abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3) abline(v=0,h=0)# Quanto deve essere N affinché, se il prezzo di un gelato è 2 euro, il # gelataio non sia in perdita? # Traccio la retta verticale che passa per il punto del grafico con # ordinata 2. abline(h=2,lty=2,col="red") # Ecco come ne trovo la ascissa: # da 2 = SpeseIncorporate+SpeseFisse/N ricavo # 2-SpeseIncorporate = SpeseFisse/N # N = SpeseFisse/(2-SpeseIncorporate) N <- SpeseFisse/(2-SpeseIncorporate); N # Ottengo: 1333.333 (1334) # Ecco come è stata tracciata la retta verticale che ha tale ascissa: abline(v=n,lty=2,col="red")

• Le equazioni
30
/
N = 2
e
2 = SpeseIncorporate +
SpeseFisse
/ N
con incongnita N sono tipiche equazioni da affrontare nella scuola dell'obbligo.
Sono equazioni polinomiali?
Perché in molte scuole secondarie superiori si avvia lo studio della matematica
affrontando i polinomi?
È un retaggio dei vecchi programmi, o è qualcosa di "peggio"?
Vediamo che cosa dicevano i
programmi del 1937.
• Vediamo qualche esempio di ciò che si trova in molti libri. Come comportarci con i colleghi che vorrebbero che insegnassimo queste cose?
Da un diffuso libro di testo: Si chiama monomio ogni funzione che consiste in un prodotto di fattori numerici e di potenze aventi come basi lettere e come esponenti numeri naturali. Si chiama polinomio una somma di due o più monomi.
• Per parlar di polinomi in matematica (la matematica dei matematici
dell'ultimo secolo) occorre specificare la o le indeterminate: si parla di polinomi in x o in x e y o …
• Il polinomio in x
• Al posto di "fattore numerico" occorre usare "costante"
("numerico" vuol dire che rappresenta un numero: una variabile può essere numerica o no;
ad es. può rappresentare una coppia, un vettore, una grandezza fisica, …).
• Al posto di "lettera" occorre usare "variabile" (π è una lettera ma, in genere, è interpretata come una costante; invece in "Area = Lato2" le variabili non sono lettere).
• Viene confuso grossolanamente il concetto di funzione con quello di
termine (x → x+1 e y → y+1 sono la stessa funzione, x+1 e y+1 sono due termini diversi;
le prime indicano come associare ad un oggetto matematico un altro oggetto matematico, le seconde
indicano dei numeri; …: sono confusioni che a noi possono sembrare veniali ma che, se
fatte all'inizio dello studio, conducono ad
atteggiameti fonte di errori su cui poi è difficile intervenire).
• Sono esclusi dalla definizione di monomio le costanti, le singole variabili o termini
del tipo –x (a meno che non si intenda che siano da considerare monomi anche i termini algebricamente
equivalenti a quelli ottenibili con la definizione: ma il libro non intende certo che
5·x·(sin(x)²+cos(x)²), equivalente a 5·x, sia un monomio).
• 5·x, poi, non sarebbe un polinomio (a meno che non lo consideri
equivalente alla somma di monomi 2·x+3·x, ma allora tante altre cose
sono "polinomi" …).
• Poi, quando studierà l'"algebra" dei polinomi, il libro non terrà conto di tutte queste definizioni, ma considererà solo i polinomi in x, anche quelli in cui compaiono altre lettere sotto al segno di frazione o all'interno di una radice quadrata o …!
In molti libri di testo si parla de il massimo comune divisore e il minimo comune multiplo tra polinomi.
Ma non esiste il ... Incredibilmente vengono confuse le operazioni tra polinomi con quelle tra numeri! (tra 2x+2 e 3x²+3x i m.c.d. sono tutti i polinomi kx+k con k numero diverso da 0; si può, eventualmente, scegliere come rappresentate quello "monico", ossia x+1).
A scuola si studiano, spesso, senza particolari distinzioni, i polinomi in una indeterminata e quelli in più.
Ma per i polinomi in più indeterminate non si può definire una divisione con resto, e non si può usare l'algortimo delle divisioni successive per trovare un MCD.
Poi (attreverso sequenza di esercizi stereotipati) vengono fatte incoporporare nella testa degli alunni cose buffe come questa.
Perché?
• Vediamo, a mo' di flash, un esempio di cose da avviare/sistemare al primo anno delle superiori: una di scheda di lavoro estratta da altre in cui, dopo attività e riflessioni operative svolte in vari contesti, si dà una prima sistemazione alle cose: formule per dare nomi agli elementi di una tabella e a come elaborarli, che cos'è un termine, un'equazione, …, ruole delle parentesi, grafi di flusso, "assiomi" di R (senza chiamarli così e formulati in modo opportuno), qualche riflessione storica, … e molti esercizi intercalati alla "teoria".
Qualche riflessione ...
Occorre introdurre/rivedere presto il concetto di
funzione, sotto forma sia di algoritmo che di tabella e di
grafico. Il riferimento a questo concetto entra in
gioco nella definizione dei termini e, quindi, delle formule.
Le riflessioni, di approfondimento e di sintesi, sulla risoluzione
(grafica, numerica e simbolica) di equazioni, sistemi e
disequazioni devono essere volte non tanto alla messa a punto di specifiche
tecniche, quanto alla individuazione di metodi basati sull'uso
di alcuni concetti generali (funzione
inversa, funzione iniettiva, continuità, connettivi logici,
Solo in un secondo tempo va introdotto lo studio delle funzioni polinomiali e delle equazioni polinomiali. Vediamo quali sono gli aspetti che dovrebbero essere messi in luce:
•
le funzioni polinomiali F hanno la caratteristica di avere un andamento del grafico
e i valori delle soluzioni di
•
le funzioni polinomiali sono tutte continue su R;
•
tra i polinomi esiste un'operazione di divisione con resto, che ha varie analogie (ma anche alcune differenze)
con quella tra i numeri interi;
•
il teorema del resto (o di Ruffini);
•
una equazione polinomiale di grado n ha al più n soluzioni;
•
la soluzione di una equazione polinomiale di 2° grado è interpretabile come ricerca
delle intersezioni con l'asse x di una parabola le cui coordinate dipendono
dai coefficienti dell'equazione stessa;
•
è utile memorizzare la scomposizione di alcuni polinomi in polinomi di grado inferiore;
•
perché dedicare tanta attenzione alle funzioni polinomiali?
• Ecco, solo per avere un'idea di quello che si potrebbe fare, una scheda di lavoro che illustra come (in classe seconda) si potrebbero sviluppare i primi argomenti considerati nell'elenco precedente. Diamo una rapida lettura, per avere un'idea degli aspetti concettuali che è importante mettere in luce, e del tipo di esercizi affrontabili (non le equazioni polinomiali di grado 25 o certe strane equazioni "razionali"), con graduazioni diverse a seconda delle classi. Diamo un'occhiata anche al riquadro "grigio" finale.
•
Gli "oggetti" polinomi poi ricompariranno in anni successivi,
in alcuni tipi di scuole. Due flash, per dare un'idea delle cose
che si potrebbero affrontare.
• Un'idea del ruolo delle funzioni polinomiali per
approssimare altre funzioni,
anticipando argomenti che gli alunni che proseguiranno in facoltà scientifiche
(o quelli degli istituti tecnici) affronteranno in futuro.
• Il teorema
fondamentale dell'algebra, con riflessioni storiche sulla nascita del
concetto di numero complesso (e immaginario).