R - 0     R - 1     R - 3

R-0, esempi introduttivi:  funz. di 2 variab,  istogr. e boxplot,  derivate,  grafici di più funzioni.
R-1:  approssimaz.,  frazioni,  num. complessi,  fattoriale,  coeff. binom.,  :,  operatori log.,  ==,  function,  {},  var.locali-globali-parametri,  ifelse,  plot,  abline,  readLines,  read.table,  csv,  dev.new,  ylim,  axTicks,  $,  [ ],  ls,  rm,  c,  length,  range,  sort,  sum,  prod,  seq,  barplot.
R-2:  plot type="n" fg xaxt yaxt,  curve,  add,  copiare comandi ^ v,  help,  ricorsione,  for,  NULL,  min,  max,  quote,  a capo,  seq,  rep,  sort,  mean,  median,  stem-and-leaf,  hist,  [x],  probability=TRUE,  freq=FALSE,  right=FALSE,  main,  par,  mai,  nclass,  colors,  lines,  body,  D,  eval,  integrate.
R-3:  dev.off,  summary,  hist$mids,  hist$density,  sd,  scan,  boxplot,  runif,  floor,  dnorm,  rnorm,  text,  while,  TRUE,  subset,  cor,  lm

R: indice per voci,  WolframAlpha

Attività con R - 2
[righe da eseguire, tra un gurppo di "#" e l'altro]

# Posso rappresentare una parte di piano, ad es. [-4,5]×[-5,8], senza tracciare
# alcun grafico dando a plot da rappresentare il rettangolo [-4,5]×[-5,8] con la
# specificazione type="n"; se non voglio le etichette sugli assi aggiungo xlab=""
# e ylab=""; con fg="white" (foreground) non traccio neanche il box, con xaxt="n"
# e yaxt="n" non traccio neanche i valori di ascisse/ordinate. Un esempio:
#
plot(c(-4,5),c(-5,8),type="n", ylab="", xaxt="n")
#
# Poi posso aggiungervi altre immagini. Vediamo come. Riscelgo la scala e traccio
# i grafici di 3 funzioni a 1 input e 1 output con curve (con cui a differenza che
# con plot non è necessario - ma possibile - specificare il dominio) e l'opzione
# add (per aggiungere il grafico all'immagine precedente, non in un'altra finestra).
#
f <- function(x) x*2-1; g <- function(x) x^2-1; h <- function(x) x/2-1
plot(c(-4,5),c(-5,8),type="n",xlab="", ylab="")
abline(h=0,v=0,col="brown"); abline(v=axTicks(1), h=axTicks(2), col="brown",lty=3)
curve(f, add=TRUE,col="red"); curve(g, add=TRUE,col="blue"); curve(h,add=TRUE)
#
plot(c(-4,5),c(-5,8),type="n",xlab="", ylab="",fg="white")
abline(v=axTicks(1), h=axTicks(2), col="green",lty=3); abline(h=0,v=0,col="brown")
#
plot(c(-4,5),c(-5,8),type="n",xlab="", ylab="",fg="white",xaxt="n",yaxt="n")
abline(h=0,v=0,col="brown"); abline(v=axTicks(1), h=axTicks(2), col="brown",lty=3)
#
# I comandi sono copiabili facilmente e modificabili. Vediamo come.
#
# Schiacciando il tasto freccia ^ [v] si rivedono i preced. [segu.] comandi.
# Quanto fatto può essere memorizzato usando il comando Save History
# e dandogli un nome (con estensione ".Rhistory"). Il file può essere
# ricaricato con Load History e può essere esaminato o caricato con i
# tasti freccia, come detto sopra.
#
# Per esamiare alcune funzioni incorporate si può guardare uno dei vari help; ad
# es. selezionare "R functions (text)" [o "Funzioni di R (testo)], mettere "sqrt"
# come parola da cercare; si apre "MathFun {base}" e da qui si seleziona "Math".
# Si può usare anche "Search Engine & Keywords" attivabile da "Html Help" ("Guida
# Html"), e, soprattutto, sempre da "Html Help", aprire "Packages" e, quindi,
# "Base" e "Graphics". Si tratta, comunque, di help non "facili".    Battendo il
# comando help(sqrt)  si entra direttamente nell'help di sqrt (se non sei in rete
# potrebbe essere azionabile solo "Search Help" - "Cerca nella Guida").
#
# Una definizione per ricorsione:
A <- 90000
F <- function(n) if (n==0) 1 else (Recall(n-1)+A/Recall(n-1))/2
# ovvero: F <- function(n) if (n==1) 1 else (Recall(n-1)+A/Recall(n-1))/2
F(1); F(2); F(10); F(11); F(12)
A <- 1024; F(9); F(10)
# Che cosa calcola F?
# x(0)=1, x(n+1) = ( x(n) + A/x(n) ) / 2 (che converge a ...)

Si può dimostrare che la successione  A(0)=1, A(n+1) = (A(n) + k/A(n)) / 2, con k > 0, convege a √k. Questo è un efficientissimo algoritmo per calcolare la radice quadrata di un numero che risale agli antichi babilonesi. Ha come idea originale la seguente osservazione: se A è una approssimazione per eccesso [difetto] di √k allora k/A ne è una approssimazione per difetto [eccesso] (da A > √k segue che k/A < √k), e quindi come migliore approssimazione si può prendere la media artitmetica, (A+k/A)/2, di tali approssimazioni.

# Se so che un cerchio ha raggio di 5.1 ± 0.1 cm posso calcolarne l'area con:
r <- 5.1 + c(-0.1,0.1); pi*r^2
# Concludo che l'intervallo di indeterminazione è [78.5 cm², 85.0 cm²]
# Per l'ellisse di semiassi di 5.1 ± 0.1 cm e 7.6 ± 0.1 cm posso fare:
r1 <- 5.1 + c(-0.1,0.1); r2 <- 7.6 + c(-0.1,0.1); A <- NULL
for(i in 1:2) for(j in 1:2) A <- c(A, pi*r1[i]*r2[j])
min(A); max(A)
# NULL serve a inizializzare la variabile A, il doppio ciclo for aggiunge via via
# ad A i vari prodotti tra gli estremi dei due intervalli. Le variabili r1, r2 e
# A contengono delle sequenze; per richiamarne un valore devo mettere l'indice
# che lo identifica tra parentesi quadre:
r1; r1[2]; A; A[4]
#
# Un altro esempio: una verifica della terza legge di Keplero
S <- c("mercurio", "venere", "terra")      # nomi satelliti
a <- c(5.791e10, 1.082e11, 1.496e11)       # semiassi maggiori
p <- c(87.969, 224.632, 365.256)*3600*24   # periodi rivoluzione
for(i in 1:3) print( c( S[i], (p^2/a^3)[i] ), quote=FALSE)
# Ho messo in S delle stringhe; con quote=FALSE le stampo senza virgolette.
#
# Se un comando è lungo posso scriverlo tutto su una stessa riga fino a
# qualche migliaio di caratteri o posso andare a capo: la riga seguente è
# interpretata come continuazione (sullo schermo è aggiunto automaticamente
# un "+" all'inizio della nuova riga). Un esempio:
dati <- c(1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20,
         21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40)
mean(dati)
#
# Generazione di alcune sequenze di numeri interi:
s <- 5:11; s; 5:11-1; 5:(11-1); 11:5; s/2
# Più in generale:
seq(6); seq(3,9); seq(3,10,0.8); seq(3,10,len=4); seq(3,by=0.8,len=6)
# modi per ripetere più volte dei dati:
x <- c(3.1, 6.4, 21.7); c(7,rep(x, 4)); c(7,rep(x, each=4))
#
# Analisi dei dati relativi ad un gruppo di alunne quindicenni (altezze in cm)
alu <- c(156,168,162,150,167,157,170,157,159,164,157,165,163,165,166,160,163,162,155)
length(alu); sort(alu); mean(alu); median(alu)
# Stem-and-leaf plot (o, in breve, stem plot). La cifra indicata nella
# prima colonna è il "gambo" (stem) del singolo dato, la cifra rimanente
# è la "foglia" (leaf); per ogni gambo ci possono essere più foglie
# (dati classificati nella stessa classe).
# Quali sono i vantaggi di questo tipo di rappresentazione?
stem(alu)
# Un modo per contare le lunghezze delle colonne, anche parziali
stem(alu, width = 0); stem(alu, width = 2)
# Come scegliere intervalli diversi (lo standard equivale a scale=1)
stem(alu,scale=0.5); stem(alu,scale=3)
#
# Vediamo, ora, come ottenere istogrammi più articolati. Posso battere:
hist(alu)
# Ottengo un istogramma articolato in classi scelte autonomamente da R. Ma conviene
# usare seq per scegliere un certo intervallo (da 140 a 180) e l'ampiezza (5) delle
# classi in cui suddividerlo e classificare i dati in intervalli del tipo [.,.) -
# right=FALSE - come fa automaticamente lo stem:
hist(alu, seq(140,180,5), right=FALSE)
dev.new(); hist(alu, seq(140,180,5), right=TRUE)
# Ho fatto gli istogrammi in due finestre diverse, che posso spostare o
# ridimensionare. Chiudiamole entrambe cliccando [x].
#
# Ecco l'istogramma in intervalli di altra ampiezza, colorato, senza scritte
# (con main posso inserire un titolo alternativo, anche 'vuoto'):
hist(alu,seq(150,171,3),right=FALSE,col="yellow",xlab="",ylab="",main="")
#
# Posso ridurre il margine dei grafici usando il comando par (PARametri grafici)
# con l'opzione mai (MArgini Interni, in pollici). Posso far gestire al software
# l'istogramma specificando con nclass più o meno in quanti intervalli
# classificare i dati [viene scelto un n. di classi tale che esse siano ampie 1,
# 2 o 5 volte una potenza di 10]:
par( mai = c(0.5,0.5,0.1,0.1) )
hist(alu,nclass=8,right=FALSE,col="yellow",xlab="",main="")
#
# Aggiungendo l'opzione  probability=TRUE (o freq=FALSE) posso rappresentare le
# densità, ossia il rapporto tra le frequenze e le ampiezze delle classi:
hist(alu,nclass=8,right=FALSE,col="yellow",xlab="",main="",probability=TRUE)
#
# Posso far tracciare anche l'istogramma in classi di diverse ampiezze (sulla
# scala verticale appare la densità; perché?); devo scegliere in ogni caso
# l'ultimo estremo maggiore strettamente del massimo (170 nel nostro caso)
# per avere un istogramma "corretto".
hist(alu,c(150,156,159,162,168,171),right=FALSE,xlab="",main="")
#
# Ritorneremo successivamente sugli strumenti con cui analizzare dati statistici.
#
# Abbiamo anche visto come il parametro "col" consente di scegliere il colore con
# cui realizzare i grafici.
# I colori usabili sono centinaia; i nomi sono elencati dal comando colors(); non
# mettere il colore è come scegliere black. Eccone alcuni: white yellow yellow3
# yellow4 green green4 violet purple  pink coral  red  magenta magenta4 orange
# brown cyan cyan4 blue blue4  grey grey50 black (i colori sono chiamabili anche
# usando le coordinate RossoVerdeBlu: vedi)
#
# Ecco come aggiungere (al grafico di g <- function(x) x^2-1) la curva
# y^2/10+1 = x tracciata mediante 2000 segmentini:  lines(p,q,...) traccia
# l'insieme dei segmenti con vertici i punti (p,q) dove p e q sono i valori
# descritti in funzione di t, con t che varia tra t1 e t2.
# (perché non posso tracciare la seconda curva con "plot" o "curve"?)
plot(c(-4,5),c(-4,8),type="n",xlab="",ylab="", asp=1)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
abline(v=0, h=0, col="blue",lty=2)
g <- function(x) x^2-1; curve(g, col="brown", add=TRUE)
t1 <- -4; t2 <- 8; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(g(t), t, col="orange")
#
# Due rapidi cenni a come si calcolano le derivate e gli integrali definiti.
f <- function(x) x^2+x^3+sin(2*x)
# Il termine f(x):
body(f)
# Posso derivare il termine  body(f)  specificando qual è la variabile di input:
D(body(f),"x"); D(D(body(f),"x"),"x"); D(D(D(body(f),"x"),"x"),"x")
# Devo usare la stessa variabile di input usata nella definizione:
g <- function(a) cos(2*a)
D(body(g), "a")
# Come definire la funzione derivata? Uso eval (calcola il valore di espressioni):
Df <- function(x) eval(D(body(f),"x"))
Df(3)
# Confronto col calcolo del "rapporto incrementale":
R <- function(x0,h) (f(x0+h)-f(x0))/h
R(3, 1e-1); R(3, 1e-2); R(3, 1e-3); R(3,1e-4); R(3,1e-5); R(3,1e-6); R(3,1e-7)
#
# Gli integrali definiti
g <- function(x) (x-1/2)^2
integrate(g, 0,1)
# Se specifichiamo di voler avere solo il valore:
integrate(g, 0,1)$value
# Per avere il risultato sotto forma di frazione:
library(MASS); fractions( integrate(g, 0,1)$value )
#
# con WolframAlpha:
# integrate (x-1/2)^2 from x=0 to 1
#
# Qual è l'integrale tra 0 e ∞ di x -> exp(-x)?
h <- function(x) exp(-x)
integrate(h, 0,Inf)
#
# Come fa il calcolo? Un "possibile" modo:
   
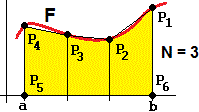# Area che sta tra il grafico di una funzione limitata e continua a tratti e
# l'asse delle x, per x che varia tra a e b, approssimando il grafico con una
# poligonale ad N lati.  Qui il grafico è fatto per punti, così da rappresentare
# correttamente anche le funz. discontinue.  Se aggiungo il comando  grafico <- 0
# viene svolto solo il calcolo (per N grande conviene).
# Svolgendo gli esempi successivi si capisce come opera questa function
grafico <- 1
area <- function(F,a,b,N) {
   n <- N+1; x <- seq(b,a,len=n); y <- F(x)
   # suddivido [b,a] in N parti di estremi x[1]..x[n], prendo gli output y[i]
   # aggiungo x[n+1]=a e x[n+2]=b con ordinata sull'asse x: y[n+1]=y[n+2]=0
   x <- c(x,a,b); y <- c(y,0,0); n <- n+2
   if(grafico == 1) {
   plot(F,a,b, n=5000, type="p", pch=".", asp=1)
   abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
   for(i in 1:n) { points(x[i],y[i],pch=20,col="red")
     lines(c(x[i],x[i+1]),c(y[i],y[i+1]),col="red",lty=2)}
   }
   A <- (y[n]+y[1])*(x[n]-x[1])
   for(i in 1:(n-1)) A <- A + (y[i]+y[i+1])*(x[i]-x[i+1])
   A/2 }  # ho calcolato la somma delle aree degli N trapezi
#
# esempio:
g <- function(x) ifelse(x<=2, x^2, x)
area(g,0,4, 1)
# Ho provato con la poligonale ad 1 lato. Ora aumento il n. dei lati:
area(g,0,4, 10)
area(g,0,4, 1e2)
area(g,0,4, 1e3)
# intuisco che è 8.6 e rotti; evito di rifare il grafico
grafico <- 0
area(g,0,4, 1e4)
area(g,0,4, 1e5)
area(g,0,4, 1e6)
# intuisco che potrebbe essere 8.666…
# Fermiamoci qui.