→ more ←

XX Convegno U.M.I.-C.I.I.M. sull'Insegnamento della Matematica - Orvieto 1998

LE APPLICAZIONI DELLA MATEMATICA NEI CURRICOLI:
finalità, modalità, discipline e contesti coinvolti

Carlo Dapueto
Dipartimento di Matematica dell'Università di Genova

01   In questo intervento, attraverso esempi riferiti ad aree matematiche differenti e a interazioni con diverse aree disciplinari, cercherò di mettere a fuoco i principali aspetti della problematica annunciata nel titolo.

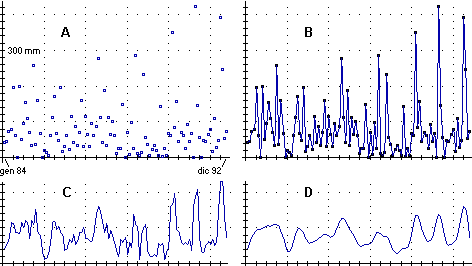
02   Il primo esempio è introdotto dalla figura seguente:

   In A sono rappresentati i millimetri mensili di pioggia a Genova in un certo arco di anni. In B, per migliorare la "lettura" della evoluzione del fenomeno, si sono congiunti i punti mediante segmenti. In C, per "interpretare" meglio i dati (individuare tendenze, ciclicità, …), si sono rappresentate le loro medie mobili: al posto di x(i) si è considerato M(x(i-1), x(i), x(i+1)). D è stato ottenuto iterando 5 volte questo procedimento. A-D sono tutti modelli descrittivi, più o meno astratti, dello stesso fenomeno.

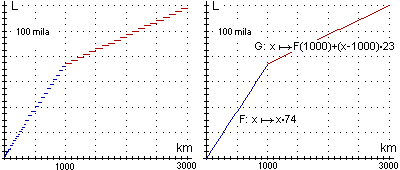
03   Nella successiva figura, a sinistra, sono rappresentate le tariffe ferroviarie (di 2a classe) in vigore in Italia all'inizio del '96. A destra la funzione a scalini è stata approssimata con una funzione continua lineare a tratti. Il modello grafico (a sinistra) mi ha consentito di individuare la regolarità dell'andamento. Il modello analitico ottenuto (a destra) non solo costituisce una modellizzazione concisa del tariffario, ma rivela la logica soggiacente alla definizione delle tariffe: quest'ultimo modello matematico è in realtà il tariffario iniziale, che poi è stato discretizzato per motivi contabili e di comunicazione.

   In altre parole, con il "modello descrittivo" abbiamo esplorato il "modello normativo", ossia la matematica incorporata nel tarriffario.

04   La sovrapposizione di aspetti normativi e descrittivi è tipica dei rapporti tra matematica e altre discipline: economia, fisica (con alcune specificità), informatica, scienze naturali, … .

   Dagli esempi introduttivi emergono anche alcuni aspetti del ruolo del computer nelle attività di matematizzazione (facilitare la rappresentazione e/o i calcoli, la verifica e correzione del modello approssimante, …).

05   Concetto chiave nei rapporti tra matematica e altre discipline è quello di modello, inteso non come particolarizzazione/esemplificazione (i "campioni", la struttura dei numeri interi come modello della teoria dei gruppi, …), ma in quello, duale, di astrazione/idealizzazione (le riproduzioni in scala, la teoria dei gruppi come modello che astrae aspetti che accomunano molte strutture matematiche, …), schematizzabile nel modo seguente:

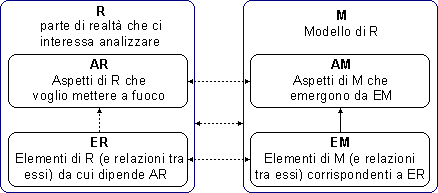
   Nel caso della modellizzazione a destra nella figura in 03, R è il tariffario, AR è il modo in cui il prezzo cresce al crescere della percorrenza, gli elementi ER che abbiamo individuato come significativi nel determinare AR sono costituiti dalle inclinazioni dei tratti rettilinei lungo cui tendono a disporsi i segmentini che costituiscono la rappresentazione grafica del tarriffario; ad esse abbiamo associato come EM le pendenze 74 e 23. AM è la funzione che a x associa F(x) se x≤1000, G(x) altrimenti. Le frecce sono tratteggiate in quanto sono frutto di semplificazioni o approssimazioni (nella scelta di ER abbiamo trascurato l'articolazione in scaglioni del tariffario, nella valutazione degli EM abbiamo fatto delle approssimazioni); EM  AM non è tratteggiata: la funzione dipende esattamente dalle pendenze 74 e 23.

   Nel caso della "regola grammaticale" «per formare la 1a persona dell'imperfetto applica la riscrittura -are  -avo» si tratta di un modello (che utilizziamo per orientarci nella comunicazione verbale) che ha come R il comportamento linguistico degli italiani. La scelta delle parti finali dei verbi e dei loro cambiamenti come ER è una semplificazione: le eccezioni (fare  facevo) testimoniano il fatto che si sono trascurati altri aspetti, ad esempio legati all'origine delle parole (fare segue la seconda coniugazione come il latino facere).

   Anche vari schemi di ragionamento diffusi nell'ambiente scolastico, come «X "sbaglia i calcoli", quindi non è portato per la matematica», sono dei modelli. In questo caso la scelta della destrezza nei calcoli come elemento caratterizzante la bravura in matematica non è tanto frutto di una approssimazione o semplificazione, quanto di una profonda incomprensione della natura della matematica.

06   Non esiste il modello migliore:

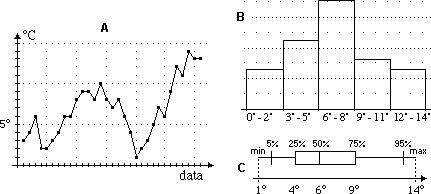D: media = 6.7°   E: mediana = 6°

A-E sono modelli diversi dello stesso fenomeno (il regime termico in un certo mese di una certa località). Il modello A consente di ricostruire l'andamento temporale. B perde la storia ma evidenzia la distribuzione delle temperature e permette di confrontarla con quella di altri mesi o località. Il box-plot C è più compatto e include una quantificazione della dispersione delle temperature, ma perde alcune delle informazioni presenti in B. I modelli D ed E sono molto più sintetici, facilitano il confronto con altri mesi o altre località, ma perdono ogni informazione sia sulla storia che sulla distribuzione.

07   Una disciplina è caratterizzata essenzialmente dall'area fenomenologica per la quale mette a punto modelli (e linguaggi e teorie per elaborare questi modelli).

   La matematica, anche se per lungo tempo si è presentata soprattutto come linguaggio della fisica (le definizioni e le dimostrazioni nella geometria di Euclide erano basate su concetti e argomentazioni di tipo fisico, i concetti di funzione e di continuità inizialmente sono stati lasciati alla intuizione fisica, …), oggi ha la specificità di caratterizzarsi (e di articolarsi internamente) non per gli ambiti applicativi ma essenzialmente per la tipologia degli strumenti di modellizzazione che mette a punto. E più delle altre discipline presenta attività di modellizzazione interna: il concetto di "gruppo" è un modello (M) che ha come realtà (R) strutture matematiche, la "logica" mette a punto modelli che hanno come realtà metodi e linguaggi matematici, … . Sta in questa astrattezza la potenza applicativa della matematica.

   Che cosa facciamo percepire, nell'insegnamento, di tali intrecci e tali differenziazioni?

08   I concetti matematici sono in genere presentati come cose da studiare piuttosto che come modelli (interni o esterni). Quando si fa riferimento a dei contesti ciò avviene quasi solo nell'ambito di problemi stereotipati, in cui la matematizzazione (in particolare l'associazione ER  EM) è caricaturale (le situazioni sono solo messaggi per evocare problemi formalizzati, gli oggetti reali sono nomi a cui associare in base all'esperienza scolastica, senza una riflessione contestuale, oggetti matematici). A volte, nel motivare l'introduzione di un nuovo argomento matematico, si premette l'illustrazione, esplicitamente semplificata, di un problema "reale", ma in genere è trascurata la fase iniziale della modellizzazione (la delimitazione di AR).

   Mentre l'insegnante di matematica tende a strumentalizzare i contesti per fare della "matematica", quello di altre materie tende a far usare acriticamente tecniche e concetti matematici, sviluppando un ricettario che ad ogni problema (studiato) associa un procedimento matematico ad hoc, spesso sproporzionato rispetto alle esigenze. Entrambi, in genere, fanno matematica decontestualizzata, depurata da intuizioni e prototipi di matematizzazione che possano aiutare l'alunno nella gestione del transfer dei concetti. Ed entrambi fanno una propria matematica, con linguaggi, procedure, forme di presentazione spesso conflittuali: la matematica dell'insegnante di matematica, la matematica dell'insegnante di economia, quella dell'insegnante di elettronica, … e quella dell'insegnante di matematica quando insegna fisica.

09   Approfondisco queste considerazioni con qualche esempio riferito alla scuola superiore.

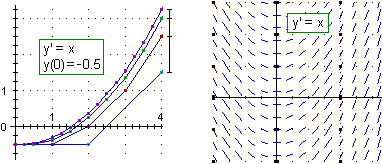
   La figura precedente, a sinistra, illustra, in un caso elementare, l'applicazione del metodo di Eulero per risolvere equazioni differenziali (che consiste nell'approssimare la soluzione con una funzione continua lineare a tratti). Con un opportuno programma è facile studiare (graficamente e/o numericamente) la convergenza della soluzione approssimata all'aumentare del numero dei sottointervalli. A destra è raffigurato il campo direzionale, anch'esso rappresentabile con un semplice programma. L'analisi del campo direzionale consente di studiare esistenza e unicità delle soluzioni, individuare le biforcazioni, … .

   Il concetto di derivata storicamente è nato, nell'ambito della matematizzazione della fisica, non a sè, ma come elemento costitutivo delle equazioni differenziali. Nel liceo scientifico è in terza, all'inizio dell'insegnamento della fisica, che si incontrano le prime equazioni differenziali, anche se non vengono individuate come tali. Poi, dopo un lungo letargo, in quinta ricompaiono (solo) le derivate, nelle ore di matematica, per studiare funzioni! Negli isituti tecnici, invece, si imparano meccanicamente un po' di formulette e procedimenti più o meno laboriosi per risolvere alcune particolari classi di equazioni differenziali.

   L'idea di modello differenziale, fondamentale nella storia e nel ruolo della matematica, rimane così oscurata. Le motivazioni? Per i licei: non c'è il tempo per studiare le equazioni differenziali. Per gli istituti tecnici: i concetti sono difficili, e le formule risolutive devono impararle per le altre materie. Occorrerebbe, invece, mettere a fuoco e delimitare il ruolo delle tecniche: che cosa è delegabile al computer (o alla consultazione di un manuale)? che cosa è essenziale per imparare a scegliere e usare criticamente le tecniche? vi sono tecniche più "trasparenti" e/o che si integrano meglio con la costruzione/comprensione dei concetti?

   Riflettere su che cosa si può fare (risoluzione di singole equazioni, sperimentazioni e congetture generali, …) con il semplice metodo di Eulero (o metodi simili) è uno dei possibili punti di partenza per sviluppare considerazioni su questi problemi. Le conclusioni potrebbero divergere da quelle della commissione dell'U.M.I. sul nuovo "syllabus", che, per combattere l'immagine della matematica come insieme di tante cose da studiare con tante tecniche, ha lanciato un messaggio del tipo: «insegnare poche "cose" di base; sarà poi l'università a innestare su queste lo studio dei "concetti" più significativi»; l'avvio ai modelli differenziali e stocastici sarebbe un lusso, in questa logica che, di fatto, trascura gran parte delle riflessioni degli ultimi decenni sui processi mentali attraverso cui si costruiscono i concetti matematici.

10   Un altro esempio. Lo studio sperimentale (con una doppia applicazione del metodo di Eulero o di un metodo simile) della equazione differenziale del 2° ordine che modellizza il comportamento di un pendolo senza (a sinistra) e con (a destra) smorzamento.

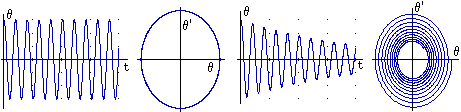
   Questi grafici, ottenuti mediante un metodo "approssimato", rappresentano le soluzioni "esatte" per casi in cui il pendolo viene rilasciato da un angolo θ di 30°; per il caso senza smorzamento, il diagramma θ-θ' consente di individuare chiaramente la periodicità. Con l'usuale metodo simbolico, basato sull'ipotesi delle piccole oscillazioni, si ottiene "esattamente" una "approssimazione" della soluzione, ma non se ne valuta la precisione, e in genere non si spiega come dalla periodicità di questa si possa dedurre quella della soluzione giusta. Non è detto che un approccio numerico sia meno rigoroso di un approccio simbolico!

   La rappresentazione grafica, e il metodo stesso di approssimazione numerica, la possibilità di vedere facilmente che cosa accade variando qualche parametro, ... (per questo e altri fenomeni, di meccanica, termodinamica, elettronica, …) mettono bene in luce la natura "concettuale" della modellizzazione matematica attraverso cui si articola la fisica classica.

   Si parla di modelli formali (o empirici) quando M viene costruito preoccupandosi solo del fatto che vi sia una analogia di comportamento tra AM e AR. Si parla di modelli concettuali quando invece i parametri EM del modello vengono scelti e messi in relazione tra loro in modo da riprodurre il modo in cui i fattori ER determinano il comportamento AR.

   Il ruolo della matematica nell'insegnamento della fisica viene invece spesso mistificato, proponendo modellizzazioni "formali" nei casi in cui sarebbe più significativo un approccio "concettuale", come quando la messa a fuoco di una legge fisica viene banalizzata alla rappresentazione grafica di qualche dato sperimentale e alla ricerca di una funzione approssimante. Può capitare di far scoprire agli alunni per questa via (con il "metodo sperimentale") la legge della dilatazione termica, mentre la temperatura è stata "definita" come grandezza in relazione lineare con la lunghezza della colonnina di mercurio!

   Il rapporto tra aspetti normativi e aspetti descrittivi (vedi 02-04) offrirebbe invece numerosi spunti didattici per uno sviluppo interattivo di concetti fisici e concetti matematici (sia di analisi che di geometria).

11   Sono modelli normativi anche quelli che regolano il funzionamento dei videogiochi: è mediante l'incorporamento di matematica che essi simulano la realtà. Si pensi più in generale alle applicazioni software (grafiche, musicali, …) e agli automatismi di tipo elettronico (che sono ormai praticamente tutti hardware+software). Scorpire come funzionano, analizzarne i limiti, … comporta un intreccio tra la messa a punto di modelli descrittivi e la scoperta dei modelli normativi. Sotto a sinsitra è riprodotto lo studio del modello differenziale di una palla che rimbalza. Le interazioni, in questi contesti, riguardano, naturalmente, anche l'informatica.

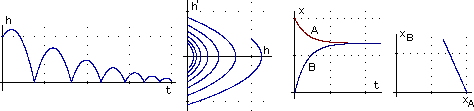
12   La parte destra della figura precedente è lo studio della modellizzazione differenziale di «A e B vanno uno incontro all'altro con velocità proporzionale alla distanza tra loro, con coefficienti di proporzionalità 1 e 2 rispettivamente». A e B si incontrano (in un punto che dista dalla posizione iniziale di A un terzo della distanza iniziale tra A e B)?

   Nel modello A e B non si incontrano, così come, nei modelli matematici, l'oggetto tolto dal frigo non raggiunge mai la temperatura ambiente, l'isotopo C-14 non sparisce dal fossile organico, … . Il confronto tra "in teoria" e "in pratica" è un altro aspetto tipico dei rapporti tra matematica e altre discipline. Ma questo esempio permette di accennare anche ad un'altra problematica: quella del ruolo svolto dalla idealizzazione matematica nell'evoluzione del pensiero scientifico e filosofico. Qui abbiamo a che fare con il problema del continuo, sia spaziale che temporale, e con quello dell'infinito.

   Quanto, l'insegnante di matematica-fisica e quello di filosofia, sfruttano le occasioni di confronto che la storia del pensiero (e la vita stessa dei filosofi-matematici-scienziati che hanno fatto questa storia) offre loro? E quale responsabilità ha l'insegnante di matematica che sfrutta l'"ignorante" Zenone, che non conosceva le serie, per motivare l'introduzione dei "potenti" strumenti dell'analisi, quando i suoi paradossi non ponevano solo problemi di convergenza (per altro alla portata della teoria geometrica delle proporzioni del pensiero greco dell'epoca), ma affrontavano problematiche gnoseologiche quali la natura dello spazio e del tempo (continua o non, archimedea o non, …)? Quanto vengono esplicitati i rapporti tra matematica e fisica, evidenziate le differenze, messo a fuoco, ad esempio, il ruolo ambiguo che la variabile tempo assume implicitamente in varie attività geometriche (la confusione tra il movimento della fisica e quello delle trasformazioni geometriche era lecita nella geometria-fisica di Euclide, non lo è più nella matematica dei nostri giorni, basata su una distinzione tra modelli e realtà)?

13   Non c'è solo la fisica. La figura seguente introduce i rapporti con il disegno.

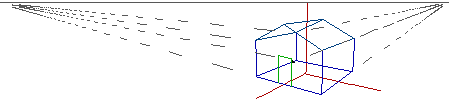
   Il problema della rappresentazione prospettica è stato un altro momento importante nell'evoluzione del pensiero matematico. E nella storia del pensiero scientifico hanno svolto un ruolo importante non solo i matematici-filosofi naturali, ma anche i matematici-artisti.

   Perchè con l'insegnamento geometrico non sviluppare una maggiore consapevolezza sulle tecniche di disegno apprese in altre materie? Perchè non sfruttare il software grafico per fare esplorazioni geometriche? Perchè non cogliere le occasioni che questo contesto offre per dare un respiro maggiore alla problematica dei concetti di limite e di infinito?

   Osserviamo la figura seguente. Si tratta di due visioni dello stesso oggetto, ottenute con un semplice programma di grafica 3D. È un ramo di iperbole nel piano x,y del sistema tracciato.

   A sinistra l'iperbole appare circolare in quanto è vista con uno sguardo orizzontale e parrallelo alla bisettrice dell'angolo x,y. L'origine degli assi diventa un punto all'infinito, gli assi x e y diventano paralleli, i punti all'infinito loro direzioni diventano gli estremi del semicerchio.

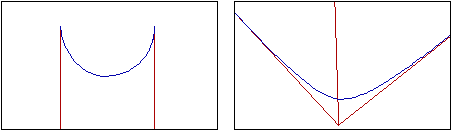
   Lo studio delle coniche in questo contesto può assumere motivazioni e operatività nuove.

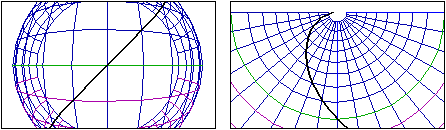
14   La cartografia, argomento "freddo" di scienze, è un'altra tematica che ha appassionato l'umanità e ha accompagnato lo sviluppo della matematica (sia della geometria che di concetti come quello di logaritmo). La problematica delle rotte, quella della interpretazione delle informazioni deducibili da una rappresentazione cartografica, l'uso di software per esplorare il globo da diversi punti di vista (sotto sono riprodotte due visioni di un emisfero con la rotta y=x, x longitudine, y latitudine), la relatività del concetto "rettilineo", l'esistenza di diversi modelli di "spazio", … offrono spunti per ricche e motivate attività didattiche.

15   L'ultimo esempio fa riferimento agli impieghi della statistica. Già in 02 e 06 abbiamo considerato modellizzazioni statistiche. La statistica, e la probabilità, possono svolgere un ruolo importante nell'educazione alla matematizzazione:

     da una parte, al livello degli studi pre-universitari, i problemi statistici non sono "interni": viene presentata una realtà (più o meno pre-modellizzata) di cui occorre costruire un modello matematico e la soluzione del problema in genere passa attraverso forme di ragionamento che intrecciano considerazioni formali e riferimenti diretti o metaforici a contesti;

     dall'altra la statistica consente attività di modellizzazione significative utilizzando concetti e tecniche matematiche relativamente elementari, facilitando la messa a fuoco della problematica della modellizzazione (natura e limiti dei rapporti tra M e R).

   L'esempio sotto raffigurato si riferisce alla rappresentazione di pesi e altezze degli studenti di un corso universitario. La nuvoletta allungata obliquamente fa supporre che vi sia un'alta correlazione tra peso e altezza; il calcolo fornisce il valore 0.78. Ma se ci si restringe alla popolazione femminile si trova il valore molto più basso 0.52 (un'ingannevole intuizione farebbe invece supporre che, restringendosi a un campione più omogeneo, la correlazione dovrebbe aumentare). La rappresentazione grafica delle sottopopolazioni maschile e femminile mette in luce come il fenomeno sia dovuto all'unione di due sottopopolazioni omogenee e con caratteristiche diverse l'una dall'altra: le due nuvolette sono più tozze della nuvola unione (e la coppia delle rette di regressione per M e F è più divaricata che per MF).

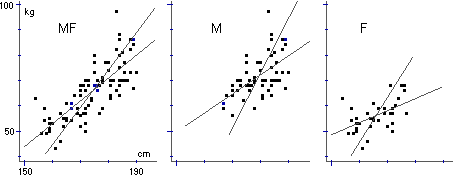
   Quest'esempio offre lo spunto per qualche ulteriore considerazione:

     l'importanza di individuare situazioni prototipo, semplici ma significative, che l'alunno possa poi richiamre mentalmente per orientarsi nelle attività di matematizzazione (come associare relazioni matematiche ad aspetti del fenomeno, tener conto dei limiti dei modelli, …);

     l'importanza e la potenza dei linguaggi grafici e delle metafore geometriche, sempre più usati nelle applicazioni ma piuttosto trascurati nell'insegnamento della matematica, mentre (vedi 09) consentirebbero in molti casi approcci ad argomenti importanti (per la cultura di base) che sono concettualmente, ma non "tecnicamente", alla portata degli alunni.

16   Concludendo, il messaggio che ho cercato di lanciare può essere così sintetizzato. L'insegnamento della matematica ha in comune con quello delle altre materie la questione della modellizzazione, sia in generale che in relazione a contesti e/o concetti specifici; su questo terreno si possono trovare forme di collaborazione che consentano di ottimizzare le attività didattiche, di motivare e dare agli alunni una visione meno scolastica delle discipline, di educarli alla gestione del transfer delle conoscenze da un contesto all'altro, da un ambito formale a un ambito applicativo e viceversa. Se non ci si sporcano le mani con i contesti, non si può comprendere la natura astratta della matematica.

 
Riferimenti

– Blum, W. & Niss, M.:1991, Applied Mathematical Problem Solving, Modelling, Applications, and Links to Other Subjects, Educational Studies in Mathematics, v. 22

– Dapueto, C. & Parenti, L.:1999, Contributions and Obstacles of Contexts in the Development of Mathematical Knowledge, Educational Studies in Mathematics [to appear]

– Israel, G.: 1996, La visione matematica della realtà, Il Mulino, Bologna

– Norman, D.A.:1995, Le cose che ci fanno intelligenti, Feltrinelli