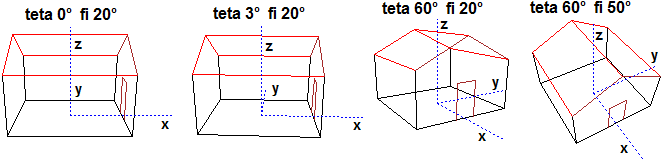
 # (see S11 too)
# If I want change the margin size I can use MARG(0.2) (reduce it to 0.2 inch) or MARG(…)
f = function(x,y) sin(x)+cos(2*y)
# I choose the size of the domain and the amount of grid lines
x = seq(-pi,pi, len=20); y = seq(-pi,pi, len=20)
# I create the "table" that x and y values associate z values
z = outer(x,y,f)
MARG(0.2); persp(x,y,z,phi=60,theta=30,d=20,col="yellow",ticktype="detailed",cex.axis=0.8,cex.lab=0.8)
# The range of z is chosen automatically. I can change it if I add in "persp" (e.g.) …,zlim=c(-4,4),… [see
# If I want no color, and reduce the distance the 2nd graph]
MARG(0.2); persp(x,y,z,phi=60,theta=30,d=2,col=NULL,ticktype="detailed",cex.axis=0.8,cex.lab=0.8)
dev.new() # If I want open a new window (to retain the last graph)
# If I want to choose the size of the window I can use BF=…; HF=…; NW() instead
# With "expand" I can apply an expansion to the z coordinates
MARG(0.2); persp(x,y,z,phi=60,theta=30,d=20,col="cyan",ticktype="detailed",expand=0.5,cex.axis=0.8,cex.lab=0.8)
# (I must introduce scale=FALSE if I want a monometric system)
# without "ticktype":
dev.new(); MARG(0.2); persp(x,y,z,phi=60,theta=30,d=20,col="green", expand=1.5,cex.axis=0.8,cex.lab=0.8)
# (see S11 too)
# If I want change the margin size I can use MARG(0.2) (reduce it to 0.2 inch) or MARG(…)
f = function(x,y) sin(x)+cos(2*y)
# I choose the size of the domain and the amount of grid lines
x = seq(-pi,pi, len=20); y = seq(-pi,pi, len=20)
# I create the "table" that x and y values associate z values
z = outer(x,y,f)
MARG(0.2); persp(x,y,z,phi=60,theta=30,d=20,col="yellow",ticktype="detailed",cex.axis=0.8,cex.lab=0.8)
# The range of z is chosen automatically. I can change it if I add in "persp" (e.g.) …,zlim=c(-4,4),… [see
# If I want no color, and reduce the distance the 2nd graph]
MARG(0.2); persp(x,y,z,phi=60,theta=30,d=2,col=NULL,ticktype="detailed",cex.axis=0.8,cex.lab=0.8)
dev.new() # If I want open a new window (to retain the last graph)
# If I want to choose the size of the window I can use BF=…; HF=…; NW() instead
# With "expand" I can apply an expansion to the z coordinates
MARG(0.2); persp(x,y,z,phi=60,theta=30,d=20,col="cyan",ticktype="detailed",expand=0.5,cex.axis=0.8,cex.lab=0.8)
# (I must introduce scale=FALSE if I want a monometric system)
# without "ticktype":
dev.new(); MARG(0.2); persp(x,y,z,phi=60,theta=30,d=20,col="green", expand=1.5,cex.axis=0.8,cex.lab=0.8)


 # The contour lines (I increase "len" to have smoother lines) of the same "f" (see):
x = seq(-pi,pi, len=200); y = seq(-pi,pi, len=200); z = outer(x,y,f)
MARG(0.4); contour(x,y,z, levels = c(-1,-0.5,0,0.5,1) ,cex.axis=0.8,cex.lab=0.8)
gridh( c(-pi/2,0,pi/2) ); gridv( c(-pi/2,0,pi/2) )
# On the right if we use nlevels=6 instead of levels=…:
# The contour lines (I increase "len" to have smoother lines) of the same "f" (see):
x = seq(-pi,pi, len=200); y = seq(-pi,pi, len=200); z = outer(x,y,f)
MARG(0.4); contour(x,y,z, levels = c(-1,-0.5,0,0.5,1) ,cex.axis=0.8,cex.lab=0.8)
gridh( c(-pi/2,0,pi/2) ); gridv( c(-pi/2,0,pi/2) )
# On the right if we use nlevels=6 instead of levels=…:
 # But the contour lines can be obtained with the standard commands (see):
PLANE(-3,3, -3,3); g = function(x,y) f(x,y)-k
k=0; CUR(g,"black"); for(k in c(-1,-0.5)) CUR(g,"red"); for(k in c(1,0.5)) CUR(g,"blue")
# But the contour lines can be obtained with the standard commands (see):
PLANE(-3,3, -3,3); g = function(x,y) f(x,y)-k
k=0; CUR(g,"black"); for(k in c(-1,-0.5)) CUR(g,"red"); for(k in c(1,0.5)) CUR(g,"blue")
 # If I want an empty box I must put in z (4 times) the base and use "zlim". See here:
x = c(-pi,pi); y = c(-pi,pi) # extremes of x and y
z0 = c(-4,4); u = rep(z0[1],4); z=array(u,dim=c(2,2)) # z0: range of 3rd dimension
BF=4; HF=4
NW(); MARG(0.2)
persp(x,y,z,phi=60,theta=30,d=20,col="yellow",ticktype="detailed",cex.axis=0.8,cex.lab=0.8,zlim=z0)
NW(); MARG(0.2)
persp(x,y,z,phi=60,theta=30,d=20,ticktype="detailed",cex.axis=0.8,cex.lab=0.8,zlim=z0)
# If I want an empty box I must put in z (4 times) the base and use "zlim". See here:
x = c(-pi,pi); y = c(-pi,pi) # extremes of x and y
z0 = c(-4,4); u = rep(z0[1],4); z=array(u,dim=c(2,2)) # z0: range of 3rd dimension
BF=4; HF=4
NW(); MARG(0.2)
persp(x,y,z,phi=60,theta=30,d=20,col="yellow",ticktype="detailed",cex.axis=0.8,cex.lab=0.8,zlim=z0)
NW(); MARG(0.2)
persp(x,y,z,phi=60,theta=30,d=20,ticktype="detailed",cex.axis=0.8,cex.lab=0.8,zlim=z0)
 #
# MINF2
#
# MINF2 #
# Another example (figure above right):
#
# Another example (figure above right):
 # See here for partial derivatives and hessian
# To go deep:
# See here for partial derivatives and hessian
# To go deep:
 F = function(x,y) { r = sqrt(x^2+y^2); ifelse(r==0, 10, 10 * sin(r)/r) }
x1 = -10; x2 = 10; y1 = -10; y2 = 10; z1=-3; z2=10
x=seq(x1,x2,len=31); y=seq(y1,y2,len=31); z = outer(x,y,F)
BF=4; HF=3
NW(); MARG(0.3)
G=persp(x,y,z,phi=30,theta=30,d=2,col="lightblue",ticktype="detailed",cex.axis=0.8,
cex.lab=0.8,expand=0.5,zlim=c(z1,z2))
xE = c(-10,10); xy = expand.grid(xE, xE)
points(trans3d(xy[,1], xy[,2], 6, pmat = G), col="red", pch =16)
lines (trans3d(x, y=10, z= 6 + sin(x), pmat = G), col="green")
f = function(x) { r = sqrt(x^2); ifelse(r==0, 10, 10*sin(r)/r) }
r1 = maxmin(f,5,10); r1
# 7.725252
t=seq(0, 2*pi, len=201); xr=r1*cos(t); yr=r1*sin(t)
lines (trans3d(xr, yr, F(xr,yr), pmat = G), col="brown",lwd=2)
# the corresponding curve levels (they are 2)
f(r1)
# 1.283746
x = seq(-10,10, len=400); y = seq(-10,10, len=400); z = outer(x,y,F)
BF=3; HF=3; NW(); MARG(0.4); contour(x,y,z, levels = 1.283, cex.axis=0.8,cex.lab=0.8)
# or:
f = function(x,y) F(x,y)-k; PLANE(-10,10, -10,10); k=1.2837; CURVE(f,"brown")
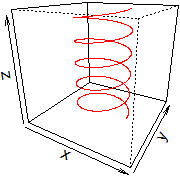
# A curve in space (5 laps of a propeller)
t = seq(0,10*pi,len=1000)
z0 = c(0,10*pi); u = rep(z0[1],4) # I put the box base in u
z = array(u,dim=c(2,2)); x = c(-2,2); y = c(-2,2)
F = persp(x,y,z,theta=30,phi=20,scale=TRUE,zlim=z0,xlim=x,ylim=y,d=1)
lines(trans3d(cos(t),sin(t),t,pmat=F),col="red")
# To have it without the box I would have added in persp: border="white",box=FALSE
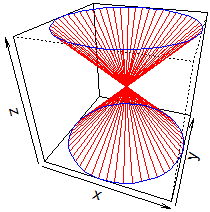
# See here how to obtatin the figure below in the center:
F = function(x,y) { r = sqrt(x^2+y^2); ifelse(r==0, 10, 10 * sin(r)/r) }
x1 = -10; x2 = 10; y1 = -10; y2 = 10; z1=-3; z2=10
x=seq(x1,x2,len=31); y=seq(y1,y2,len=31); z = outer(x,y,F)
BF=4; HF=3
NW(); MARG(0.3)
G=persp(x,y,z,phi=30,theta=30,d=2,col="lightblue",ticktype="detailed",cex.axis=0.8,
cex.lab=0.8,expand=0.5,zlim=c(z1,z2))
xE = c(-10,10); xy = expand.grid(xE, xE)
points(trans3d(xy[,1], xy[,2], 6, pmat = G), col="red", pch =16)
lines (trans3d(x, y=10, z= 6 + sin(x), pmat = G), col="green")
f = function(x) { r = sqrt(x^2); ifelse(r==0, 10, 10*sin(r)/r) }
r1 = maxmin(f,5,10); r1
# 7.725252
t=seq(0, 2*pi, len=201); xr=r1*cos(t); yr=r1*sin(t)
lines (trans3d(xr, yr, F(xr,yr), pmat = G), col="brown",lwd=2)
# the corresponding curve levels (they are 2)
f(r1)
# 1.283746
x = seq(-10,10, len=400); y = seq(-10,10, len=400); z = outer(x,y,F)
BF=3; HF=3; NW(); MARG(0.4); contour(x,y,z, levels = 1.283, cex.axis=0.8,cex.lab=0.8)
# or:
f = function(x,y) F(x,y)-k; PLANE(-10,10, -10,10); k=1.2837; CURVE(f,"brown")
# A curve in space (5 laps of a propeller)
t = seq(0,10*pi,len=1000)
z0 = c(0,10*pi); u = rep(z0[1],4) # I put the box base in u
z = array(u,dim=c(2,2)); x = c(-2,2); y = c(-2,2)
F = persp(x,y,z,theta=30,phi=20,scale=TRUE,zlim=z0,xlim=x,ylim=y,d=1)
lines(trans3d(cos(t),sin(t),t,pmat=F),col="red")
# To have it without the box I would have added in persp: border="white",box=FALSE
# See here how to obtatin the figure below in the center:
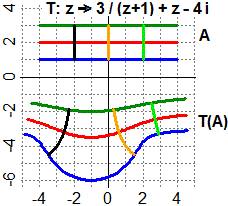 # See here for the figure on the right (a conformal map): for other references to
# complex numbers see K3
# See here for sequences, series and Fourier series.
# See also Math & Music (slides and references)
# See here for the figure on the right (a conformal map): for other references to
# complex numbers see K3
# See here for sequences, series and Fourier series.
# See also Math & Music (slides and references)
 # For figure above and the our space (which is non-Euclidean) see here and
# Walking on the balls (see "animazione" and "approfondimenti")
# The matrices (see) are table of data that can be introduced as arrays:
A = array(data=c(2,6,9), dim=c(1,3))
nrow(A); ncol(A); A; t(A)
# [1] 1
# [1] 3
# [,1] [,2] [,3] A
# [1,] 2 6 9
# [,1] t(A): the transpose of A
# [1,] 2
# [2,] 6
# [3,] 9
B = array(data=c(1,5,8),dim=c(3,1) ); B
# [,1]
# [1,] 1
# [2,] 5
# [3,] 8
C = array(data=c(1,2, 5,3, 7,8), dim=c(2,3) ); C
# [,1] [,2] [,3] the data are introduced by columns
# [1,] 1 5 7
# [2,] 2 3 8
E = array(data=c(1,2, 5,3), dim=c(2,2) ); E # I don't use D: it is used for derivatives
# [,1] [,2]
# [1,] 1 5
# [2,] 2 3
# After the name I can put the indices to identify an element:
B[3]; E[1,2]
# 8 5
A %*% B # %*% multiplies two matrices (1st row * 1st col,
# [,1] # 2nd row * 1st col, …)
# [1,] 104 # C %*% E is not defined
B %*% A # I can compute t(A)+B and t(A)-B because t(A) and
# [,1] [,2] [,3] # B have the same number of row and col
# [1,] 2 6 9
# [2,] 10 30 45
# [3,] 16 48 72
H = array(data=c(2,1,-1, 1,1,3, 0,9,2), dim=c(3,3) ); H; H %*% H %*% H # H^3
# [,1] [,2] [,3]
# [1,] 2 1 0
# [2,] 1 1 0
# [3,] -1 3 2
# [,1] [,2] [,3]
# [1,] 13 8 0
# [2,] 8 5 0
# [3,] 2 19 8
M = INV(E) # Inverse: the matrix M such that M %*% E (and E %*% M) is the
fraction( M ) # identity matrix (diagonal entries equal to 1, other to 0)
# [,1] [,2]
# [1,] -3/7 5/7
# [2,] 2/7 -1/7
fraction(E %*% M)
# [,1] [,2]
# [1,] 1 0
# [2,] 0 1
det(E) # the determinant of the matrix E (see)
# [1] -7
# An alternative method to solve linear systems. An example:
# x+3y=3 AND 4x+2y=7, that we can already solve:
S = c(1,3,3, 4,2,7); eqSystem(S)
# [1] 1.5 0.5
# I put the coefficients col by col
ma = array(data=c(1,4, 3,2),dim=c(2,2)); no = array(data(3,7),dim=c(2,1)); ma; no
# [,1] [,2]
# [1,] 1 3
# [2,] 4 2
# [,1]
# [1,] "3"
# [2,] "7"
solve(ma,no)
# [,1]
# [1,] 1.5
# [2,] 0.5
# An alternative method to calculate scalar (or dot) product. An example:
v1 = c(1,-2,2); v2 = c(-4,1,2); prods(v1,v2)
# [1] -2
v1 %*% v2; drop(v1 %*% v2) # drop the dimensions of the array
# [,1]
# [1,] -2
# [1] -2
# For the use of arrays in statistics see here.
Other examples of use
# For figure above and the our space (which is non-Euclidean) see here and
# Walking on the balls (see "animazione" and "approfondimenti")
# The matrices (see) are table of data that can be introduced as arrays:
A = array(data=c(2,6,9), dim=c(1,3))
nrow(A); ncol(A); A; t(A)
# [1] 1
# [1] 3
# [,1] [,2] [,3] A
# [1,] 2 6 9
# [,1] t(A): the transpose of A
# [1,] 2
# [2,] 6
# [3,] 9
B = array(data=c(1,5,8),dim=c(3,1) ); B
# [,1]
# [1,] 1
# [2,] 5
# [3,] 8
C = array(data=c(1,2, 5,3, 7,8), dim=c(2,3) ); C
# [,1] [,2] [,3] the data are introduced by columns
# [1,] 1 5 7
# [2,] 2 3 8
E = array(data=c(1,2, 5,3), dim=c(2,2) ); E # I don't use D: it is used for derivatives
# [,1] [,2]
# [1,] 1 5
# [2,] 2 3
# After the name I can put the indices to identify an element:
B[3]; E[1,2]
# 8 5
A %*% B # %*% multiplies two matrices (1st row * 1st col,
# [,1] # 2nd row * 1st col, …)
# [1,] 104 # C %*% E is not defined
B %*% A # I can compute t(A)+B and t(A)-B because t(A) and
# [,1] [,2] [,3] # B have the same number of row and col
# [1,] 2 6 9
# [2,] 10 30 45
# [3,] 16 48 72
H = array(data=c(2,1,-1, 1,1,3, 0,9,2), dim=c(3,3) ); H; H %*% H %*% H # H^3
# [,1] [,2] [,3]
# [1,] 2 1 0
# [2,] 1 1 0
# [3,] -1 3 2
# [,1] [,2] [,3]
# [1,] 13 8 0
# [2,] 8 5 0
# [3,] 2 19 8
M = INV(E) # Inverse: the matrix M such that M %*% E (and E %*% M) is the
fraction( M ) # identity matrix (diagonal entries equal to 1, other to 0)
# [,1] [,2]
# [1,] -3/7 5/7
# [2,] 2/7 -1/7
fraction(E %*% M)
# [,1] [,2]
# [1,] 1 0
# [2,] 0 1
det(E) # the determinant of the matrix E (see)
# [1] -7
# An alternative method to solve linear systems. An example:
# x+3y=3 AND 4x+2y=7, that we can already solve:
S = c(1,3,3, 4,2,7); eqSystem(S)
# [1] 1.5 0.5
# I put the coefficients col by col
ma = array(data=c(1,4, 3,2),dim=c(2,2)); no = array(data(3,7),dim=c(2,1)); ma; no
# [,1] [,2]
# [1,] 1 3
# [2,] 4 2
# [,1]
# [1,] "3"
# [2,] "7"
solve(ma,no)
# [,1]
# [1,] 1.5
# [2,] 0.5
# An alternative method to calculate scalar (or dot) product. An example:
v1 = c(1,-2,2); v2 = c(-4,1,2); prods(v1,v2)
# [1] -2
v1 %*% v2; drop(v1 %*% v2) # drop the dimensions of the array
# [,1]
# [1,] -2
# [1] -2
# For the use of arrays in statistics see here.
Other examples of use