---------- ---------- ---------- ---------- ---------- ---------- ---------- ----------
# We have seen (here) that "^" calculates x^(1/3) only when x >= 0
# We can use this function (POT) to compute "^" in this case:
POT=function(a,m,n) ifelse(a>=0,a^(m/n),ifelse(m>0 & n%%2==0,1/0,ifelse(m%%2!=0,-((-a)^m)^(1/n),((-a)^m)^(1/n))))
# Example:
(-27)^(1/3)
# Not a Number
rad3(-27)
# -3
POT(-27,1,3)
# -3
POT(-27,-1,3)
# -0.3333333
(-100)^(1/7)
# Not a Number
POT(-100,1,7)
# -1.930698
#
# The correct graph of x -> x^x:
BF=3; HF=2.5
f = function(x) ifelse(x>=0, x^x, 1/0)
Plane(-2,2, -2,f(2) )
graph(f, 0,2, "brown")
# I choose m/n between 0 and 2 (m between 1 and 2n)
for(n in 1:200) for(m in 1:(2*n)) Dot(-m/n,POT(-m/n,-m,n), "seagreen")
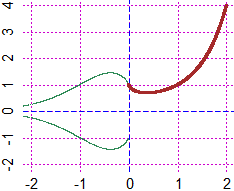 # The graph of continuos function (brown) and the other part of the graph (green).
# The green part is formed by two sets A and B of points. A are points above the
# x axis, B are points below. The two sets are "dense" but not "continuous".
Other examples of use
# The graph of continuos function (brown) and the other part of the graph (green).
# The green part is formed by two sets A and B of points. A are points above the
# x axis, B are points below. The two sets are "dense" but not "continuous".
Other examples of use
 # The graph of continuos function (brown) and the other part of the graph (green).
# The green part is formed by two sets A and B of points. A are points above the
# x axis, B are points below. The two sets are "dense" but not "continuous".
Other examples of use
# The graph of continuos function (brown) and the other part of the graph (green).
# The green part is formed by two sets A and B of points. A are points above the
# x axis, B are points below. The two sets are "dense" but not "continuous".
Other examples of use