Soffermiamoci sui quesiti proposti la volta scorsa. Non so, in dettaglio, che cosa avete proposto voi
(non ho avuto il tempo di esaminare i vostri scritti); vediamo come avrei risposto io e discutiamo alcuni problemi
che emergono (suggeriti da cose
da voi proposte durante la lezione in cui avete affrontato i quesiti). Sulle vostre risposte ci soffermeremo
la volta prossima (così come sull'altro quesito proposto). Per mia comodità espositiva, affronteremo le soluzioni con R.
(A) Quale/quali, tra tutti i triangoli di eguale superficie aventi in comune un lato, ha/hanno
perimetro minimo?
# (A) Copia via via da un gruppo di righe
# con solo # al gruppo successivo
#
dev.new(width=3.5, height=3.5, xpos=400,ypos=1)
par( mai = c(0,0,0,0) )
# Ho posizionato e dimensionato opportunamente la finestra
# (comandi non essenziali). Con fg="white" non traccio il
# box; con asp=1 faccio sist. monom.
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
abline(h=c(0,5,10,15),v=c(0,5,10,15),col="grey70",lty=2)
text(8,16.5,"Quando è massimo il perimetro?")
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H),col="red"); text(-0.5,3.5,"H")
polygon(c(0,10,5),c(0,0,H),lty=3)
polygon(c(0,10,8),c(0,0,H),border="blue",lty=3)
polygon(c(0,10,11),c(0,0,H),border="green4",lty=3)
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
text(4,-0.5,"L"); text(7,3.5,"L1"); text(12.5,3.5,"L2")
text(8,15.5,"L'esito non dipende da H")
# Dai grafici si deduce subito che l'esito non dipende da H
# (scalando verticalmente la situazione non cambia in quanto
# le lunghezze di L1 ed L2 variano proporzionlamente).
#
#
# Proviamo a fare qualche congettura (facile, col computer ...):
# Diamo via via il vertice e calcoliamo con il teorema di
# Pitagora L1+L2
# (fai via via dei clic; quando vuoi finire premi ESC)
avvio <- 0; par( mai = c(0,0,0,0) )
while(1==1) {plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
abline(h=c(0,5,10,15),v=c(0,5,10,15),col="grey50",lty=2)
lines(c(0,10),c(0,0),col="red")
text(0,-1/2,"0"); text(10,-1/2,"10")
xp <- locator(1)$x; polygon(c(0,10,xp),c(0,0,H),border="blue")
xx <- round((10+sqrt(xp^2+H^2)+sqrt((xp-10)^2+H^2))*1e4)/1e4
if (avvio > 0) text(1,15.5,paste("ex:",yp),adj=0)
yp <- xx; text(1,13.5,xx,adj=0)
avvio <- 1; locator(1) }
# differenza vicino all'asse del lato di base e' piccola (impercettibile
# senza computer); non e' facile convincersi del tutto ...
 #
# Se abbiamo conoscenze di analisi matematica basta che studiamo
# la derivata prima di sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H)); text(-0.5,4,"8")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(0,14),c(9,9)); text(5,-0.5,"10"); text(7,9.5,"x")
#
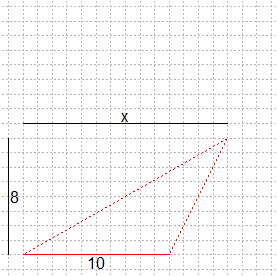
# Se abbiamo conoscenze di analisi matematica basta che studiamo
# la derivata prima di sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H)); text(-0.5,4,"8")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(0,14),c(9,9)); text(5,-0.5,"10"); text(7,9.5,"x")
 # E' facile fare il calcolo a mano. Vediamo, per curiosità, come
# farlo con R:
D(expression(sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)),"x")
0.5*(2*x*(x^2+8^2)^-0.5)+0.5*(2*(x-10)*((x-10)^2+8^2)^-0.5)
#
# Otteniamo un risultato non semplificato. Lo possiamo semplificare
# a mano, oppure lo copiamo e incolliamo in: http://www.wolframalpha.com
# (potremmo copiare anche il termine da derivare)
# Che lo semplichiamo o no troviamo (a mano, con R o usando il sito
# di cui sopra) che 5 è il punto in cui la derivata si annulla.
#
#
# Vediamo come si poteva fare più "semplicemenete":
# Costruiamo L2' ribaltando L2 rispetto alla retta che dista
# H dalla base
dev.new(width=3.5, height=3.5, xpos=400,ypos=1)
par( mai = c(0,0,0,0) )
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
abline(h=c(0,5,10,15),v=c(0,5,10,15),col="grey70",lty=2)
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H),col="red"); text(-0.5,3.5,"H")
polygon(c(0,10,5),c(0,0,H),lty=3)
polygon(c(0,10,8),c(0,0,H),border="blue",lty=3)
polygon(c(0,10,11),c(0,0,H),border="green4",lty=3)
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
text(4,-0.5,"L"); text(7,3.5,"L1"); text(12.5,3.5,"L2")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(5,10,14),c(8,H*2,H),lty=2); text(12.5,12.5,"L2'")
# L1+L2 = L1+L2' è minimo quando L1 e L2' sono allineati
# ossia quando il triangolo è isoscele.
# Questa è una semplice dimostrazione, facile da capire,
# ma non facile da ideare (come gran parte delle dimostrazioni
# di geometria "classica")
# E' facile fare il calcolo a mano. Vediamo, per curiosità, come
# farlo con R:
D(expression(sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)),"x")
0.5*(2*x*(x^2+8^2)^-0.5)+0.5*(2*(x-10)*((x-10)^2+8^2)^-0.5)
#
# Otteniamo un risultato non semplificato. Lo possiamo semplificare
# a mano, oppure lo copiamo e incolliamo in: http://www.wolframalpha.com
# (potremmo copiare anche il termine da derivare)
# Che lo semplichiamo o no troviamo (a mano, con R o usando il sito
# di cui sopra) che 5 è il punto in cui la derivata si annulla.
#
#
# Vediamo come si poteva fare più "semplicemenete":
# Costruiamo L2' ribaltando L2 rispetto alla retta che dista
# H dalla base
dev.new(width=3.5, height=3.5, xpos=400,ypos=1)
par( mai = c(0,0,0,0) )
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
abline(h=c(0,5,10,15),v=c(0,5,10,15),col="grey70",lty=2)
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H),col="red"); text(-0.5,3.5,"H")
polygon(c(0,10,5),c(0,0,H),lty=3)
polygon(c(0,10,8),c(0,0,H),border="blue",lty=3)
polygon(c(0,10,11),c(0,0,H),border="green4",lty=3)
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
text(4,-0.5,"L"); text(7,3.5,"L1"); text(12.5,3.5,"L2")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(5,10,14),c(8,H*2,H),lty=2); text(12.5,12.5,"L2'")
# L1+L2 = L1+L2' è minimo quando L1 e L2' sono allineati
# ossia quando il triangolo è isoscele.
# Questa è una semplice dimostrazione, facile da capire,
# ma non facile da ideare (come gran parte delle dimostrazioni
# di geometria "classica")
 #
# Oltre al triangolo così trovato c'è ovviamente quello
# ad esso simmetrico rispetto al lato L
#
# Oltre al triangolo così trovato c'è ovviamente quello
# ad esso simmetrico rispetto al lato L
(B) Quale/quali, tra tutti i triangoli di eguale perimetro aventi in comune un lato, ha/hanno
superficie massima?
# (B)
# Era già noto ad Euclide che il raggio di luce che arriva in uno
# specchio e quello riflesso formano con lo specchio angoli eguali;
# sappiamo anche (per il Principio di Fermat - vedi) che questo è il
# percorso più breve.
#
# Faccio un disegno per capirci (traccio anche
# l'ellisse con fuochi in (-2,0) e (2,0) )
par( mai = c(0,0,0,0) )
x1 <- -3.5; y1 <- -3; x2 <- 3.5; y2 <- 4
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="",asp=1)
abline(v=seq(-3,3,1),h=seq(y1,y2,1),lty=3)
abline(v=0,h=0); abline(h=20/12,col="brown")
n <- 80; dx <- (x2-x1)/n; dy <- (y2-y1)/n; I <- 0:n; J <- 0:n
for(i in I) for(j in J) {x <- x1+dx*i;y <- y1+dy*j;
if (abs(sqrt((x-2)^2+y^2)+sqrt((x+2)^2+y^2)-6)<0.05) points(x,y,pch=".",cex=2,col="red")}
polygon(c(-2,0,2),c(0,sqrt(5),0)); polygon(c(-2,2,2),c(0,20/12,0))
text(-2,-1/2,"A"); text(2,-1/2,"B"); text(-0.3,2.7,"H")
lines(c(-2,0,2),c(0,20/12,0),lty=3); text(-0.3,1.5,"K")
text(2.2,2.1,"Q")
 # Per il p. di F. la spezzata AKB ha lunghezza minore della spezzata
# AQB, mentre i triangoli AKB e AQB hanno la stessa area.
# Quindi AHB ha sicuramente area maggiore
# Per il p. di F. la spezzata AKB ha lunghezza minore della spezzata
# AQB, mentre i triangoli AKB e AQB hanno la stessa area.
# Quindi AHB ha sicuramente area maggiore
A questo punto, prima di continuare a riflettere su questi quesiti e sulle
vostre risposte, rivediamo qualcosa sulle coniche,
tema che è emerso affrontando (B), e incominiciamo a pensare all'importanza e al ruolo che
potevano avere e a quello che potrebbero/dovrebbero avere oggi nell'insegnamento (come affronteremmo, oggi, questi
problemi, con quali tecniche, con quali rapporti con le altre discipline, con quali differenze tra tipi
di scuole, con quale ruolo delle nuove tecnologie, …).
È un problema sollevato da
uno dei due gruppi (non dobbiamo trovare/concordare delle risposte a queste domande, ma, se poi
andremo ad insegnare, dovremo porcele).
 #
# Se abbiamo conoscenze di analisi matematica basta che studiamo
# la derivata prima di sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H)); text(-0.5,4,"8")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(0,14),c(9,9)); text(5,-0.5,"10"); text(7,9.5,"x")
#
# Se abbiamo conoscenze di analisi matematica basta che studiamo
# la derivata prima di sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H)); text(-0.5,4,"8")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(0,14),c(9,9)); text(5,-0.5,"10"); text(7,9.5,"x")
 # E' facile fare il calcolo a mano. Vediamo, per curiosità, come
# farlo con R:
D(expression(sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)),"x")
0.5*(2*x*(x^2+8^2)^-0.5)+0.5*(2*(x-10)*((x-10)^2+8^2)^-0.5)
#
# Otteniamo un risultato non semplificato. Lo possiamo semplificare
# a mano, oppure lo copiamo e incolliamo in: http://www.wolframalpha.com
# (potremmo copiare anche il termine da derivare)
# Che lo semplichiamo o no troviamo (a mano, con R o usando il sito
# di cui sopra) che 5 è il punto in cui la derivata si annulla.
#
#
# Vediamo come si poteva fare più "semplicemenete":
# Costruiamo L2' ribaltando L2 rispetto alla retta che dista
# H dalla base
dev.new(width=3.5, height=3.5, xpos=400,ypos=1)
par( mai = c(0,0,0,0) )
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
abline(h=c(0,5,10,15),v=c(0,5,10,15),col="grey70",lty=2)
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H),col="red"); text(-0.5,3.5,"H")
polygon(c(0,10,5),c(0,0,H),lty=3)
polygon(c(0,10,8),c(0,0,H),border="blue",lty=3)
polygon(c(0,10,11),c(0,0,H),border="green4",lty=3)
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
text(4,-0.5,"L"); text(7,3.5,"L1"); text(12.5,3.5,"L2")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(5,10,14),c(8,H*2,H),lty=2); text(12.5,12.5,"L2'")
# L1+L2 = L1+L2' è minimo quando L1 e L2' sono allineati
# ossia quando il triangolo è isoscele.
# Questa è una semplice dimostrazione, facile da capire,
# ma non facile da ideare (come gran parte delle dimostrazioni
# di geometria "classica")
# E' facile fare il calcolo a mano. Vediamo, per curiosità, come
# farlo con R:
D(expression(sqrt(x^2+8^2)+sqrt((x-10)^2+8^2)),"x")
0.5*(2*x*(x^2+8^2)^-0.5)+0.5*(2*(x-10)*((x-10)^2+8^2)^-0.5)
#
# Otteniamo un risultato non semplificato. Lo possiamo semplificare
# a mano, oppure lo copiamo e incolliamo in: http://www.wolframalpha.com
# (potremmo copiare anche il termine da derivare)
# Che lo semplichiamo o no troviamo (a mano, con R o usando il sito
# di cui sopra) che 5 è il punto in cui la derivata si annulla.
#
#
# Vediamo come si poteva fare più "semplicemenete":
# Costruiamo L2' ribaltando L2 rispetto alla retta che dista
# H dalla base
dev.new(width=3.5, height=3.5, xpos=400,ypos=1)
par( mai = c(0,0,0,0) )
plot(c(-1,17),c(-1,17),type="n",fg="white",asp=1)
x <- seq(-1,17,1); abline(h=x,v=x,lty=3,col="grey")
abline(h=c(0,5,10,15),v=c(0,5,10,15),col="grey70",lty=2)
H <- 8; lines(c(0,10),c(0,0),col="red")
lines(c(-1,-1),c(0,H),col="red"); text(-0.5,3.5,"H")
polygon(c(0,10,5),c(0,0,H),lty=3)
polygon(c(0,10,8),c(0,0,H),border="blue",lty=3)
polygon(c(0,10,11),c(0,0,H),border="green4",lty=3)
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
text(4,-0.5,"L"); text(7,3.5,"L1"); text(12.5,3.5,"L2")
polygon(c(0,10,14),c(0,0,H),border="red",lty=3)
lines(c(5,10,14),c(8,H*2,H),lty=2); text(12.5,12.5,"L2'")
# L1+L2 = L1+L2' è minimo quando L1 e L2' sono allineati
# ossia quando il triangolo è isoscele.
# Questa è una semplice dimostrazione, facile da capire,
# ma non facile da ideare (come gran parte delle dimostrazioni
# di geometria "classica")
 #
# Oltre al triangolo così trovato c'è ovviamente quello
# ad esso simmetrico rispetto al lato L
#
# Oltre al triangolo così trovato c'è ovviamente quello
# ad esso simmetrico rispetto al lato L
 # Per il p. di F. la spezzata AKB ha lunghezza minore della spezzata
# AQB, mentre i triangoli AKB e AQB hanno la stessa area.
# Quindi AHB ha sicuramente area maggiore
# Per il p. di F. la spezzata AKB ha lunghezza minore della spezzata
# AQB, mentre i triangoli AKB e AQB hanno la stessa area.
# Quindi AHB ha sicuramente area maggiore