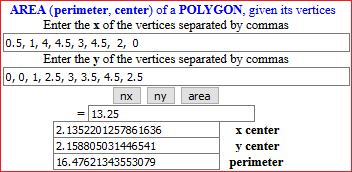
The centroid, also known as geometric center or center of plane figure F, is the center of mass (or barycenter) of a lamina of constant thickness and of a single material having the shape of F. In other words, it is the point at which a cutout of the shape F (with uniformly distributed mass) could be perfectly balanced on the tip of a pin.

•  example:

The graph with this script

 		 

The figure can be traced easily with drawing(3) or drawing(4): see.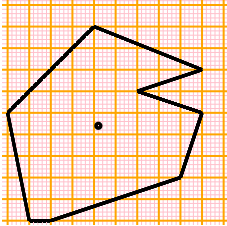

,&5&a &5&1 v&30&a&10&bw v&5&a&15&bw v&15&c&5&bw v&15&a&5&bw v&25&c&10&bw &20&7 v&5&a&25&dw
,&21&a&22&b @

Con WolframAlpha:

polygon (0.5,0),(1,0),(4,1),(4.5,2.5),(3,3),(4.5,3.5),(2,4.5),(0,2.5)

     

Graph with PHP.

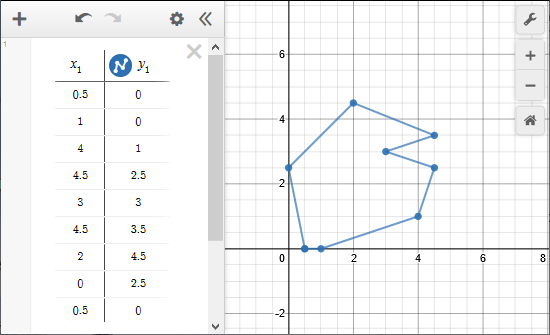
With desmos:

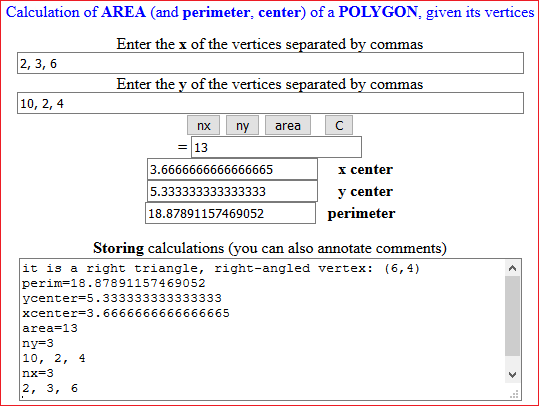
•  If the polygon is a triangle you can study it with other scripts. This script warns, however, if the triangle is rectangle:

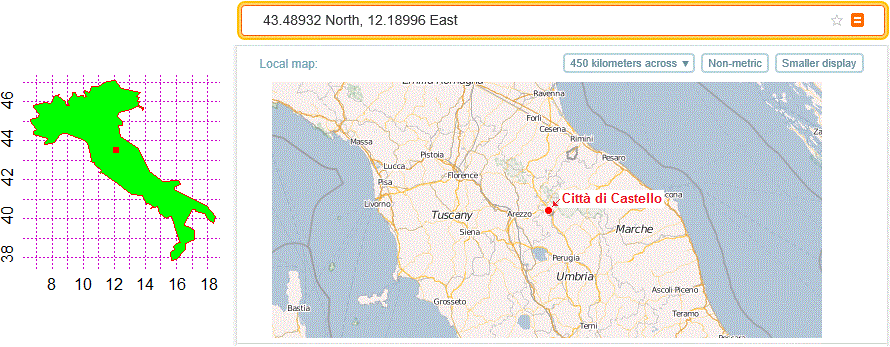
•  Il centro della penisola italiana

Enter the x of the vertices separated by commas
8,7.87,7.6,7,6.81,6.81,7.2,7.08,6.6,6.6,7,6.82,6.82,7.7,7.7,7.5,7.5,8,8.15,8.47,8.7,8.8,8.9,10.1,10.25,10.45,10.5,10.46,10.75,10.73,
11.2,11.05,11.1,11.2,12.2,13.1,13.8,14.1,14.2,14.4,14.5,14.35,14.75,14.9,15.35,15.55,15.65,16.15,16.2,16.23,16,15.83,15.9,15.6,
15.65,16,16.6,16.58,17,17.1,17.18,17.125,16.8,16.52,16.5,17,17.2,17.2,17.82,18,18.36,18.5,17.9,15.9,15.87,16.25,16.2,16.1,15.1,
15,14.23,13.55,12.4,12.28,12.5,12.5,12.2,12.3,13.1,13.5,13.8,13.8,13.9,13.85,13.6,13.55,13.6,13.5,13.6,13.4,13.65,12.45,12.1,11.5,
11,10.5,10.4,10.1,10.05,10.2,10.05,10,9.6,9.5,9.3,9.3,9,9.1,8.95,8.85,8.4,8.45,8.1,8

Enter the y of the vertices separated by commas
46,45.9,45.95,45.85,45.81,45.7,45.35,45.2,45.1,45,44.6,44.5,44.35,44.12,44.08,43.9,43.8,43.87,43.9,44.3,44.38,44.4,44.38,44,43.84,
43.3,43,42.92,42.88,42.8,42.5,42.4,42.35,42.38,41.8,41.25,41.175,40.75,40.8,40.7,40.65,40.55,40.65,40.3,40,40.1,40.1,39,38.91,38.8,
38.72,38.6,38.45,38.25,37.85,37.9,38.45,38.75,38.91,38.89,38.95,39.4,39.6,39.65,39.77,40.5,40.5,40.4,40.28,40,39.75,40.1,40.7,41.5,
41.6,41.75,41.9,41.96,41.94,42,42.45,43.63,44.2,44.78,44.8,45,45.25,45.43,45.6,45.75,45.65,45.55,45.6,45.7,45.8,45.83,46,46,46.2,
46.3,46.5,46.68,47.1,47.05,46.78,46.81,46.5,46.6,46.45,46.28,46.2,46.35,46.3,46.5,46.5,46.35,46,45.8,45.8,46,46.25,46.4,46.28,46
x center 12.189955285700773
y center 43.48931809855869

•  I connect the opposite midpoints on the sides of a convex (i.e. with all angles less than 180°) quadrilateral to form line segments. These line segments formed 4 quadrilaterals within the original quadrilateral. Is the sum of the areas of the non-adjacent quadrilateral equal to the sum of the remaining quadrilaterals?

     A + B = C + D ?

I try with the four vertices  P1 = (0,0), P2 = (6,1), P3 = (8,5), P4 = (2,6)  (see the picture).
The midponts are  M1 = (6/2,1/2) = (3,0.5), M2 = (6+(8-6)/2,1+(5-1)/2) = (7,3), M3 = (8+(2-8)/2,5+(6-5)/2) = (5,5.5), M4 = (2/2,6/2) = (1,3).
I find the intersection of M1-M3 and M2-M4 with line-line: 

   D               B               C               A   
 Enter x         Enter x         Enter x         Enter x
4, 1, 0, 3      4, 7, 6, 3      4, 5, 8, 7      4, 5, 2, 1
 Enter y         Enter y         Enter y         Enter y
3, 3, 0, 0.5    3, 3, 1, 0.5    3, 5.5, 5, 3    3, 5.5, 6, 3
area = 8        area = 6.5      area = 7        area = 8.5

D + C = 8 + 7 = 15;  A + B = 8.5 + 6.5 = 15.  OK

I also try with (0,4), (5,0), (13,10), (6,11).
Midpoints: (2.5,2), (9,5), (9.5,10.5), (3,7.5). Intersection of M1-M3 and M2-M4: 		    

            x                 y
D     6, 3, 0, 2.5     6.25, 7.5, 4, 2       area = 15.9375
B     6, 2.5, 5, 9     6.25, 2, 0, 5         area = 18.8125
C     6, 9, 13, 9.5    6.25, 5, 10, 10.5     area = 18.3125
A     6, 9.5, 6, 3     6.25, 10.5, 11, 7.5   area = 15.4375

D + C = 15.9375 + 18.3125 = 34.25;  A + B = 15.4375 + 18.8125 = 34.25.  OK