Distance between ellipses with horizontal and vertical axes  (here)

Example.

The distance between  x=cos(t)+1, y=1.5*sin(t)+2  and  x=2*cos(t)+5, y=sin(t)+4

With N=6 and CLICK. The algorithm takes 2*10^7 points of the two ellipses at random. If I repeat I get slightly different values.

d = 1.5157354877226683 1.515735 (20*10^6 trials) P1=(1.7598987886578747,2.975062110709704) P2=(3.076393276713425,3.726258710583019) (1.759899,2.975062) (3.076393,3.726259)

If I want more precise values, click+. I do 2*10^8 more trials.

d = 1.515735320276885 1.515735 (220*10^6 trials) P1=(1.7598615664468806,2.975127376106839) P2=(3.076755995043274,3.725622296187349) (1.759862,2.975127) (3.076756,3.725622)

If I want more precise values, click++. I do 2*10^9 more trials (I put N=8).

d = 1.515735233339863 1.51573523 (2220*10^6 trials) P1=(1.759903834272297,2.9750532631508335) P2=(3.0766332895032336,3.7258374127671465) (1.75990383,2.97505326) (3.07663329,3.72583741)

I stop, I can take 1.5157352±0.0000001
Similarly the closest points are (1.7599±0.0001,2.9750±0.0001) and (3.0766±0.0001,3.7258±0.0001)

The ellipses (and the distance) with Desmos:

The ellipses with WolfranAlpha:

Another example:

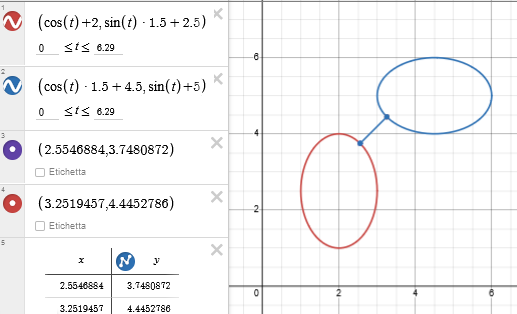
d = 0.9860241507797305  0.986024    (4220*10^6 trials)
P1=(2.5546884044301406,3.748087233120817) P2=(3.251945737231238,4.445278625620745)
(2.554688,3.748087)  (3.251946,4.445279)
d = 0.9860241662756983  0.986024    (2220*10^6 trials)
P1=(2.554590454246272,3.748185167806666) P2=(3.2518782140464175,4.445346151018277)
(2.55459,3.748185)  (3.251878,4.445346)
d = 0.9860242035531152  0.986024    (220*10^6 trials)
P1=(2.5548853798442934,3.7478902132314653) P2=(3.2520786639100256,4.445145729270022)
(2.554885,3.74789)  (3.252079,4.445146)
d = 0.986026008078451  0.986026    (20*10^6 trials)
P1=(2.555703244079048,3.747071082645272) P2=(3.252931565336402,4.444294114855036)
(2.555703,3.747071)  (3.252932,4.444294)

If one ellipse is a point ... The distance from (10, 10) and the curve x=2*cos(t)+2, y=5*sin(t)-1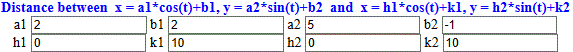

distance = 9.64470018696     nearest point of the curve = (2.8155786, 3.5653802)

d = 9.644700186960899  9.6447001870    (2220*10^6 trials)
P1=(2.8155786459581336,3.5653802362570923) P2=(10,10)
(2.8155786460,3.5653802363)  (10,10)
d = 9.644700186960899  9.6447001870    (220*10^6 trials)
P1=(2.8155786459581336,3.5653802362570923) P2=(10,10)
(2.8155786460,3.5653802363)  (10,10)
d = 9.644700186960902  9.6447001870    (20*10^6 trials)
P1=(2.815578570087272,3.56538032096889) P2=(10,10)
(2.8155785701,3.5653803210)  (10,10)