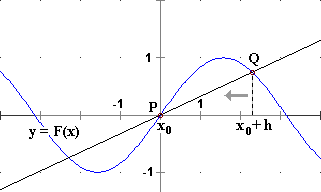
The derivative of F at x0
 The derivative of F at x0 |
 |
Alternatively, I can use pocket calculator
•• At the beginning the function x → x³+1 is calculated.
function F(x) {
with(Math) {
return pow(x,3)+1
}}

For x1 = 4, x2 = 4.00000001 I have 48: the derivative of x → x³+1 in 4.
To change F open the Code and modify F(x)
Save by clicking here (with the right mouse button) the file on your computer
(change the name if you want, but leave ".htm").
At this point you can use it to study any function.
Just open the source code, edit F(x), and run "save".
You can repeat this several times.
•• If I want the derivative in 0 of:
function F(x) {
with(Math) {
if (x==0) {y = -1} else {y = (x*x+x)/(x*(abs(x)-1)) }
return y
}}

in 0, "from the left" the derivative in 0, "from the right" it is −2:

function F(x) {
with(Math) {
y = cos(x)/(2*pow(x,2)+3)
return y
}}

x1 = 2.999999999, x2 = 3.000000001 -> DF/Dx = 0.020218571670441426 x1 = 2.99999999, x2 = 3.00000001 -> DF/Dx = 0.020218571037598457 x1 = 2.9999999, x2 = 3.0000001 -> DF/Dx = 0.020218570947809964 x1 = 2.999999, x2 = 3.000001 -> DF/Dx = 0.020218570953527932 x1 = 2.99999, x2 = 3.00001 -> DF/Dx = 0.020218570951017416 x1 = 2.9999, x2 = 3.0001 -> DF/Dx = 0.020218570849868743 x1 = 2.999, x2 = 3.001 -> DF/Dx = 0.020218560713802937 x1 = 2.99, x2 = 3.01 -> DF/Dx = 0.02021754710226442 x = 3 -> F(x) = -0.04714249983811645
I understand that, from a certain point on, rounding errors become predominant.
I can round the derivative in 3 with 0.02021857095. If I did the calculation of the derivative formally I would get
•• If I want the derivative in 2 of:
function F(x) {
with(Math) {
y = sqrt(x+sqrt(x+sqrt(x)))
return y
}}
x1 = 1.999999999, x2 = 2.000000001 -> DF/Dx = 0.3482589483968381 x1 = 1.99999999, x2 = 2.00000001 -> DF/Dx = 0.34825893491952525 x1 = 1.9999999, x2 = 2.0000001 -> DF/Dx = 0.34825892410451564 x1 = 1.999999, x2 = 2.000001 -> DF/Dx = 0.3482589245773269 x1 = 1.99999, x2 = 2.00001 -> DF/Dx = 0.3482589246294687 x1 = 1.9999, x2 = 2.0001 -> DF/Dx = 0.3482589247335425 x1 = 1.999, x2 = 2.001 -> DF/Dx = 0.3482589354979854 x1 = 1.99, x2 = 2.01 -> DF/Dx = 0.3482600119583381 x = 2 -> F(x) = 1.9615705608064609
I understand that, from a certain point on, rounding errors become predominant. I can round the derivative in 2 with 0.3482589246. If I did the calculation of the derivative formally I would get (rounding) 0.34825892462483 (but for practical purposes 0.348259 is more than enough).
•• If I want the derivative in π/2 of:
function F(x) {
with(Math) {
y = sin(x)*sin(x)/sin(x*x)
return y
}}
x1 = 1.5707963267948966, x2 = 1.57079632679 -> DF/Dx = 6.297569381461999 x1 = 1.5707963267948966, x2 = 1.5707963267 -> DF/Dx = 6.297662947849201 x1 = 1.5707963267948966, x2 = 1.570796326 -> DF/Dx = 6.29766367514587 x1 = 1.5707963267948966, x2 = 1.57079632 -> DF/Dx = 6.297662721957301 x1 = 1.5707963267948966, x2 = 1.5707963 -> DF/Dx = 6.297662147590565 x1 = 1.5707963267948966, x2 = 1.570796 -> DF/Dx = 6.297652236263873 x1 = 1.5707963267948966, x2 = 1.57079 -> DF/Dx = 6.297453845904398 x1 = 1.5707963267948966, x2 = 1.5707 -> DF/Dx = 6.294479377944526 x1 = 1.5707963267948966, x2 = 1.57 -> DF/Dx = 6.271434713300255 x = 1.5707963267948966 -> F(x) = 1.6018813708668798
I understand that, from a certain point on, rounding errors become predominant. I can round the derivative in π/2 with 6.2976623. If I did the calculation of the derivative formally I would get (rounding) 6.2976630437795 (but for practical purposes 6.2977 is more than enough).
We can draw the graphs with JavaScript; for example, see sinsinsin (see the code; se also here).
Graphs can be plotted also with R or Desmos.