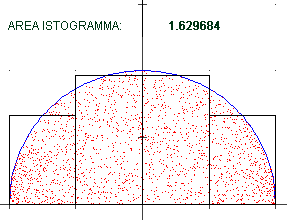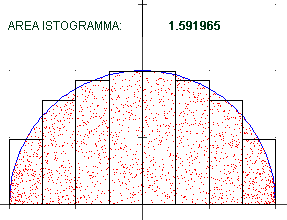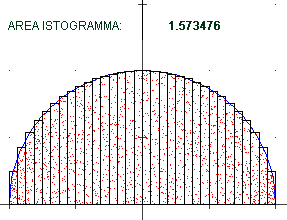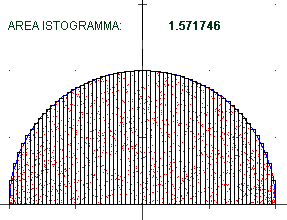
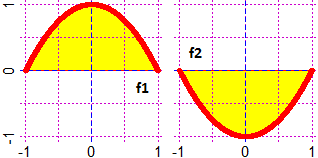
#  The integral of F (positive function) from A to B is the area below the graph and above the x axis. It is calculated by approximating it with rectangles in increasing numbers. On the right, the approximation of integral of x → √(1−x²) from −1 to 1 (1.570796… = π/2). #  I F is not always positive, then the areas of rectangles are signed: positive/negative if they are above/below the x axis: in the case shown below on the left, the integral between -1 and 1 of f1 is > 0, that of f2 is < 0. #  In the case shown below on the right, the integral between -2 and 2 is 0.

This script allows to calculate the integral of a polynomial function, eventually raised to a real exponent.

•  The oriented area above left, where f1(x) = −x²+1:

I take 1.333… = 1+1/3 = 4/3.

•  Rivediamo il caso del semicerchio:

1.5707968138960287 n = 1e4 1.5707963876831614 n = 4e4 1.5707963344059523 n = 16e4 1.5707963277462433 n = 64e4 1.570796326913793 n = 256e4

    Fermandomi qui posso prendere l'approssimazione 1.570796327 (e so che π/2 = 1.570796326794896…).

•  ∫_{[−3, 5]} 5 + 2·x − 3·x² dx

I take  −96.

We can draw the graphs with JavaScript; for example, see fun00_integ.

The graph with Desmos: