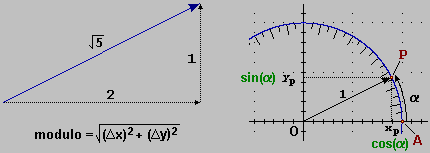
xP = 2/ 5 = 0.8944…
5 = 0.8944…
yP = 1/ 5 = 0.4472…
5 = 0.4472…
α = 0.46364…
= 26.565…°
tan(α) = pendenza
= yP/xP
Per caratterizzare i vettori di eguale direzione (ossia tali da essere uno il prodotto dell'altro per un numero positivo) posso prendere come loro rappresentante quello, tra di essi, che ha modulo uguale a 1. Sotto è raffigurato il vettore (2,1) e, a destra, applicato all'origine, il vettore di modulo 1 di eguale direzione.
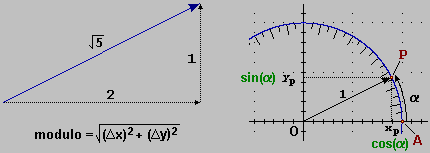 |
xP = 2/
α = 0.46364…
tan(α) = pendenza |
Per ottenere un vettore di modulo 1 diretto come un vettore dato v – come si è fatto nella figura di sopra per ottenere un vettore di intensità diretto come (2,1) – basta dividere le componenti di v per il modulo di v.
I vettori di modulo 1, poiché sono usati per rappresentare le direzioni verso cui possono essere diretti i vettori, vengono detti versori, oltre che vettori unitari. Se rappresento i versori applicati all'origine O = (0,0), le loro "punte" cadono sul cerchio di centro O e raggio 1. Nella figura precedente OP è il versore del vettore (2,1).
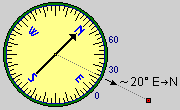
Invece che con i versori, le direzioni possono essere identificate con numeri, come accade quando si usa una bussola.
scelgo un punto cardinale (ad es. E) e un verso (ad es. quello antiorario) e trovo di quanti gradi approssimativamente devo ruotare da E nel verso scelto per puntare sulla località. Nel caso illustrato la località è nella direzione 20° E-N (circa).
|
 |
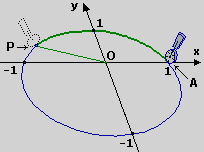
Per determinare le direzioni con la precisione che voglio, senza limitazioni, devo trovare una nuova tecnica per misurare la lunghezza degli archi di cerchio AP, un metodo matematico astratto, che non ricorra a uno strumento di misura "fisico", come un goniometro o una rotella misuratrice (vedi figura sotto a sinistra): ad es. (vedi figura sotto a destra) posso calcolare la lunghezza di poligonali che via via meglio approssimano il cerchio ricorrendo alle equazione del cerchio per determinarne i vertici. |
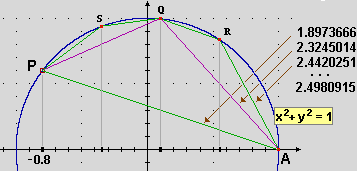
Nel caso del vettore (2,1) della
figura iniziale avrei ottenuto: 0.45950584, 0.46209331, 0.46307479, … 0.46364761,
0.46364761, …; 0.46364761 è l'arrotondamento a 8 cifre della direzione di (2,1), direzione che avevamo già rappresentato col versore (2/ 5,1/
5,1/ 5).
5).
La direzione dell'asse x è 0 (infatti il versore dell'asse x è OP con P = (1,0) = A); la direzione opposta, cioè la lunghezza 3.141592653589… del semicerchio che da A arriva a
|
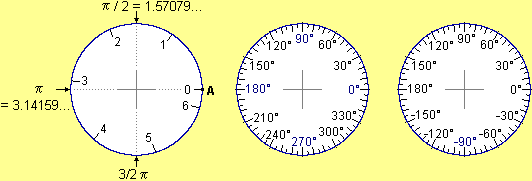
Questo (direzione del versore OP come lunghezza dell'arco AP) è il modo più usato in matematica e fisica per indicare le direzioni. Per passare ad esprimersi "come nel goniometro" (e nella bussola) si "definisce" grado la 180ª parte di π (traduzione dell'idea di suddividere il semicerchio con delle tacche in 180 divisioni): |
π
1° = ———
180 |
 figura soprastante)
invece delle direzioni π, π/2, 3/2π, … si parla anche
delle direzioni 180°, 90°, 270°, … .
figura soprastante)
invece delle direzioni π, π/2, 3/2π, … si parla anche
delle direzioni 180°, 90°, 270°, … .|
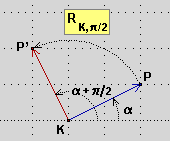
Dati un punto K e un numero φ
("fi"), la rotazione attorno a K di
ampiezza φ
(RK,φ)
è la funzione che a ogni punto P associa il punto P'
tale che il vettore KP' rispetto al vettore KP abbia lo stesso modulo e
direzione
variata di φ [vedi figura a destra, in cui φ è 90°].
Dati una semiretta a e un numero φ, con 0° ≤ φ ≤ 360°, l'unione delle semirette ottenute da a con rotazioni antiorarie attorno all'origine di a di ampiezza minore o uguale a φ viene chiamata angolo ab (e indicata  ab ab " si usa anche il simbolo "^"). L'origine di queste semirette viene chiamata vertice dell'angolo. Intuitivamente un angolo è una figura generata dalla rotazione di una semiretta attorno alla sua origine. " si usa anche il simbolo "^"). L'origine di queste semirette viene chiamata vertice dell'angolo. Intuitivamente un angolo è una figura generata dalla rotazione di una semiretta attorno alla sua origine.
|
 |