 è
opportuno cercare di capire, prima di mettersi a fare
manipolazioni, se è possibile risolvere l'equazione
direttamente, e, nel caso si debba procedere con manipolazioni,
scegliere le trasformazioni più convenienti (non esiste
un'unica ricetta per risolvere un'equazione!):
è
opportuno cercare di capire, prima di mettersi a fare
manipolazioni, se è possibile risolvere l'equazione
direttamente, e, nel caso si debba procedere con manipolazioni,
scegliere le trasformazioni più convenienti (non esiste
un'unica ricetta per risolvere un'equazione!):
2
t +1 = 0 | si
conclude subito che non ci sono soluzioni: qualunque sia t,
0≤t2 e, quindi, t2+1>0; |
a+1
——— = 1
a | si conclude subito che non ci
sono soluzioni: il rapporto tra numeri differenti non è
mai 1; |
x(x+1) = 0 | senza sviluppare x(x+1) in
x2+x si osserva: affinché il
prodotto tra x e x+1 sia 0 occorre (e basta) o che x sia 0 o che x+1 sia 0
(cioè x sia –1), per cui le soluzioni sono 0
e –1. |
 in
alcuni casi il problema che viene modellizzato mediante
l'equazione considerata impone delle restrizioni alla
variazione della incognita; occorre tenerne conto risolvendo
l'equazione:
in
alcuni casi il problema che viene modellizzato mediante
l'equazione considerata impone delle restrizioni alla
variazione della incognita; occorre tenerne conto risolvendo
l'equazione:
• ad esempio se in (20–2x)2x = 300
la variabile x rappresenta la lunghezza in cm di un oggetto lungo al
più 10 cm (come accadeva nel caso considerato  sopra), devo limitarmi a cercare le soluzioni in [0,10]; in altre parole il problema è modellizzato da: (20–2x)2x = 300 AND 0 ≤ x ≤ 10.
sopra), devo limitarmi a cercare le soluzioni in [0,10]; in altre parole il problema è modellizzato da: (20–2x)2x = 300 AND 0 ≤ x ≤ 10.
 l'esame
preventivo del dominio dell'equazione può far
risparmiare inutili manipolazioni;
l'esame
preventivo del dominio dell'equazione può far
risparmiare inutili manipolazioni;
•
ad esempio di fronte a  (–x) =
(–x) =  (x–1) posso osservare
che il primo membro è definito per x≤0, il secondo per
1≤x, e quindi, poiché l'equazione non è definita
per alcun x (x≤0 AND 1≤x è sempre falsa), non ha senso
cercare di risolverla.
(x–1) posso osservare
che il primo membro è definito per x≤0, il secondo per
1≤x, e quindi, poiché l'equazione non è definita
per alcun x (x≤0 AND 1≤x è sempre falsa), non ha senso
cercare di risolverla.
 una
equazione vera – cioè che, comunque si
sostituiscano numeri alle variabili (senza rendere indefiniti i
termini che compaiono in essa), risulta vera – viene detta anche
identità; una equazione falsa –
cioè che, comunque si sostituiscano numeri …, risulta
falsa – in qualche libro è chiamata equazione impossibile
(nel senso che è impossibile trovare soluzioni perché
non ne esistono, non perché non si è capaci di
trovarle);
una
equazione vera – cioè che, comunque si
sostituiscano numeri alle variabili (senza rendere indefiniti i
termini che compaiono in essa), risulta vera – viene detta anche
identità; una equazione falsa –
cioè che, comunque si sostituiscano numeri …, risulta
falsa – in qualche libro è chiamata equazione impossibile
(nel senso che è impossibile trovare soluzioni perché
non ne esistono, non perché non si è capaci di
trovarle);
2
2x
———— = 2x
x | è un'identità poiché è vera per tutti gli
x per cui è definita (cioè per ogni x diverso da 0); tuttavia
i due membri dell'equazione non sono  algebricamente equivalenti
in quanto hanno domini diversi; algebricamente equivalenti
in quanto hanno domini diversi; |
 (–x) = (–x) =  x x | è un'identità poiché è vera per tutti gli
x per cui è definita (cioè per x=0); |
2
t +1 = 0 | è falsa poiché t2+1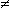 0
per ogni t; 0
per ogni t; |
 la
quantità delle soluzioni di un'equazione può
variare da caso a caso:
la
quantità delle soluzioni di un'equazione può
variare da caso a caso:
• le equazioni false hanno 0
soluzioni;
• le equazioni vere possono avere un
numero di soluzioni infinito (come nel primo esempio del punto
precedente) o finito (come nel secondo esempio);
• l'equazione |2x+1|–|x–1|–x = k, risolta rispetto a x, può avere 0, 1, 2 o infinite
soluzioni a seconda del valore di k:
 dopo
la risoluzione di un'equazione attraverso manipolazioni, è
utile verificare se le soluzioni trovate sono
effettivamente soluzioni, cioè se, sostituite alla variabile
assunta come incognita, rendono vera l'equazione: nel corso delle
manipolazioni potrebbero essersi verificati degli errori; ad es. se dopo la seguente risoluzione di equazione:
dopo
la risoluzione di un'equazione attraverso manipolazioni, è
utile verificare se le soluzioni trovate sono
effettivamente soluzioni, cioè se, sostituite alla variabile
assunta come incognita, rendono vera l'equazione: nel corso delle
manipolazioni potrebbero essersi verificati degli errori; ad es. se dopo la seguente risoluzione di equazione:
2 2 2 2 2 2
12 + ——— = 3x + ——— —> 12 + ——— — ——— = 3x + ——— — ——— —> 12=3x —> x=4
x-4 x-4 | x-4 x-4 x-4 x-4 | |
| |
2 | applico /3 e
applico - ——— semplifico ——
x-4 inverto l'eq.
verifico quanto ottenuto sostituendo 4 a x nell'equazione
originale, ottengo:
2 2 2 2
12 + ——— = 3·4 + ——— —> 12 + — = 12 + —
4-4 4-4 0 0che non è definita.
 è
opportuno cercare di capire, prima di mettersi a fare
manipolazioni, se è possibile risolvere l'equazione
direttamente, e, nel caso si debba procedere con manipolazioni,
scegliere le trasformazioni più convenienti (non esiste
un'unica ricetta per risolvere un'equazione!):
è
opportuno cercare di capire, prima di mettersi a fare
manipolazioni, se è possibile risolvere l'equazione
direttamente, e, nel caso si debba procedere con manipolazioni,
scegliere le trasformazioni più convenienti (non esiste
un'unica ricetta per risolvere un'equazione!):
 (–x) =
(–x) = 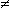 0
per ogni t;
0
per ogni t; |2x+1|–|x–1|–x, riprodotto a lato, interseca la
retta orizzontale y=k:
|2x+1|–|x–1|–x, riprodotto a lato, interseca la
retta orizzontale y=k:
 )
) {–2}
{–2}