|
Elementary Vector Analysis
In order to measure many physical quantities, such as force or
velocity, we need to determine both a magnitude and a direction. Such
quantities are conveniently represented as vectors.
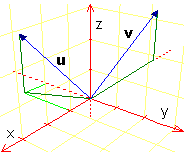
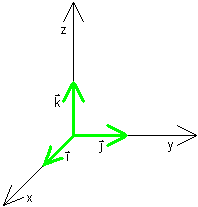 The direction of a vector v in 3-space is specified by its
components in the x, y, and z directions, respectively:
The direction of a vector v in 3-space is specified by its
components in the x, y, and z directions, respectively:
(x,y,z) or xi + yj + zk,
i = (1,0,0)
j = (0,1,0)
k = (0,0,1)
|
where i, j, and k are the coordinate vectors
along the x-, y-, and z-axes.
The magnitude of a vector v = (x,y,z), also called its
length or norm, is given by
Notes
- Vectors can be defined in any number of dimensions, though we
focus here only on 3-space.
- When drawing a vector in 3-space, where you position the vector
is unimportant; the vector's essential properties are just its
magnitude and its direction. Two vectors are equal if and only
if corresponding components are equal.
- A vector of norm 1 is called a unit vector. The
coordinate vectors are examples of unit vectors.
- The zero vector, 0 = (0,0,0), is the only vector with
magnitude 0.
Basic Operations on Vectors
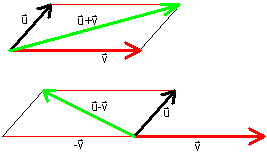 To add or subtract vectors
u = (u1,u2,u3) and
v = (v1,v2,v3),
To add or subtract vectors
u = (u1,u2,u3) and
v = (v1,v2,v3),
add or subtract the corresponding coordinates:
u + v = (u1+v1,u2+v2,u3+v3)
u - v = (u1-v1,u2-v2,u3-v3)
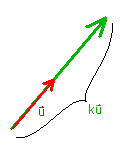 To mulitply vector u by a scalar k, multiply each coordinate
of u by k:
To mulitply vector u by a scalar k, multiply each coordinate
of u by k:
k u = (ku1,ku2,ku3)
Example
The vector v = (2,1,-2) = 2i + j - 2k
has magnitude
|
|| |
v |
|| = |
| ___________
√22 +12 -(-2)2
|
= 3. |
|
Thus, the vector 1/3v =
(2/3,1/3,-2/3) is a unit vector in the same direction as v.
In general, for v ≠
0, we can scale (or normalize)
v to the unit vector v/ ||v||
pointing in the same direction as v.
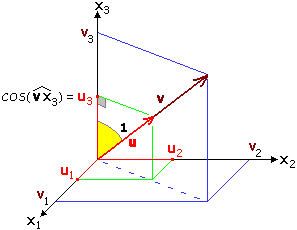
Le componenti del versore (vettore unitario) u ottenuto normalizzando v = (v1,v2,v3) vengono dette anche coseni direttori
(direction cosines) di v in quanto sono dati dal coseno degli angoli che v forma con i tre assi coordinati:
ui = cos(∠ v xi) (avendo indicato gli assi x, y e z con x1,
x2 e x3).
La figura a lato illustra il caso di u3. Con un'analoga costruzione si possono illustrare gli altri due casi.
Si noti che posso scrivere sia cos(∠ v xi) che cos(∠ xi v) in quanto cos(α) = cos(–α).
|  |
|
Una somma del tipo
a1v1+a2v2+…+anvn
(con ai numeri reali e vi vettori) viene detta combinazione lineare
dei vettori v1, v2, …, vn.
Ogni vettore può essere espresso (in modo unico) come combinazione lineare di i, j e k.
|
Dot Product (prodotto scalare)
Let u = (u1,u2,u3)
and v = (v1,v2,v3).
The dot product u · v
(also called the scalar procuct or Euclidean inner
product) of u and v is defined in two distinct
(though equivalent) ways:
|
| |
|
|
|
|
|
|
|
|
|
| where 0 ≤ θ ≤ π is the angle between |
u |
and |
v |
|
|
| |
| 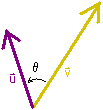 |
Why are the two definitions equivalent?
Properties of the Dot Product
- u · v = v · u
- u · (v + w) = (u · v) + (u · w)
- u · u = || u ||2
See if you can verify each of these!
Example
 If u = (1,-2,2) and v = (-4,0,2), then
If u = (1,-2,2) and v = (-4,0,2), then
Using the second definition of the dot product with || u || = 3 and || v || = 2√5,
so cosθ = 0, yielding θ = π/2.
Though we might not have guessed it, u and v are
perpendicular to each other!
In general,
Two non-zero vectors u and v are
perpendicular (or orthogonal) if and only if
u ·v = 0.
Proof
Projection of a Vector
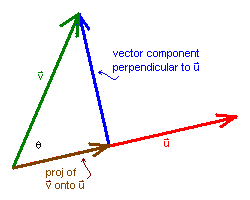 It is often useful to resolve a vector v into the sum of
vector components parallel and perpendicular to a vector u.
It is often useful to resolve a vector v into the sum of
vector components parallel and perpendicular to a vector u.
Consider first the parallel component, which is called the
projection of v onto u. This projection should be in
the direction of u and should have magnitude ||v||cosθ, where 0 ≤ θ ≤ π is the angle between
u and v. Let's normalize u to
u/|| u || and then scale this by
the magnitude || v ||cosθ:
|
Projection of v onto u
|
|
| |
| = |
||v||
||u||
cosθ
||u||2
|
u |
|
|
|
The perpendicular vector component of v is then just the
difference between v and the projection of v onto
u.
In summary,
| projection of v onto u: |
|
vector component of v
perpendicular to u:
|
|
|
Cross Product (prodotto vettoriale)
Let u = (u1,u2,u3) and v = (v1,v2,v3).
The cross product (also called the vector product) u × v yields a vector perpendicular to both u and v
with direction determined by the right-hand rule. Specifically,
u × v =
(u2v3-u3v2)i -
(u1v3-u3v1)j +
(u1v2-u2v1)k
| or: u × v = |
|
|
|
|
| |
|
i | | j | | k |
| |
|
|
|
| |
| ux | uy | uz |
| vx | vy | vz |
It can also be shown that
|| u × v
|| =
|| u
|| ||
v
|| sinθ
for u ≠ 0,
for v ≠ 0
where 0 ≤
θ
≤
π
is the angle between
u and v.
Proof
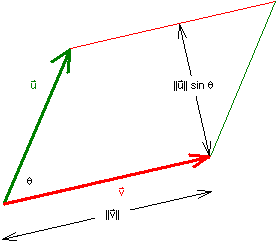 Thus, the magnitude || u ×v || gives
the area of the parallelogram formed by u and v.
Thus, the magnitude || u ×v || gives
the area of the parallelogram formed by u and v.
As implied by the geometric interpretation,
Non zero vectors u and v are
parallel if and only if u × v = 0.
Proof
Properties of the Cross Product
- u × v = - ( v × u)
- u × ( v + w ) = (u × v ) + ( u × w )
- u × u = 0
Again, see if you can verify each of these.
Connections between the dot product and cross product (Lagrange's Identity)
Key Concepts [index]
Let u = (u1,u2,u3) and v = (v1,v2,v3).
- Basic Operations, Norm of a vector
- Dot Product
|
| |
|
|
|
|
|
|
|
|
| where 0 ≤ θ
≤
π
is the angle between u and v |
|
| |
|
For u ≠
0, v ≠
0, u · v = 0 if and only if u is
orthogonal to v.
- Projection of a Vector
| projection of v onto u: |
|
vector component of v
perpendicular to u:
|
|
- Cross Product
u × v =
(u2v3-u3v2)i -
(u1v3-u3v1)j +
(u1v2-u2v1)k
|| u × v
|| =
|| u
|| || v
|| sinθ
for u ≠ 0,
for v ≠ 0
where 0 ≤
θ
≤
π is the angle between
u and v.
For u ≠
0, v ≠
0, u × v = 0 if and only if u is
parallel to v.
|
 The direction of a vector v in 3-space is specified by its
components in the x, y, and z directions, respectively:
The direction of a vector v in 3-space is specified by its
components in the x, y, and z directions, respectively:
 To add or subtract vectors
u = (u1,u2,u3) and
v = (v1,v2,v3),
To add or subtract vectors
u = (u1,u2,u3) and
v = (v1,v2,v3),
 To mulitply vector u by a scalar k, multiply each coordinate
of u by k:
To mulitply vector u by a scalar k, multiply each coordinate
of u by k:






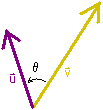
 If u = (1,-2,2) and v = (-4,0,2), then
If u = (1,-2,2) and v = (-4,0,2), then
 It is often useful to resolve a vector v into the sum of
vector components parallel and perpendicular to a vector u.
It is often useful to resolve a vector v into the sum of
vector components parallel and perpendicular to a vector u.
 Thus, the magnitude || u ×v || gives
the area of the parallelogram formed by u and v.
Thus, the magnitude || u ×v || gives
the area of the parallelogram formed by u and v.