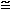 "
"Il termine "uguale" e il simbolo "=" sono usati in molti modi in matematica, spesso diversi da quelli impiegati nel linguaggio comune.
Prova a fare una rassegna di questi usi e a discutere i problemi didattici connessi, a partire dalla scuola di base.
Nel linguaggio comune uguale ha diversi signficati: • sono uguali come gocce d'acqua (non differiscono fisicamente in nulla); • è sempre uguale (non muta al variare delle condizioni e delle situazioni); • la scuola deve offrire uguali opportunità a tutti i bambini (non devono differire qualunque sia la razza, la religione, il sesso, la condizione economica); • ha uno stile uguale (equilibrato, coerente); • ha una voce sempre uguale (senza cambiamenti nel tono e nel volume); ...
In matematica indica una relazione tra enti che, in un certo contesto, godono delle stesse proprietà; non significa, né nella lingua comune né in matematica, che sono la stessa cosa. In diversi libri di testo italiani della scuola di base, invece, si trovano frasi del tipo "in matematica si dice che due oggetti sono uguali se sono la stessa cosa; due gemelli un matematico non direbbe mai che sono uguali: non si tratta della stessa persona", dimostrando l'ignoranza dei loro autori (e dell'ignoranza o della colpevole superficialità degli insegnanti che li adottano).
Precisando, in matematica l'eguaglianza è sostanzialmente una relazione di equivalenza, la cui verità o falsità dipende dal contesto in cui ci si pone: • 3 e 6/2 sono termini diversi, ma sono eguali come valori numerici, • due quadrati sovrapponibili ma non sovrapposti sono figure distinte ma sono eguali rispetto ai movimenti, due triangoli uno rettangolo e l'altro equilatero sono diversi rispetto ai movimenti ma sono eguali dal punto di vista proiettivo (alla vista, posizionandomi in posizioni opportune, ogni triangolo assume lo stesso aspetto); • anche x+5−x e 5 sono espressioni diverse ma sono algebricamente equivalenti (o eguali …).
Altri esempi: • le espressioni 007 e 7 sono due diverse "stringhe" (ossia due diverse sequenze di simboli) ma sono da intendersi uguali come numeri; • anche 0 e
Vi sono poi due diversi usi del simbolo "=" (che come vedremo hanno anche dei collegamenti con l'insegnamento nella scuola di base), nelle assegnazioni e nelle approssimazioni.
Le assegnazioni sono modi per indicare il valore da attribuire ad una variabile; ad esempio per indicare che alla variabile x diamo il valore 5 possiamo usare, a seconda delle convenzioni usate, una delle seguenti scritture: x = 5, x := 5, x ← 5 (ed anche 5 → x). Le assegnazioni non sono simmetriche come le equazioni (5 = x o 5 → x non rappresentano delle assegnazioni) e ad una variabile può essere assegnato un termine contenente la stessa variabile: ad esempio le assegnazioni x = x+1 e A = 5/A indicano il nuovo valore da attribuire alle variabili a partire da quello che avevano finora.
Nel calcolo numerico scriviamo ad esempio 20/3 = 6.6666667. Scritture analoghe sono usate dai mezzi di calcolo. Con ciò intendiamo dire che 20/3 ha come valore arrotondato 6.6666667, non che vale esattamente 6.6666667, cioà che 20/3 = 6.6666667000…
In questi casi al posto di "=" si può usare "≈" o  "
"
Si usano anche notazioni come: x = 3.2 ± 0.1. Ciò non significa "x = 3.2+0.1 o x = 3.2–0.1": si tratta di un'abbreviazione per: 3.2–0.1 ≤ x ≤ 3.2+0.1.
Le considerazioni fatte finora non erano rivolte direttamente all'insegnamento, ma hanno messo a fuoco la polisemia della parola "uguale" e del simbolo "=". Di essa dobbiamo invetitabilmente tener conto anche a livello didattico.
Partiamo da un esempio. In genere gli alunni hanno maggiori difficoltà di fronte a problemi del tipo 9 = 3+? rispetto a problemi equivalenti del tipo 3+? = 9. Perché? Il contesto delle attività aritmetiche proposte a scuola spesso induce negli alunni l'interpretazione di "=" invece che come simbolo di "identità" come simbolo per indicare il risultato. Ciò è messo in luce anche da errori del tipo 30+50 = 80·2 = 160 … che, invece, andrebbe scritto:
Che fare? Bisogna educare gli alunni ai diversi usi, nei vari contesti, del simbolo "=" (come accade e accadrà in classi successive anche per altri simboli matematici), occorre usare anche grafi (come nell'esempio precedente), diagrammi di flusso e script (vedi i molti esempi presenti qui), …
Nell'uso dei grafi per rappresentare le addizioni occorre distinguere il caso in cui l'operazione viene percepita come unaria, cioè a un solo argomento ("oggi è il 15; che data avremo fra 3 giorni?"; si veda la seguente illustrazione a sinistra, in cui 15 e 3 non possono essere percepiti in modo simmetrico: il primo funziona come dato di partenza, sul quale il secondo opera una trasformazione) da quello in cui è intesa come un'operazione binaria che opera simultaneamente su due argomenti ("metto insieme 15 e 3 euro; quanto ho in tutto?"; si veda l'illustrazione a destra).
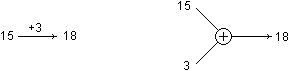
Per inciso, osserviamo che anche nell'educazione alla scrittura sorgono problemi legati all'uso di simboli uguali o no a seconda del contesto interpretativo.
Innanzitutto osserviamo che le lettere sono figure che vengono sempre considerate in relazione ad un sistema di riferimento fissato:
questo è determinato da linee o quadretti già tracciati sul foglio o da parole già scritte o …
Ad esempio la lettera C, anche se può avere stessa forma
della U, tanto da essere ad essa sovrapponibile con un movimento piano, non è (come lettera) ad essa uguale in quanto
è diversamente inclinata rispetto alla linea di scrittura; lo stesso vale per b e q, per d e p, per n
e u, per N e Z, e anche per le cifre 6 e 9. Il concetto di eguaglianza che si viene così a formare
probabilmente è in parte all'origine delle difficoltà che in anni successivi gli alunni incontrano nel riconoscere come
eguali figure geometriche sovrapponibili ma diversamente orientate.
Il bambino distingue facilmente le lettere sopra considerate. Ha maggiori difficoltà nel distinguere lettere simmetriche (rispetto a un
asse perpendicolare alla linea di scrittura) come d e b, q e p, e le "quasi" simmetriche S e Z;
ciò è evidentemente connesso anche a problemi
psicomotori, che si manifestano anche in forme di inversione nella scrittura di alcune lettere e cifre.
Nel correggere gli errori di scrittura/lettura è bene che
l'insegnante tenga conto della relatività del concetto di
eguaglianza e dei conflitti interpretativi a cui le sue osservazioni
possono dare luogo; in questo senso può invece essere utile
che egli mostri come da una lettera si può passare ad un'altra
con una rotazione piana o con un ribaltamento. La focalizzazione contestuale di queste
proprietà geometriche può favorire la formazione nell'alunno di schemi mentali che lo aiutino ad acquisire una
maggiore padronanza della lettura e della scrittura.
Ovviamente, occorre educare gli alunni alla scrittura sia in stampatello che in corsivo ...