Con la seguente riga di istruzioni in R o simili con altri linguaggi:
if(runif(1)< 1/4) runif(1)*10 else runif(1)*20
simulo una particolare variabile casuale U
che può essere pensata come modello della distribuzione della caratteristica U di una popolazione
costituita dall'unione di due sottopopolazioni (una il triplo dell'altra) nelle quali U è distribuita
uniformemente, in un caso in [0,20), nell'altro in [0,10).
Qual è il grafico della funzione di densità di U? Quali ne sono media e mediana?
Quale può essere una formulazione della funzione di densità?
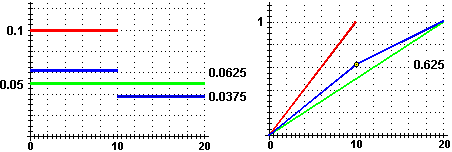
Sotto sono raffigurati i grafici delle funzioni di densità F (F(x) = 1/10)
e G (G(x) = 1/20) delle distribuzioni uniformi in [0,10] e in [0,20] e il grafico della funzione
densità H di U (H(x) = F(x)/4+3/4·G(x),
avendo prolungato F con valore 0 al di fuori del suo dominio), che è a scalini:
H(x) = 1/16 per x tra 0 e 10 (escluso), H(x) = 3/80 per x tra 10 e 20
(l'area sottesa è effettivamente 1: 10/16+30/80 = 50/80+30/80 = 80/80 = 1). La mediana è il valore M tale che
1/16*M = 1/2, ossia 8.
 | [a destra sono rappresentate anche le funzioni di ripartizione] |
Per trovare la media possiamo ragionare "fisicamente":
il baricentro del primo rettangolo in cui è spezzabile l'area sottesa ad H ha ascissa 5, quello del secondo ha ascissa 15; quindi il baricentro complessivo ha ascissa
5·50/80+15·30/80 = (25+45)/8 = 70/8 = 8.75.
Ovvero potevo calcolare l'integrale tra 0 e 20 della funzione che a x associa x·H(x).
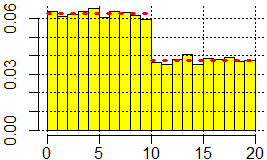
Sotto lo studio sperimentale con R:
U <- NULL for(i in 1:2e4) U[i] <- if(runif(1)< 1/4) runif(1)*10 else runif(1)*20 hist(U,probability=TRUE,col="yellow") abline(h=axTicks(2),v=axTicks(1),lty=3) lines(c(0,10),c(1/16,1/16),col="red",lty=3,lwd=3) lines(c(10,20),c(3/80,3/80),col="red",lty=3,lwd=3) mean(U) # 8.747563 |
 |
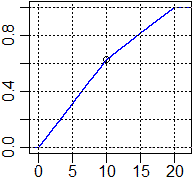
# Ecco anche il grafico della funzione di ripartizione (ecdf # sta per "empirical cumulative distribution function") plot(ecdf(U), do.points=FALSE, col="blue") abline(h=axTicks(2),v=axTicks(1),lty=3) points(10, 0.625) |
 |
[per un esercizio con analogie vedi il 3.7]
Se clicchi qui
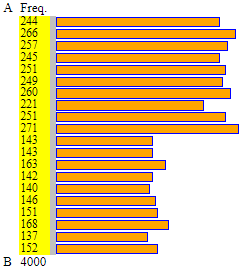
puoi accedere alla generazione in JavaScript di una simulazione del fenomeno, con 4000 valori.
Sotto lo studio, realizzato con
questo script, di un possibile esito (studio che conferma che la mediana è 8, e il primo quartile 4).