Calcolo approssimato
 Spesso
di un numero reale X non conosciamo tutte le cifre, ma solo
un'approssimazione per difetto e un'approssimazione per eccesso. Ciò
può accedere, ad esempio, se X è la
Spesso
di un numero reale X non conosciamo tutte le cifre, ma solo
un'approssimazione per difetto e un'approssimazione per eccesso. Ciò
può accedere, ad esempio, se X è la  misura di
una grandezza fisica ottenuta attraverso la lettura di uno strumento
di misurazione
o se X è stato precedentemente sottoposto a un
misura di
una grandezza fisica ottenuta attraverso la lettura di uno strumento
di misurazione
o se X è stato precedentemente sottoposto a un  arrotondamento
e noi non conosciamo il valore originale.
arrotondamento
e noi non conosciamo il valore originale.
L'intervallo che ha per estremi
l'approssimazione per difetto e l'approssimazione per eccesso viene
detto intervallo di indeterminazione di X e l'ampiezza
di questo intervallo viene chiamata indeterminazione
(o incertezza) di X: quanto più piccola è
l'indeterminazione tanto meno indeterminata (cioè tanto più
precisa) è la nostra conoscenza di X.
|
 Consideriamo,
per esempio, una bilancia con il quadrante ripartito in 65
divisioni uguali; ogni divisione rappresenti la variazione di un
chilogrammo, in modo che con la bilancia si possano misurare pesi
di al più 65 kg. Consideriamo,
per esempio, una bilancia con il quadrante ripartito in 65
divisioni uguali; ogni divisione rappresenti la variazione di un
chilogrammo, in modo che con la bilancia si possano misurare pesi
di al più 65 kg.
Supponiamo che la bilancia abbia la
precisione di 1 kg, cioè che la misura vera possa scostarsi al più
di 1 kg dalla misura letta sul quadrante [negli esempi alla voce modello si è già considerata la  precisione di un termometro]. precisione di un termometro].
Se, pesando un oggetto, la tacca 44 è
quella più vicina alla posizione finale dell'ago, possiamo
concludere che il peso P dell'oggetto (in kg) è compreso
tra 44–1=43 e 44+1=45:
43 ≤ P ≤ 45,
cioè: P ∈
[43, 45].
|
 |
| |
Nota:
il simbolo "∈"
viene usato come abbreviazione di "appartiene a"
o "sta in" o "è un elemento di"
o …; è una deformazione della lettera "E"
(iniziale di "elemento").
[43,45] è l'intervallo di
indeterminazione di P. L'indeterminazione è 45–43=2. Non
conosciamo esattamente il numero P, ma conosciamo un'intervallo ampio
2 che lo contiene.
Gli strumenti graduati sono in genere costruiti in modo che l'ampiezza di una divisione corrisponda alla sensibilità dello strumento, ossia alla minima variazione della grandezza misurata che fa variare il valore indicato dallo strumento; in questi casi precisione e sensibilità possono essere considerati come sinonimi. Ma non è sempre così: in alcuni casi al più piccolo stimolo che lo strumento percepisce il valore indicato si modifica di più di una divisione; un fenomeno analogo si verifica spesso con gli strumenti in cui le misure sono espresse digitalmente: per misure di un certo ordine di grandezza alla più piccola variazione le ultime cifre variano di molte unità (in questi casi la precisione dello strumento può essere molto maggiore, ossia molto peggiore, rispetto al valore che corrisponde alle variazioni della cifra più a destra), mentre per misure di altri ordini di grandezza lo stesso strumento si può comportare in maniera opposta (l'ultima cifra scatta più lentamente rispetto alle variazioni che lo strumento in realtà percepisce). In alcuni libri di testo viene usato il termine "sensibilità" al posto di quello di "precisione" anche nelle situazioni in cui non è ad esso equivalente. |
|
In fisica spesso si fa una distinzione tra misura
precisa e misura accurata: una misura x
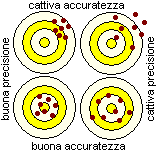
con ideterminazione Δx di una grandezza x è tanto più accurata quanto più x è vicino al valore esatto di x, è tanto più precisa quanto più Δx è piccolo. Questa distinzione rende conto del fatto che, in una attività di misurazione, possono essere presenti degli errori sistematici, dovuti ad un difetto di impostazione [ad esempio l'uso di una bilancia ad ago in cui l'ago a riposo non è posizionato su 0 o di una riga graduata in cui le divisioni sono più ampie del dovuto], che fanno sì che le misure ottenute, per quanto "precise", siano comunque affette da uno scarto dal valore esatto. In questa voce, quando facciamo degli esempi riferiti alla fisica, supponiamo sempre che si tratti di misure accurate, ossia che le approssimazioni siano effettive approssimazioni del valore esatto. La figura a lato illustra metaforicamente il comportamento di apparati misuratori molto sensibili con diversi gradi di precisione e accuratezza (i valori esatti sono il "centro" dei bersagli).
|  |
|
 Di
fronte alla percentuale 43.7%, sapendo che si tratta di un valore
che è stato arrotondato, possiamo
dire che il valore originale cade tra 43.65 e 43.75. Di
fronte alla percentuale 43.7%, sapendo che si tratta di un valore
che è stato arrotondato, possiamo
dire che il valore originale cade tra 43.65 e 43.75.
La precisione è 0.05 (il
valore originale può al massimo variare di 0.05, in più
o in meno, da 43.7).
L'indeterminazione
è 0.1: è questa l'ampiezza dell'intervallo in cui
può cadere il valore originale.
|
 |
|
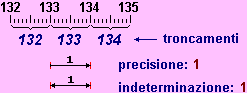
 Di
fronte al tempo 133 sec, sapendo che è una misura troncata
ai secondi, possiamo dire che la misura esatta, in secondi, cade
tra 133 e 134. Di
fronte al tempo 133 sec, sapendo che è una misura troncata
ai secondi, possiamo dire che la misura esatta, in secondi, cade
tra 133 e 134.
La precisione è 1 (il
valore esatto può al massimo variare di 1, in più,
da 133).
L'indeterminazione
è 1: è questa l'ampiezza dell'intervallo in cui può
cadere il valore esatto.
|
 |
 Nel
caso di valori esatti, ad esempio se so che x=3.2
esattamente (cioè che x=3.2000…), posso dire che
l'indeterminazione è 0. Infatti l'intervallo che
contiene solo 3.2 è l'intervallo [3.2, 3.2], che ha ampiezza 0.
Nel
caso di valori esatti, ad esempio se so che x=3.2
esattamente (cioè che x=3.2000…), posso dire che
l'indeterminazione è 0. Infatti l'intervallo che
contiene solo 3.2 è l'intervallo [3.2, 3.2], che ha ampiezza 0.
|
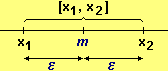
 Invece di x ∈ [x1, x2]
si scrive anche x = m ± ε,
dove m è il valore a metà dell'intervallo
[x1,x2]
e ε
(epsilon) è la sua semiampiezza, cioè: m–ε = x1,
m+ε = x2. Invece di x ∈ [x1, x2]
si scrive anche x = m ± ε,
dove m è il valore a metà dell'intervallo
[x1,x2]
e ε
(epsilon) è la sua semiampiezza, cioè: m–ε = x1,
m+ε = x2.
Con
questa notazione nel caso dei quattro esempi precedenti posso
scrivere: P = 44±1, percentuale = 43.7±0.05,
tempo = 133.5±0.5, x = 3.2±0.
|
 |
| |
Nota. A volte viene usato il termine errore al posto di quello di precisione.
Ad esempio, nel caso che in una misurazione si ottenga 37±2 cm, invece di dire che la misura 37 cm ha una precisione di 2 cm, si può sentir dire che "ha un errore di 2 cm".
Questo, dal punto di vista matematico, è scorretto in quanto l'errore è la differenza ValoreApprossimato – ValoreEsatto.
Supponiamo per es. che LunghezzaEsatta = 36.24000… cm
(anche se sappiamo  che a rigore non ha senso parlare di lughezza esatta di un oggetto).
In questo caso 37 cm è una approssimazione per eccesso, ossia con un errore positivo: Errore = (37–36.24000…) cm = 0.76000… cm. che a rigore non ha senso parlare di lughezza esatta di un oggetto).
In questo caso 37 cm è una approssimazione per eccesso, ossia con un errore positivo: Errore = (37–36.24000…) cm = 0.76000… cm.
Se invece LunghezzaEsatta = 37.48000… cm, 37 cm sarebbe una approssimazione per difetto, ossia con un errore negativo: Errore = (37–37.48000…) cm = –0.52000… cm.
Di fronte a 37±2 cm potremmo invece dire che l'errore è al più di 2 cm (in valore assoluto). In altre parole la precisone è una
valutazione del valore assoluto massimo dell'errore.
Si tenga comunque presente che molti fisici usano il termine "errore" al posto di quello di "precisione", e usano questo secondo termine per indicare quella che i matematici chiamano "precisione relativa", ossia il rapporto tra precisione e valore approssimato del numero (vedi le considerazioni sulla "indeterminazione relativa" svolte poco sotto).
In questo, come in molti altri casi, è dal contesto che dobbiamo capire come i termini "errore" e "precisione" sono usati.
|
 Come faccio a eseguire operazioni tra
numeri che conosco solo in modo approssimato?
Come faccio a eseguire operazioni tra
numeri che conosco solo in modo approssimato?
I procedimenti che si impiegano per
affrontare queste situazioni vengono chiamati "metodi di calcolo
approssimato" (a volte, nelle scienze sperimentali, si parla invece di "studio della
propagazione degli errori"). Abbiamo già visto qualche esempio di
calcolo approssimato nel caso particolare dei  calcoli mentali:
arrotondati a 1 o 2 cifre i dati iniziali, si eseguono i calcoli su
queste approssimazioni e si prende il risultato arrotondato a 1
cifra: 768·426 ≈ 800·400 = 320000 ≈ 300 000.
calcoli mentali:
arrotondati a 1 o 2 cifre i dati iniziali, si eseguono i calcoli su
queste approssimazioni e si prende il risultato arrotondato a 1
cifra: 768·426 ≈ 800·400 = 320000 ≈ 300 000.
Abbiamo introdotto qualche considerazione più generale discutendo come  definire le operazioni tra numeri reali.
definire le operazioni tra numeri reali.
Affrontiamo la questione in modo più
sistematico.
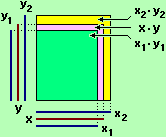
 x1 ≤ x ≤ x2
e => x1+y1 ≤ x+y ≤ x2+y2
y1 ≤ y ≤ y2
x1 ≤ x ≤ x2
e => x1+y1 ≤ x+y ≤ x2+y2
y1 ≤ y ≤ y2
|
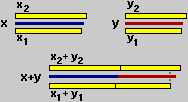 |
Es.: Un
campo di forma triangolare ha lati le cui misure in metri sono a=46,
b=38, c=51. Sappiamo che si tratta approssimazioni con
la precisione di 1 (metro), cioè che, ad essere più
rigorosi: a∈[45,47],
b∈[37,39],
c∈[50,52].
Che cosa possiamo concludere sul perimetro del campo?
a+b+c∈[45+37+50,47+39+52]
= [132,138], cioè: 132 m ≤ perimetro ≤
138 m |
| Possiamo
anche scrivere: perimetro = 135 ± 3 m |
132 135 138
—+—+—+—+—+—+—+—
|—————|—————|
3 3 |
 0 ≤ x1 ≤ x ≤ x2
e => x1·y1 ≤ x·y ≤ x2·y2
0 ≤ y1 ≤ y ≤ y2
0 ≤ x1 ≤ x ≤ x2
e => x1·y1 ≤ x·y ≤ x2·y2
0 ≤ y1 ≤ y ≤ y2
Es.: Ho
a disposizione i seguenti dati: la popolazione P della
città X è di 89 mila abitanti e il 37.2% di essa ha
più di 50 anni. Qual è il numero A degli
abitanti con più di 50 anni? |
 |
Si
tratta di dati arrotondati, cioè:
P ∈ [88.5 mila, 89.5 mila], percentuale ∈ [37.15, 37.25].
Quindi:
A = P·percentuale ∈ [88.5 mila · 37.15%, 89.5 mila · 37.25%] =
= [32.87775 mila, 33.33875 mila]
|
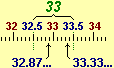
| Posso
dire che A è tra 32 mila 800 e 33 mila 400. Poiché
si tratta di un intervallo contenuto nell'intervallo che
corrisponde all'arrotondamento a 33 mila (vedi figura a lato), per
essere più sintetici, pur perdendo qualche informazione,
posso arrotondare A con 33 mila. |
 |
Mentre nel caso delle addizioni
e in quello delle moltiplicazioni (tra numeri positivi)
l'approssimazione per difetto [per eccesso] del risultato è la
somma o il prodotto delle approssimazioni per difetto [per eccesso]
dei dati di partenza, nel caso delle sottrazioni e
delle divisioni occorre operare "incrociando"
approssimazioni per difetto e per eccesso dei due dati di partenza.
Ciò accade perché sottrarre
equivale ad addizionare l'opposto [ trasformare differenza
trasformare differenza  somma] e dividere equivale a
moltiplicare per il reciproco [
somma] e dividere equivale a
moltiplicare per il reciproco [ trasformare rapporto
trasformare rapporto  prodotto],
e il passaggio all'opposto e al reciproco invertono la relazione
d'ordine tra i numeri:
prodotto],
e il passaggio all'opposto e al reciproco invertono la relazione
d'ordine tra i numeri:
 x1 ≤ x ≤ x2 => - x2 ≤ -x ≤ -x1
x1 ≤ x ≤ x2 => - x2 ≤ -x ≤ -x1
Es.: Se
A = 1.5±2, cioè A ∈ [1.3, 1.7],
posso concludere che –A = –1.5±2, cioè
–A ∈ [–1.7, –1.3]. |
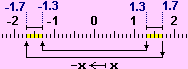 |
 Es.: La
temperatura in °C nella località W in un certo giorno
ha avuto come valore minimo m=12 e come valore massimo
M=24. Sapendo
che queste misure hanno la precisione di 1°, come possiamo
approssimare l'escursione termica, cioè M–m?
Dobbiamo calcolare M–m, cioè M+(–m).
Es.: La
temperatura in °C nella località W in un certo giorno
ha avuto come valore minimo m=12 e come valore massimo
M=24. Sapendo
che queste misure hanno la precisione di 1°, come possiamo
approssimare l'escursione termica, cioè M–m?
Dobbiamo calcolare M–m, cioè M+(–m).
23≤M≤25 23≤M≤25
e => e => 10 = 23 + -13 ≤ M + -m ≤ 25 + -11 = 14
11≤m≤13 -13≤-m≤-11
Concludendo:
10° ≤ escursione ≤ 14°, ovvero:
escursione = 12°±2°.
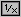 1 1 1
0 < x ≤ x ≤ x => —— ≤ — ≤ ——
1 2 x x x
2 1
1 1 1
0 < x ≤ x ≤ x => —— ≤ — ≤ ——
1 2 x x x
2 1
In altre parole, dividere per un numero più grosso dà luogo a un risultato più piccolo.
Quindi (vedi fig. a lato) se x ∈ [0.5, 3] il suo reciproco 1/x sta in [1/3, 2]. |
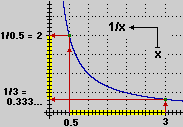
al crescere di x il valore
di 1/x diminuisce |
Es.: So
che vale la relazione B=kA, dove k=1.9 (valore
arrotondato). Voglio trasformare la relazione nella forma A=hB.
Come posso approssimare h?
1 1 1 1
B=kA <=> A=—B 1.85≤k≤1.95 => 0.512…= ———— ≤ h=— ≤ ———— = 0.540…
k 1.95 k 1.85
 Es.: In una
pubblicazione dell'ISTAT si trova che il Lussemburgo, nel 1990, aveva
popolazione P di 381 mila abitanti, densità D di 147 ab./km2
e superficie S di 3 mila km2.
Per trovare con più precisione la superficie possiamo usare gli altri due dati,
e ricorrere alle strategie messe a punto per
× e
1/x:
Es.: In una
pubblicazione dell'ISTAT si trova che il Lussemburgo, nel 1990, aveva
popolazione P di 381 mila abitanti, densità D di 147 ab./km2
e superficie S di 3 mila km2.
Per trovare con più precisione la superficie possiamo usare gli altri due dati,
e ricorrere alle strategie messe a punto per
× e
1/x:
P P 1
D = - => S = - = P · -
S D D
380500 ≤ P ≤ 381500 380500 ≤ P ≤ 381500
=> 1 1 1 =>
146.5 ≤ D ≤ 147.5 ————— ≤ — ≤ —————
147.5 D 146.5
380500 1 381500
=> 2579.6… = —————— ≤ P · — ≤ —————— = 2604.0…
147.5 D 146.5
Concludendo:
2579.6…km2
≤ superficie ≤ 2604.0…km2. In generale:
0 ≤ x1 ≤ x ≤ x2
e => x1/y2 ≤ x/y ≤ x2/y1
0 < y1 ≤ y ≤ y2
Es.: ho
la consegna di tagliare da un pezzo di metallo un cubetto dal
volume di 10 cm3;
è tollerato un errore del 2%, cioè il volume del
cubetto che ottengo può variare in valore assoluto al più
del 2% da 10 cm3;
con che precisione devo realizzare gli spigoli del cubo?
10 cm3
= 10000 mm3;
2% 10000=200;
siano V il volume in mm3
e L lo spigolo in mm; ho V=L3
e L=V1/3;
9800 = 10000–200 ≤ V ≤
10000+200 = 10200 =>
21.3997…= 98001/3
≤ L ≤ 102001/3 = 21.6870…
quindi
devo regolare la macchina con cui tagliare il metallo in modo da
essere sicuro che L sia compreso tra questi due valori.
 Nota.
Se opero sia con dati approssimati che con dati esatti, i
procedimenti visti sopra si semplificano.
Nota.
Se opero sia con dati approssimati che con dati esatti, i
procedimenti visti sopra si semplificano.
Ad
esempio se so che un oggetto ha peso P = 87±1 g, cioè
86g ≤ P ≤ 88g, posso concludere che 6 oggetti uguali ad esso
hanno peso complessivo Q = 6P con 86·6g ≤ Q ≤ 88·6g.
Non è
altro che un caso particolare di:
(0 ≤ x1 ≤ x ≤ x2
e 0 ≤ y1 ≤ y ≤ y2)
=>
x1·y1 ≤ x·y ≤ x2·y2
con y1 = y2 = 6.
 Spesso, quando si ha a che fare con dati
arrotondati, si usano dei procedimenti più
pratici, ma meno rigorosi, usati più
volte anche da noi, in altre voci.
Spesso, quando si ha a che fare con dati
arrotondati, si usano dei procedimenti più
pratici, ma meno rigorosi, usati più
volte anche da noi, in altre voci.
Illustriamoli con alcuni esempi.
 Tre
parti percentuali di un totale, arrotondate, sono: 41.3%, 5.28% e
12.1%. Quanto vale la parte percentuale complessiva?
Tre
parti percentuali di un totale, arrotondate, sono: 41.3%, 5.28% e
12.1%. Quanto vale la parte percentuale complessiva?
41.3 + 5.28 + 12.1 = 58.68, ma non posso dire
che la percentuale complessiva è 58.68%: mentre la seconda
percentuale era arrotondata ai centesimi, la prima e la terza erano
arrotondate ai decimi; non posso quindi ottenere un valore preciso
fino ai centesimi.
Quindi arrotondo il risultato con la
precisione peggiore fra quelle degli addendi, cioè,
in questo caso, ai decimi: 58.68 → 58.7%.
Non posso, però, a rigore, dire che
58.7 è un arrotondamento a 3 cifre significative del
risultato, in quanto questo non sta esattamente tra 58.65% e 58.75%.
Con il procedimento rigoroso avremmo
infatti trovato l'intervallo di indeterminazione:
[41.25+5.275+12.05, 41.35+5.285+12.15] =
[58.575, 58.785]

 Devo eseguire il calcolo tra valori arrotondati: 13.7·0.096/2.45.
Con la CT ottengo: 0.53681633. Ovviamente non ho 8 cifre
significative.
Devo eseguire il calcolo tra valori arrotondati: 13.7·0.096/2.45.
Con la CT ottengo: 0.53681633. Ovviamente non ho 8 cifre
significative.
Allora arrotondo il risultato al numero
di cifre pari al più piccolo tra i numeri di cifre
significative dei vari termini che ho moltiplicato o diviso.
• L'idea è che, nel fare una moltiplicazione o una divisione, l'ordine di grandezza dei fattori determina solo l'ordine di grandezza del risultato mentre il valore delle sue cifre (cioè  la mantissa) dipende solo dalle cifre (cioè dalle mantisse) dei fattori:
la mantissa) dipende solo dalle cifre (cioè dalle mantisse) dei fattori:
35.2·0.02 e 352·2 hanno come risultati 0.704 e 704, che hanno le stesse cifre.
In altre parole il fatto che 3.52 abbia una indeterminazione di 0.01 (arrotondamento ai centesimi: mezzo centesimo in più o in meno) e quello che 352 abbia una indeterminazione di 1 (arrotondamento alle unità: mezza unità in più o in meno) incidono allo stesso modo sulla precisone dei risultati:
quello che conta è l'indeterminazione relativa dei fattori, ossia l'entità della indeterminazione rapportata alla entità del numero: 0.01 su 3.52 equivale a 1 su 352, così come 0.01 su 0.02 equivale a 1 su 2.
Un modo migliore per esprimere la "regola pratica" sarebbe quello di dire che l'indeterminazione relativa del risultato è pari circa alla somma delle indeterminazioni relative dei fattori (o alla indeterminazione maggiore fra le due, quando l'altra è "trascurabile").
Si noti che l'indeterminazione relativa è quella che caratterizza l'accuratezza di una misurazione indipendentemente dall'unità di misura scelta: (44±1) kg equivale a (4400±100) g, e 1/44 equivale a 100/4400.
Nel
nostro caso i tre numeri hanno rispettivamente 3, 2 e 3 cifre
significative; il minimo tra questi è 2; quindi arrotondo il
risultato a 2 cifre: 0.53681633 → 0.54.
Non posso, però, a rigore, dire che
0.54 è un arrotondamento a 2 cifre significative del
risultato, in quanto questo non sta esattamente tra 0.535 e 0.545.
Con il procedimento rigoroso avremmo
infatti trovato l'intervallo di indeterminazione:
[13.65·0.0955/2.455,
13.75·0.0965/2.445] = [0.53098…, 0.54268…]
• Nel caso della moltiplicazione tra i dati arrotondati 3.7 e 0.341 se approssimassi il risultato 1.2617 di 3.7·0.341 a 1.2, l'arrotondamento a 2 cifre (tante quante quelle di 3.7, il dato con approssimazione peggiore), perderei molta informazione; infatti dal calcolo rigoroso dell'intervallo di indeterminazione avrei [3.65·0.3405, 3.75·0.3415] = [1.242825, 1.280625], ossia 1.26 ± 2.
Ciò accade perché il dato approssimato con meno cifre aveva (vedi il precedente "•") una indeterminazione relativa di 1 su 37, mentre arrotondare il risultato a 1.2 sarebbe prendere una indeterminazione di 1 su 12, che è molto peggiore. In tal caso, volendo, possiamo arrotondare a 1.26, che sarebbe come prendere una indeterminazione di 1 su 126.
Entrambe le scelte possono avere delle motivazioni: 1/37 sta tra 1/12 e 1/126.
 L'area
di un quadrato arrotondata a 3 cifre è 3680cm2.
Voglio trovare la misura del lato. Facendo la radice quadrata con la
CT ottengo: 60.663004, ma non posso dire che questa è la
misura del lato in cm.
L'area
di un quadrato arrotondata a 3 cifre è 3680cm2.
Voglio trovare la misura del lato. Facendo la radice quadrata con la
CT ottengo: 60.663004, ma non posso dire che questa è la
misura del lato in cm.
Allora arrotondo il risultato a tante
cifre quante erano le cifre significative del valore di partenza.
Nel nostro caso il valore iniziale aveva 3 cifre significative,
quindi: 60.663004 → 60.7.
Non posso, però, a rigore, dire che
60.7 è un arrotondamento a 3 cifre significative del
risultato, in quanto questo non sta esattamente tra 60.65 e 60.75.
Infatti con il procedimento rigoroso
avremmo trovato l'intervallo di indeterminazione:
[√3675, √3685 ] = [60.6217…, 60.7042…]
 Nota 1. Prima di eseguire
calcoli approssimati, conviene verificare se è possibile
eseguire trasformazioni algebriche che
semplifichino i calcoli:
Nota 1. Prima di eseguire
calcoli approssimati, conviene verificare se è possibile
eseguire trasformazioni algebriche che
semplifichino i calcoli:
per calcolare 2.666…·0.111…/4 invece di operare usando approssimazioni
di 2.666… e 0.111… si può osservare che il primo termine è uguale
a 2 e 2/3, ossia 8/3, e che il secondo è uguale a 1/9, e trasformare
2.666…·0.111… in 8·1/(3·9) = 8/27, e fare 8/27/4 → 2/27
(→ 0.074074074…).
Può essere utile (per economizzare spazio, ricordare più
facilmente i valori, posticipare il problema di come approssimare, …) conservare il più
a lungo possibile rappresentazioni esatte dei risultati:
cacolando direttamente √15 / 2 / √5 ottengo 0.8660254, trasformandolo in
√(15/5)/2 e poi in √3/2 esprimo in forma più compatta
il risultato.
Se si deve calcolare il valore approssimato di un termine che
contiene più di due numeri conviene calcolare i valori intermedi senza
arrotondamenti e arrotondare solo il risultato finale, per evitare di accumulare troppi
errori di arrotondamento:
se si vogliono esprimere delle parti di un totale pari a 280 in 360-esimi per poterle
rappresentare su un diagramma a settori circolari possiamo moltiplicare ogni dato per il
fattore di proporzionalità k=360/280 (che posso calcolare una volta per tutte e
memorizzare nella CT). Se un dato è 192 gli viene associato il settore ampio
192·k° = 246.86…°, che posso arrotondare a 247°; se invece avessi
prima arrotondato k = 360/280 = 1.285… a 1.29 e avessi moltiplicato i dati per questo
valore avrei ottenuto nel caso del nostro dato 192·1.29 = 247.68… ottenendo
l'arrotondamento 248°.
Se si deve calcolare il valore di un termine che contiene
più numeri noti solo in modo approssimato si possono comporre i procedimenti (o le
"regole pratiche") relativi alle varie operazioni che intervengono in esso.
Qui vedi come puoi effettuare questi calcoli con R.
In particolare è illustrato il calcolo del volume di un parallelepipedo
aventi dimensioni troncate ai millimetri 3.1, 4.6 e 5.4; si ottiene che il volume
(in cm3) cade in [77.004, 82.27], intervallo ampio 5.716; possiamo
prendere: volume = 80±3 cm3.
 Nota 2. Il simbolo di
eguaglianza "=", oltre che per indicare
Nota 2. Il simbolo di
eguaglianza "=", oltre che per indicare  equazioni in senso stretto (e
equazioni in senso stretto (e  assegnazioni o
assegnazioni o  sostituzioni),
viene usato anche per indicare equazioni che sono vere solo
in senso approssimato.
sostituzioni),
viene usato anche per indicare equazioni che sono vere solo
in senso approssimato.
Ad esempio scrivendo 20/3=6.67 intendiamo
dire che 20/3 ha come valore arrotondato 6.67, non che vale
esattamente 6.67, cioè che 20/3 = 6.67000….
In questi casi al posto di "="
si può usare "≈" o "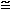 "
(che si legge "è approssimativamente uguale a"). Ma
questo simbolo è usato anche quando non si sa stimare la
precisione dell'approssimazione; ad esempio se scrivo:
popolazione ≈ 1.5
milioni non intendo necessariamente dire che 1.5 milioni è un
arrotondamento del valore della popolazione, ma che la popolazione è
"circa" 1.5 milioni (potrebbe anche essere, ad es., più
di 1.6 milioni).
"
(che si legge "è approssimativamente uguale a"). Ma
questo simbolo è usato anche quando non si sa stimare la
precisione dell'approssimazione; ad esempio se scrivo:
popolazione ≈ 1.5
milioni non intendo necessariamente dire che 1.5 milioni è un
arrotondamento del valore della popolazione, ma che la popolazione è
"circa" 1.5 milioni (potrebbe anche essere, ad es., più
di 1.6 milioni).
Si usano anche notazioni come: x=3.2±0.1.
Ciò non significa "x=3.2+0.1 o x=3.2–0.1":
come abbiamo visto, si tratta di un'abbreviazione per:
3.2–0.1≤x≤3.2+0.1.
Notiamo, ancora, che se per la misura di
due grandezze dispongo delle seguenti approssimazioni: x=3.2±0.1
e y=3.3±0.1, non posso concludere che le grandezze sono
diverse. Potrebbero essere uguali in quanto gli intervalli
[3.2–0.1,3.2+0.1] = [3.1,3.3] e [3.3–0.1,3.3+0.1] =
[3.2,3.4] non sono separati ma hanno l'intervallo [3.2,3.3] in
comune.
Per fare un altro esempio, se vogliamo verificare
"sperimentalmente"  il teorema di Pitagora, misurati a, b e c, non possiamo trovare che esattamente a2+b2=c2, ma dobbiamo accontentarci che gli esiti delle misurazioni non contraddicano il teorema, nel senso che gli intervalli di indeterminazione di a2+b2 e di c2 abbiano un intervallo in comune.
il teorema di Pitagora, misurati a, b e c, non possiamo trovare che esattamente a2+b2=c2, ma dobbiamo accontentarci che gli esiti delle misurazioni non contraddicano il teorema, nel senso che gli intervalli di indeterminazione di a2+b2 e di c2 abbiano un intervallo in comune.
 Nota 3. Per
aumentare la precisone degli strumenti misuratori di lunghezze spesso si usa
il nonio. Vedi
Nota 3. Per
aumentare la precisone degli strumenti misuratori di lunghezze spesso si usa
il nonio. Vedi  .
.
 Nota 4.
Come si è visto, per calcolare quanto vale F(h) se conosco h in modo approssimato, ad esempio se so che
h1 ≤ h ≤ h2, e se so che F cresce in tale intervallo,
posso approssimare F(h) con [F(h1), F(h2)]; se so
che F decresce posso approssimare F(h) con [F(h2), F(h1)]. Invece,
per calcolare in modo approssimato F(h) quando h varia un un intervallo in cui F non è
crescente o decrescente, devo tener conto dell'andamento della funzione. Vedi il seguente
Nota 4.
Come si è visto, per calcolare quanto vale F(h) se conosco h in modo approssimato, ad esempio se so che
h1 ≤ h ≤ h2, e se so che F cresce in tale intervallo,
posso approssimare F(h) con [F(h1), F(h2)]; se so
che F decresce posso approssimare F(h) con [F(h2), F(h1)]. Invece,
per calcolare in modo approssimato F(h) quando h varia un un intervallo in cui F non è
crescente o decrescente, devo tener conto dell'andamento della funzione. Vedi il seguente  esercizio 3.4.
esercizio 3.4.
 Nota 5.
A volte viene usato il termine tolleranza per indicare la
precisione con cui è stata effettuata una certa operazione fisica
(ad es. un taglio effettuato o il peso di un oggetto).
Nota 5.
A volte viene usato il termine tolleranza per indicare la
precisione con cui è stata effettuata una certa operazione fisica
(ad es. un taglio effettuato o il peso di un oggetto).
 Nota 6.
Quando il termine è complesso e compaiono diverse variabili può essere comodo ricorrere
al generatore di numeri casuali: vedi qui, in fondo.
Nota 6.
Quando il termine è complesso e compaiono diverse variabili può essere comodo ricorrere
al generatore di numeri casuali: vedi qui, in fondo.
Esercizi: 


 altri collegamenti [nuova pagina]
altri collegamenti [nuova pagina]

 Spesso
di un numero reale X non conosciamo tutte le cifre, ma solo
un'approssimazione per difetto e un'approssimazione per eccesso. Ciò
può accedere, ad esempio, se X è la
Spesso
di un numero reale X non conosciamo tutte le cifre, ma solo
un'approssimazione per difetto e un'approssimazione per eccesso. Ciò
può accedere, ad esempio, se X è la  misura di
una grandezza fisica ottenuta attraverso la lettura di uno strumento
di misurazione
o se X è stato precedentemente sottoposto a un
misura di
una grandezza fisica ottenuta attraverso la lettura di uno strumento
di misurazione
o se X è stato precedentemente sottoposto a un  arrotondamento
e noi non conosciamo il valore originale.
arrotondamento
e noi non conosciamo il valore originale.




 x1 ≤ x ≤ x2
e => x1+y1 ≤ x+y ≤ x2+y2
y1 ≤ y ≤ y2
x1 ≤ x ≤ x2
e => x1+y1 ≤ x+y ≤ x2+y2
y1 ≤ y ≤ y2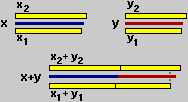
 0 ≤ x1 ≤ x ≤ x2
e => x1·y1 ≤ x·y ≤ x2·y2
0 ≤ y1 ≤ y ≤ y2
0 ≤ x1 ≤ x ≤ x2
e => x1·y1 ≤ x·y ≤ x2·y2
0 ≤ y1 ≤ y ≤ y2

 somma] e dividere equivale a
moltiplicare per il reciproco [
somma] e dividere equivale a
moltiplicare per il reciproco [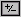 x1 ≤ x ≤ x2 => - x2 ≤ -x ≤ -x1
x1 ≤ x ≤ x2 => - x2 ≤ -x ≤ -x1
 Es.: La
temperatura in °C nella località W in un certo giorno
ha avuto come valore minimo m=12 e come valore massimo
M=24. Sapendo
che queste misure hanno la precisione di 1°, come possiamo
approssimare l'escursione termica, cioè M–m?
Dobbiamo calcolare M–m, cioè M+(–m).
Es.: La
temperatura in °C nella località W in un certo giorno
ha avuto come valore minimo m=12 e come valore massimo
M=24. Sapendo
che queste misure hanno la precisione di 1°, come possiamo
approssimare l'escursione termica, cioè M–m?
Dobbiamo calcolare M–m, cioè M+(–m).

 Es.: In una
pubblicazione dell'ISTAT si trova che il Lussemburgo, nel 1990, aveva
popolazione P di 381 mila abitanti, densità D di 147 ab./km2
e superficie S di 3 mila km2.
Per trovare con più precisione la superficie possiamo usare gli altri due dati,
e ricorrere alle strategie messe a punto per
× e
1/x:
Es.: In una
pubblicazione dell'ISTAT si trova che il Lussemburgo, nel 1990, aveva
popolazione P di 381 mila abitanti, densità D di 147 ab./km2
e superficie S di 3 mila km2.
Per trovare con più precisione la superficie possiamo usare gli altri due dati,
e ricorrere alle strategie messe a punto per
× e
1/x:
 Nel caso di queste funzioni e, più in generale, della funzione
Nel caso di queste funzioni e, più in generale, della funzione  xa
xa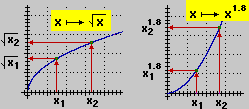
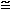 "
"
