Da Galileo alla derivazione

    Nel momento in cui si introduce la derivazione è opportuno fare anche qualche richiamo storico a quando, e come, sono state sviluppate le idee ad essa relative, segnando il momento più significativo nello sviluppo della storia della matematica.  Nel punto (1) è richiamato un piccolo brano della storia della Fisica di Bernal.  Nel punto (2) è presentato un piccolo esempio per illustrare il livello di matematizzazione che si potrebbe raggiungere in una scuola non a indirizzo scientifico.  Gli esempi nei punti (3) e (4) danno un'idea del livello ulteriore raggiungibile in scuole ad indirizzo scientifico.

(1)  Lo studio dei movimenti e dei fattori fisici che li governano è affrontato da un ramo della fisica chiamato dinamica (nome derivato dal greco dinamis, forza);  è una branca della meccanica (che si occupa del funzionamento dei meccanismi; di quello dei motori si occupano altri rami della fisica, come l'elettromagnetismo – motori elettrici - e la termodinamica – motori a carburante).  I personaggi che, più di ogni altro, sono all'origine dello sviluppo della dinamica sono l'italiano Galileo Galilei (1564-1642), i francesi René Descartes (1596-1650), spesso italianizzato in "Cartesio", e Pierre de Fermat (1601-1665), l'inglese Isaac Newton (1643-1727).
    Galileo formulò il principio d'inerzia, secondo il quale un corpo cambia velocità solo se su di esso agisce una forza ("inerzia" indica lo stato di chi non modifica il proprio comportamento).  Prima di lui, ingannati dal fatto che un oggetto in movimento tende a fermarsi se non viene continuamente spinto o tirato, si riteneva che per mantenere un corpo in movimento occorresse esercitare su di esso una forza.  Galileo intuì che, invece, era il rallentamento del corpo ad essere causato dall'intervento di forze (attrito, resistenza dell'aria, …), e confermò questa sua tesi analizzando matematicamente gli esiti di una serie di esperimenti in cui cercò di ridurre l'incidenza delle forze frenanti.  Galileo mise a punto anche un modello matematico per il movimento dei corpi che cadono.  La novità introdotta da Galileo fu proprio lo studio dei fenomeni attraverso gli esperimenti e la loro rappresentazione mediante leggi matematiche generali, rompendo con la tradizione aristotelica, secondo la quale i fenomeni erano studiati su una base teologica e filosofica (e aprendo collegamenti tra la "scienza" e la "tecnica", che fino ad allora elaborava le proprie conoscenze su base empirica).  Vedi "Storia della Fisica" di Jhon D. Bernal.
    Un ruolo fondamentale per i successivi sviluppi lo ha avuto la matematizzazione del concetto di spazio mediante le coordinate, con la conseguente possibilità di descrivere curve mediante equazioni.  Questa rappresentazione numerica dello spazio è dovuta a Descartes, dal cui nome deriva la parola "coordinate cartesiane", e a Fermat, a cui si devono anche le prime formulazioni del rapporto incrementale.
    Newton mise, infine, a punto un modello matematico generale dell'origine dei movimenti introducendo il concetto di derivata per descrivere matematicamente la velocità (come derivata dello spostamento) e la accelerazione (come derivata della velocità):

un corpo soggetto complessivamente a una forza F si muove con una accelerazione avente la stessa direzione di F e intensità proporzionale all'intensità di F e alla propria massa.

    In seguito al principio formulato da Newton, il concetto di forza è stato precisato ed espresso come prodotto m·a tra l'accelerazione a che essa è in grado di imprimere ad un corpo e la massa m di esso.  E ha preso il nome Newton (N) la sua unità di misura:   1 N = 1 kg·m/s².  Accanto a Newton, lo sviluppo del concetto di derivata è dovuto a Leibniz.

Galilei su WolframAlpha,  su Wiki,    Newton su WolframAlpha,  su Wiki,  Newton's laws su WolframAlpha,   Leibniz su WolframAlpha,  su Wiki,    notazioni

(2)  Prendiamo in esame il lancio di un oggetto. Consideriamo una freccia o una bilia metallica, in modo che sia trascurabile l'attrito con l'aria. Supponiamo di lanciarla con una inclinazione di 45°, con una velocità tale che avanzi di 35 m/s e si innalzi di 35 m/s, ossia che che si muova nella direzione 45° con la velocità di √(35²+35²) m/s = 49.50 m/s (approssimando al cm/s).  Se non ci fosse la forza di gravitazione che attira l'oggetto verso terra (peso), esso continuerebbe a procedere nella direzione 45°, con la stessa velocità. La presenza della forza peso, diretta verticalmente verso il basso, frena la salita, ma non ostacola l'avanzamento orizzontale, come si vede nella figura sottostante, in cui si è preso l'asse x diretto come l'avanzamento orizzontale: ad ogni secondo la x dell'oggetto aumenta di 35 (dopo 7 s è avanzato di 7·35 = 49·5 = 490/2 = 245 m).

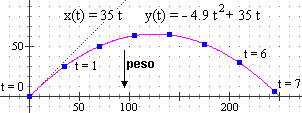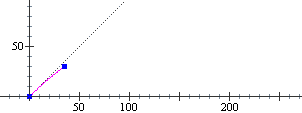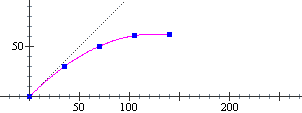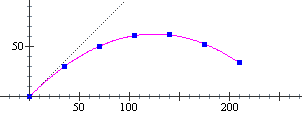
    Mentre il vettore velocità dell'oggetto è man mano diretto tangenzialmente alla traiettoria, l'accelerazione in questo caso è sempre diretta verticalmente e verso il basso; ciò è la traduzione di quanto detto sopra: l'oggetto avanza orizontalmente con la stessa velocità ma si alza con velocità man mano minore, fino a diventare nulla quando l'oggetto raggiunge la massima altezza, dopo di che la velocità verticale cambia direzione, e l'oggetto incomincia a scendere.
    L'accelerazione in questo caso è quella di gravità, che alla nostra latitudine, al livello del mare, è 9.80±0.01 m/s². È facile dedurre che il moto del nostro oggetto è descritto dalle equazioni riportate in figura, cioè (considerndo x e y in metri e t in secondi) da:  x = 35 t, y = – 4.9 t² + 35 t.
    Infatti il vettore velocità (in m/s) è:
        (x'(t), y'(t))  =   (35, – 4.9·2 t^{2 – 1} + 35)  =   (35, – 9.8 t + 35)
la cui velocità di variazione, ossia il vettore accelerazione (in m/s²), è:
        ( D_t(35), D_t(–9.8 t + 35) )  =  (0, –9.8)
che ha come intensità 9.8 m/s² e direzione verticale in basso (la componente orizzontale è 0 e quella verticale è negativa): è proprio l'accelerazione di gravità.
    La traiettoria dell'oggetto lanciato è una parabola, infatti da  x = 35 t AND y = – 4.9 t² + 35 t  si ricava t = x/35 e, quindi, y = – 4.9 (x/35)² + 35x/35, ossia y = –0.004x²+x.  E il "proiettile" arriva nel punto x (diverso da 0) in cui y = 0, ossia quando –0.004x²+x = (–0.004x+1)x = 0, cioè quando x = 1/0.004 = 1000/4 = 250 (metri), come si vede anche dalla figura.

Per approfondimenti sui possibili intrecci tra matematica e fisica  vedi qui.

(3)  Vediamo come si può determinare il vettore velocità nel caso del moto curvilineo seguente, che a lato è rappresentato in forma animata per t (inteso qui come tempo in secondi) che varia da 0 a 4 (si tratta di istantanee scattate ogni 1/2 secondo):           x(t) = t2 – 5t + 5,     y(t) = t2 – 3.     Dalla animazione capiamo che il mezzo rallenta entrando nella curva (i pallini si avvicinano) e poi accelera (i pallinini si diradano). •  Per trovare la direzione della velocità basta fare: dy/dt = 2·t, dx/dt = 2·t−5, dy/dx = 2t/(2t–5) •  Le velocità in orizzontale e in verticale non sono altro che le derivate x'(t) e y'(t) di x e di y rispetto a t, per cui il vettore velocità è (2t–5, 2t). Il vettore accelerazione è dunque:  (Dt(2t–5), Dt(2t)) = (2, 2)  (2 m/s2 sia in direzione x che in direzione y, ossia inclinazione di 45° rispetto asse x e intensità √(22+22) = √(2·22) = 2√2 m/s2).  Anche in questo caso il corpo è soggetto a una accelerazione costante, diretta non verticalmente ma inclinata di 45°. In altre parole il corpo in movimento è soggetto a una forza costante diretta come indicato nella figura qui a destra.     Possiamo anche concludere che la traiettoria è una parabola con asse di simmetria inclinato di 45°.     Qual è il vertice di essa? È il punto in cui la tangente è perpendicolare all'asse di simmetria. L'asse ha pendenza 2/2 = 1. La tangente ha la pendenza del vettore velocità, (2t)/(2t–5). Dobbiamo trovare per quale t essa e la pendenza dell'asse sono una il reciproco dell'altra cambiato di segno:       (2t–5)/(2t) = –1  <=>  2t–5 = –2t  <=>  4t = 5  <=>  t = 5/4     Si tratta quindi del punto:  x = (5/4)2–5·5/4+5 = 5/16 = 0.3125,  y = (5/4)2–3 = –23/16 = –1.4375.

(4)  Consideriamo, infine, un mezzo che si muove lungo una traiettoria circolare.

Nella figura più a sinistra è illustrato il caso di un mezzo che si muove con velocità di intensità costante: il vettore velocità cambia direzione ma ha sempre la stessa lunghezza. È come il moto di un satellite in orbita circolare attorno alla Terra. La sua accelerazione è diretta come la forza che lo attira verso la Terra.     Nel caso raffigurato a destra invece il mezzo si muove con velocità di intensità crescente. Potrebbe essere un'automobilina telecomandata legata ad un filo fissato al terreno: la forza impressa dal motorino la fa andare via via più velocemente, la forza esercitata dal filo le impedisce di proseguire lungo una retta. La prima forza è diretta tangenzialmente, la seconda verso il centro di rotazione; la loro somma è una forza che punta un po' più avanti del centro di rotazione. Il vettore accelerazione, rappresentato in figura, è diretto come questa forza; sono raffigurate anche le sue componenti tangenziale e centrale, corrispondenti alle due componenti della forza.