Dipendenza e indipendenza

  Qual è la probabilità che alzando 2 volte un mazzo (nuovo) di carte da scopa ottenga sempre una carta di denari? Qual è la probabilità che estraendo 2 carte dal mazzo queste siano entrambe di denari?

•  Nel caso della alzata, avendo supposto il mazzo nuovo (e non truccato e mescolato bene) posso ritenere che, tagliandolo, le carte compaiano con distribuzione uniforme. Quindi [] posso fare: Probabilità = NumeroCasiFavorevoli / NumeroCasiPossibili     I casi possibili sono 40·40: 40 carte possibili per la prima alzata e 40 per la seconda.     I casi favorevoli sono 10·10: sono 10 le carte di denari.     La probabilità che esca una carta di denari entrambe le volte è: (10·10)/(40·40) = 1/16 = 6.25%		40     40     10     10
–  Posso anche considerare direttamente la variabile casuale "seme", a valori in {, , , }, che, per gli stessi motivi di prima, posso ritenere con distribuzione uniforme: l'uscita di una carta di denari ha la stessa probabilità di quella di una di fiori o … Quindi posso usare: Probabilità = NumeroCasiFavorevoli / NumeroCasiPossibili.     I casi possibili sono 4·4 (4 semi possibili), quelli favorevoli 1·1 (1 è il seme che mi interessa).     La probabilità cercata dunque è: (1·1)/(4·4) = 1/16 = 6.25%		4      4      1      1

–  Avrei anche potuto utilizzare un 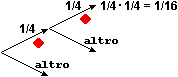grafo ad albero: •  rappresento con successive diramazioni i diversi esiti possibili per la prima alzata e per la seconda (eventualmente raggruppando gli esiti "sfavorevoli" in un'unica diramazione); •  associo agli archi che corrispondono a esiti "favorevoli" la relativa probabilità; •  calcolo, per ogni percorso (dal nodo iniziale a un nodo finale) costituito solo da archi "favorevoli", il prodotto delle probabilità associate ai vari archi e lo scrivo a fianco del nodo finale; •  sommo i valori così calcolati (in questo caso non devo fare somme perché c'è solo un percorso)

Perché faccio il prodotto?  La cosa è facilmente comprensibile se ragioniamo in termini di frequenza percentuale: se tra gli abitanti di in un certo paese le donne sono il 51% e tra le donne quelle con più di 60 anni sono il 35%, per trovare il numero delle donne con più di 60 anni moltiplico il numero degli abitanti per 51% e poi per 35%, ossia la loro percentuale rispetto al totale degli abitanti è 51% · 35% = 0.51·0.35 = 0.18 = 18%.

•  Anche nel caso della estrazione posso ritenere equiprobabili le carte del mazzo.     I casi possibili sono 40·39 (alla seconda estrazione dispongo di una carta in meno) [sono le disposizioni di 40 oggetti 2 a 2]     I casi favorevoli sono 10·9 (se nella prima estrazione è uscito denari, nel mazzo sono rimaste 9 carte di denari).

40     39     10      9

La probabilità cercata è:  (10·9)/(40·39) = 9/4/39 = 5.8% (arrotondamento)  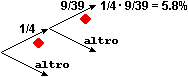  Anche in questo caso sarei potuto ricorrere a un grafo ad albero.

•  Un ulteriore esempio:  qual è la probabilità che lanciando due dadi equi si ottengano uscite U1 e U2 con somma pari?  Se P e D sono gli insiemi dei numeri pari e dei numeri dispari, devo determinare Pr(U1+U2P). Con un grafo posso procedere così:
dopo aver osservato che Pr(U1P) = Pr(U2P) = Pr(U1D) = Pr(U2D) = 1/2 posso (1) rappresentare con successive diramazioni i diversi esiti possibili ("pari" e "dispari") per U1 e per U2, poi (2) associare ad ogni arco la corrispondete probabilità, quindi (3) calcolare per ogni nodo finale il prodotto dei valori associati agli archi che si percorrono per arrivare ad esso dal nodo iniziale; infine (4) sommo i valori dei nodi finali corrispondenti ai percorsi che individuano i casi "favorevoli" (U1 e U2 entrambe pari o entrambe dispari), e ottengo che il valore cercato è 1/2.

Con le "caselle" avrei potuto procedere così:  i casi possibili sono 6·6;  i casi favorevoli sono 6·3 (nella seconda estrazione ho 3 possibilità di ottenere una uscita della stessa "parità" della prima);  quindi la probabilità cercata è: 6·3/(6·6) = 1/2

6     6     6      3

Esercizio:   testo e soluzione

   Riesaminiamo i due esempi iniziali. Indichiamo con la variabile casuale S₁ il seme della prima uscita (alzata o estrazione) e con la variabile casuale S₂ quello della seconda uscita.

    Nel caso della alzata le variabili casuali S₁ e S₂ sono indipendenti: qualunque seme abbia la 1^a carta, la probabilità che la 2^a abbia un certo seme è sempre la stessa.
    Ciò corrisponde al fatto che il grafo relativo all'alzata si riproduce allo stesso modo passando da una diramazione alla successiva.
    Per calcolare Pr(S₁ = AND S₂ = ) posso fare direttamente Pr(S₁ = )·Pr(S₂ = ) = 1/4·1/4 = 1/16

    Nel caso della estrazione le variabili casuali S₁ e S₂ non sono indipendenti: ad es. Pr(S₂ = ) (la probabilità che la 2^a carta sia di ) dipende dal valore assunto da S₁ (cioè dal seme della 1^a carta).
    Ciò corrisponde al fatto che il grafo relativo alla estrazione non si riproduce allo stesso modo passando da una diramazione alla successiva: al primo arco "" è associata la probabilità 1/4, al secondo arco "" è associata la probabilità 9/39.

    In generale, due eventi A e B vengono detti indipendenti se:   Pr(A AND B) = Pr(A)·Pr(B)
    Se, invece, l'ipotesi che un evento si verifichi modifica la valutazione che l'altro possa verificarsi (cioè se i due eventi non sono indipendenti) diciamo che gli eventi sono dipendenti:
sapere che alla 1^a estrazione è uscito denari cambia le mie aspettative sull'uscita di denari alla 2^a (esse si riducono): "uscire denari alla 1^a estrazione" e "uscire denari alla 2^a estrazione" sono eventi dipendenti.

    Due variabili casuali X e Y sono indipendenti se sono indipendenti gli eventi A e B comunque prenda A evento relativo a X (condizione in cui compare solo la variabile X) e B evento relativo a Y (condizione in cui compare solo variabile Y): conoscere qualcosa su come si manifesta X non modifica le mie aspettattive sui modi in cui può manifestarsi Y, e viceversa. Altrimenti sono dipendenti.
Sapere qualcosa a proposito del seme della 1^a carta estratta cambia le mie valutazioni sul seme che potrebbe avere la 2^a carta estratta: il seme della 1^a estrazione e quello della 2^a sono variabili casuali dipendenti.

  Nota.  Il concetto di dipendenza ora introdotto è diverso da quello impiegato per esprimere il legame tra due grandezze quando una varia in funzione dell'altra.
    Se A e L sono area e lato di un generico quadrato, A dipende da L nel senso che ad ogni valore di L corrisponde un unico valore di A. Invece nel caso dell'estrazione dire che le variabili S₁ e S₂ sono dipendenti non significa che l'una è funzione dell'altra: l'uscita di alla 1^a estrazione non determina univocamente l'uscita della 2^a estrazione.
    Quando è il caso, per distinguere i due tipi di dipendenza, si parla, rispettivamente, di dipendenza funzionale (o deterministica) e di dipendenza probabilistica.

  Facendo riferimento a un esempio considerato alla voce calcolo delle probabilità, supponiamo di voler trovare la probabilità che un alunno insufficiente in matematica sia insufficiente anche in fisica, valore che indichiamo con l'espressione:   Pr(S∈F | S∈M) (leggendo: «probabilità dell'evento S∈F nella condizione che si verifichi l'evento S∈M»).

La popolazione a cui riferire l'essere insufficiente in fisica non è il totale degli alunni, ma solo il sottoinsieme di quelli insufficienti in matematica.     La probabilità cercata è dunque uguale a:
Pr(S∈F AND S∈M) ———————————————— = 28%/42% = 67% Pr(S∈M)
–   Per calcolare Pr(S2= AND S1=) nel caso della estrazione ho fatto: Pr(S2= AND S1=)  =  Pr(S1=) · Pr(S2= | S1=)  = 1/4 · 9/39
[ Pr(S2= | S1=): probabilità che la seconda estratta sia   nota l'informazione che la prima estratta è stata  ]

  Il concetto di probabilità condizionata introdotto nei due esempi precedenti può essere generalizzato.

            Pr(A AND B)
  Pr(A|B) = ———————————
               Pr(B)

 Pr(A AND B) = Pr(B)·Pr(A|B)

    Nel caso in cui A e B sono indipendenti, ovviamente le formule diventano  Pr(A|B) = Pr(A) [il verificarsi o meno di B non condiziona la valutazione di Pr(A)] e   Pr(B AND A) = Pr(B)·Pr(A).

  Un certo test sanitario per valutare la presenza (esito positivo) o assenza (esito negativo) della malattia X ha attendibilità del 95% (in caso di presenza c'è il 95% di probabilità che l'esito sia positivo , in caso di assenza il 95% di probabilità che sia negativo). Si sa da statistiche serie che l'1% della popolazione è affetta dalla malattia X. Se per una persona il test dà esito positivo, qual è la probabilità che essa sia realmente malata?

Devo determinare Pr("essere malato" | "risultare positivo"): Pr("essere malato" AND "risultare positivo") ———————————————————————————————————————————— Pr("risultare positivo")

Per calcolare il rapporto devo trovare il valore dei "?" della seguente tabella a 2 entrate (il valore di ogni casella dipende da due input: la condizione rispetto al test - riga - e quella rispetto alla malattia - colonna):
metto i dati sulla popolazione (prime 2 colonne dell'ultima riga), poi utilizzo il dato sull'attendibilità del test (per ottenere le prime 2 colonne della 1ª riga: 1·95%=0.95, 99·5%=4.95), infine completo la 1ª riga: 0.95+4.95=5.90).

	malati	sani	totale		malati	sani	totale		malati	sani	totale
positivi	?   ?       1 99 100				0.95 4.95 ?       1 99 100				0.95 4.95 5.90       1 99 100
negativi
totale

La probabilità cercata è dunque 0.95% / 5.90% = 16%, molto meno di 95%, come si sarebbe potuto pensare.     In alternativa all'uso della tabella, per trovare Pr("risultare positivo") potevo usare un grafo ad albero, come si è fatto a lato.

    Questo esempio evidenzia il ruolo del calcolo delle probabilità nella razionalizzazione delle situazioni "incerte".
    Esso non è tuttavia sempre sufficiente: si pensi ai vaccini, che a volte hanno una certa probabilità di causare l'insorgere delle malattie stesse; per decidere se rendere obbligatoria una vaccinazione non basta trovare che tale probabilità è bassa rispetto alla diffusione della malattia: imporre a chi potrebbe rimanere sano una vaccinazione che può causare una malattia comporta valutazioni anche di tipo morale.
    Vi sono anche casi in cui si ricorre a valutazioni probabilistiche erronee perché basate su campioni mal scelti o per altri difetti metodologici:  tipico è l'esempio di un sondaggio telefonico che può avere come risposta A o B in cui si tenga conto solo di chi accetta di rispondere senza considerare il fatto che coloro che non vogliono rispondere potrebbero, per la natura della questione, essere più inclini a una delle due risposte.
    E vi sono casi in cui se ne fa un uso improprio, ad es. quando si confonde la presenza di una relazione di dipendenza probabilistica con la presenza di un legame di causa-effetto:  se X è una certa malattia o un certo comportamento, il fatto che esso si riscontri più facilmente tra familiari, più precisamente il fatto che Pr("avere X" | "avere genitori o fratelli con X") > Pr("avere X" | NOT "avere genitori o fratelli con X"), non permette di concludere che all'origine di X vi siano essenzialmente fattori genetici; infatti i fattori principali potrebbero essere di tipo ambientale o sociale, e la relazione probabilistica trovata potrebbe essere dovuta al fatto che è più facile condividere usi, costumi e ambienti con un familiare che con un estraneo.

  Un po' di parole:
•  Qual è la probabilità che estraendo 2 carte da un mazzo da 40 esca esattamente una carta di denari, cioè, usando le notazioni introdotte in precedenza, quanto vale Pr(S₁ = XOR S₂ = )?
    Facendo riferimento al grafo considerato in precedenza osservo che vi sono due percorsi possibili: -"altro" e "altro"-; il primo percorso ha probabilità 1/4·30/39, il secondo 3/4·10/39; in tutto, quindi: 1/4·30/39 + 3/4·10/39 (= 15/39 = 38.46%).
    Il procedimento qui esemplificato, analogo a quello usato anche nell'esempio dei dadi e nell'esempio precedente, per trovare Pr("risultare positivo"), è descrivibile a parole con "sommare le probabilità corrispondenti a tutti i percorsi che danno luogo all'evento di cui si vuole valutare la probabilità". Qualcuno lo riassume con una formula (che non riportiamo) detta della probabilità totale.
•  Anche l'intero procedimento esemplificato nel punto precedente (probabilità di essere … nell'ipotesi che il test abbia dato risposta …) può essere sintetizzato con una formula (che non riportiamo) detta di Bayes o delle ipotesi. Per i casi più semplici è sufficiente (e sicuramente più semplice e "controllabile") procedere in modo esteso usando una tabella o un grafo come si è fatto qui.
•  La schematizzazione mediante grafi ad albero (associare ad ogni diramazione un evento e la relativa probabilità) si può usare quando gli eventi associati agli archi di una diramazione ("l'uscita è pari" e "l'uscita è dispari" nell'esempio dei dadi) costituiscono un gruppo completo di eventi (cioè almeno uno di essi deve accadere) incompatibili (nessuno di essi può accadere contemporaneamente ad un altro). 
    Il ragionamento raffigurato con le "caselle" (rapporto tra "casi favorevoli" e "casi possibili") si può usare solo quando i casi possibili siano un gruppo completo di eventi incompatibili e anche equiprobabili.
•  Due parole che si incontrano spesso affrontando esercizi di calcolo delle probabilità sono reintroduzione e rimpiazzamento. La loro spiegazione è semplice. Quando si prende ripetutamente un oggetto da un certo insieme di oggetti si dice che lo si fa con reintroduzione o con reinserimento o con rimpiazzamento se, dopo ogni presa, l'oggetto pescato viene poi reinserito nell'insieme degli oggetti (in inglese si usano le espressioni with/without replacement per con/senza rimpiazzamento). Tornando all'esempio iniziale delle carte, l'alzata è effettuata con rimpiazzamento, l'estrazione senza.

Esercizi: e

 altri collegamenti     [nuova pagina]