Strutture numeriche e non

  In varie voci precedenti abbiamo visto che non solo sui numeri si possono eseguire operazioni che danno luogo ad altri numeri, ma vi sono altri oggetti matematici su cui si possono eseguire operazioni che danno luogo ad oggetti dello stesso tipo: vettori, funzioni (e in particolare funzioni polinomiali e trasformazioni geometriche), condizioni, stringhe, …. Viene allora naturale mettere a fuoco le analogie che vi sono tra il modo di operare con questi oggetti e il modo di operare con i numeri. A questo scopo si possono generalizzare concetti già introdotti per gli insiemi numerici come quello di formula (considerando anche variabili, costanti e termini che rappresentano oggetti non numerici e simboli di operazioni e di relazioni tra oggetti non numerici - ne vedremo molti esempi in questa voce) e quello di struttura.
    Un insieme può essere considerato una struttura se si fissano una o più operazioni, cioè funzioni che hanno input e output in esso. Si dice che un suo sottoinsieme è una sottostruttura rispetto alle operazioni fissate se è chiuso rispetto ad esse. Un insieme A può essere considerato una struttura non solo stabilendo un modo per operare sui suoi elementi (cioè definendo un'operazione), ma anche determinando un modo per confrontarli, cioè definendo una relazione, come "≤" nel caso dei numeri.

x   y  a a a b a c b b b c c c				Nota 1. Come ho generalizzato il concetto di funzione ai casi non numerici così posso passare dalle relazioni numeriche [ funzione 1] a quelle tra altri tipi di oggetti. Ad es. la relazione di ordine alfabetico "≤" tra l'insieme A delle lettere {a, b, c} è una relazione a 2 posti su A. È l'insieme delle coppie (Lettera1, Lettera2) con Lettera1 che precede o coincide con Lettera2; può essere rappresentata elencando le coppie in una tabella, se esse sono in quantità finita, come in questo caso. Oppure evidenziando le coppie che la verificano su una specie di piano cartesiano (vedi figura a sinistra). Oppure può essere descritta come una funzione a 2 input in A e 1 output in {V, F}: alla coppia (x, y) viene associato V se x è in relazione con y, viene associato F altrimenti: vedi figura a destra.  Analogamente, una relazione a 3 posti su un insieme A può essere descritta come una funzione a 3 input in A e 1 output in {V, F}. E così via. [ operatori logici]  Le relazioni ad 1 posto su A sono semplicemente i sottoinsiemi di A (la relazione "essere pari" sull'insieme N è l'insieme dei numeri naturali che sono pari).		x   y  output a a V a b V a c V b a F b b V b c V c a F c b F c c V
Nota 2. A volte si trovano anche le scritte  x << y  e  x >> y.  Esse vengono usate per indicare che i numeri x ed y sono tali che x è molto minore o è molto maggiore di y.  Sono notazioni usate spesso nelle applicazioni, ma non sono rigorosamente delle relazioni d'ordine: il loro significato non è definito precisamente, ma dipende dal contesto in cui esse vengono usate. Ad esempio in un contesto economico, pensando a dei valori in euro, in qualche caso posso dire che 20 << 1000 in altri no: avere 1020 € invece di 1000 € a volte è rilevante, a volte no.

  Sia ◊ una generica operazione binaria (a due argomenti) in un insieme A. Si chiamano:

associativa la proprietà:	per ogni x, y e z in A	x◊(y◊z) = (x◊y)◊z
commutativa la proprietà:	per ogni x e y in A	x◊y = y◊x
elemento neutro (o elemento identità) un elemento @ di A tale che:	per ogni x in A	x◊@ = @◊x = x
elemento inverso di un elemento x di A un altro elemento x di A tale che:		x◊x = x◊x = @
È intutivo, ma non è semplice dimostrare, che dall'associatività e dalla commutatività segue la possibilità di riordinare un termine costruito con "◊"

    Ad esempio la struttura dei numeri reali dotata di addizione e moltiplicazione, così come tutte le sue sottostrutture (quella degli interi, dei razionali, dei decimali limitati, …), gode rispetto a tali operazioni della proprietà associativa e commutativa. Ha "0" e "1" come elementi neutri rispetto a tali operazioni. E ogni numero reale x ha il suo inverso rispetto alla addizione (–x, l'opposto di x) e, se è diverso da 0, rispetto alla moltiplicazione (1/x, ovvero x^–1, il reciproco di x).  Mediante l'addizione dell'opposto [ trasformare differenza somma] possiamo definire la sottrazione e mediante la moltiplicazione per il reciproco [ trasformare rapporto prodotto] possiamo definire la divisione.
    Ciò è possibile anche per la sottostruttura dei numeri razionali.  Non tutti i numeri interi e i numeri decimali limitati diversi da 0 hanno invece il reciproco limitato; queste sottostrutture non sono chiuse rispetto alla divisione.  I numeri naturali hanno (tranne lo 0) opposto non naturale; costituiscono una sottostruttura che non è chiusa neanche rispetto alla sottrazione.  Sia nell'insieme dei numeri naturali che in quelli dei numeri interi, dei razionali e dei reali vale, invece, la proprietà distributiva della moltiplicazione rispetto alla addizione.
    Alla voce "strutture numeriche" abbiamo considerato anche altre strutture dotate di addizione per cui valgono associatività, commutatività, esistenza dell'elemento neutro e degli elementi inversi.
    Possiamo differenziare i diversi insiemi numerici anche rispetto a "≤", ossia rispetto all'ordinamento. Ad es. i numeri naturali hanno un primo elemento, cioè un elemento x tale che se y è un qualunque altro elemento si ha x≤y, mentre i numeri interi (e i razionali e i reali) non lo hanno. Per fare un altro esempio tra due numeri decimali limitati x e y vi è sempre un terzo numero decimale limitato, cioè se x<y esiste z tale che x<z<y (basta, ad esempio, prendere la media aritmetica di essi: tra 2.16 e 2.17 cade 2.165); la stessa cosa vale per i razionali e i reali; invece non vale per i numeri interi: tra 7 e 8 non cadono altri numeri interi; questa proprietà è nota come "densità" (parola che rende bene l'idea).

    Vediamo altri esempi di strutture numeriche e non numeriche:

  le stringhe rispetto all'operazione di concatenazione, che è associativa
(in QBasic x$ = "ma"+"ti": y$ = x$+"ta" equivale a x$ = "ti"+"ta": y$ = "ma"+x$),
non è commutativa     ("ca"+"sa" è diversa da "sa"+"ca"),
è dotata di elemento neutro     (la stringa vuota: "ca"+"" è uguale a "ca");
    le stringhe hanno come "≤" l'ordinamento alfabetico, hanno la stringa vuota come primo elemento e godono della proprietà di densità (tra "kis" e "kit" c'è ad es. "kiss").

  le condizioni rispetto agli operatori logici: se conveniamo di considerare "uguali" due condizioni equivalenti abbiamo che:
OR (o | o …) e AND (o & o …) sono entrambe associative e commutative; ogni condizione vera è un elemento neutro per AND ("0=0 AND x<1" = " x<1"); ogni condizione falsa è un elemento neutro per OR ("0=1 OR x<1" = " x<1").

  gli insiemi rispetto a unione (A∪B = {x: x∈A OR x∈B}) e intersezione (A∩B = {x: x∈A AND x∈B}) che:
come OR a AND, sono entrambe associative e commutative; l'universo (vedi la nota seguente) è l'elemento neutro per ∩ (in R, R∩[0,1) = [0,1)); l'insieme vuoto è l'elemento neutro per ∪ ([1,5)∪Ø = [1,5)).
    Valgono, inoltre, la proprietà distributiva di ∪ rispetto a ∩ − (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C) − e quella di ∩ rispetto a ∪ − (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C).
    I sottoinsiemi di un dato universo hanno come "≤" la relazione di inclusione "⊂": A⊂B ("A è contenuto in B") se ogni elemento di A è anche elemento di B; "⊂" ha la proprietà principale che caraterizza le relazioni di ordinamento: "se A⊂B e B⊂C allora A⊂C" (analoga a "se x≤y e y≤z allora x≤z"), ma dati due insiemi A e B non è che si possa sempre stabilire se A⊂B o se B⊂A (ad esempio, all'interno dell'insieme dei poligoni, l'insieme dei triangoli non contiene né è contenuto nell'insieme dei quadrilateri), mentre tra due numeri si ha sempre che uno dei due è minore dell'altro.
Nota.  Quando in matematica si parla di un insieme ci si riferisce a degli oggetti matematici che hanno certe caratteristiche opportunamente definite (come abbiamo fatto ad esempio per R, di cui abbiamo descritto gli elementi precisando come sono fatti) e rispetto ai quali si è definita una nozione di eguaglianza (ad esempio abbiamo visto che nell'insieme delle stringhe 03 e 3, 1.999… e 2.000… sono oggetti diversi, nell'insieme dei numeri sono invece lo stesso oggetto: 03=3,  1.999…= 2.000…).
   Dato un insieme così caratterizzato, possiamo definire dei suoi sottoinsiemi mediante condizioni; ad esempio, all'interno di R possiamo definire {x : esistono due numeri interi M e N tali che M/N = x}, cioè l'insieme Q dei numeri razionali. L'insieme in cui si opera, in cui si costruiscono sottoinsiemi, … nell'ambito di una certa attività viene a volte chiamato universo (o "universo del discorso").
   Se si sa che l'universo è R per costruire al suo interno nuovi insiemi si usano scritture come la precedente: {x : …}; in caso di ambiguità occorre precisare l'universo da cui si pescano gli elementi. Nel caso precedente si dovrebbe scrivere: {x∈R : esistono due numeri interi M e N tali che M/N = x} ("l'insieme degli x appartenenti a R tali che …").
   Dato un insieme A e una funzione F possiamo costruire anche l'insieme {F(x) : x∈A}, ossia l'insieme immagine di A mediante F. Ad es. l'insieme dei numeri pari è {2n : n∈N}.
   Dato un insieme I e un oggetto k (dell'universo) non è detto che si sappia decidere se k sta in I o no: ad esempio vi può essere un'equazione particolarmente complicata di cui sappiamo che ha una soluzione k della quale siamo in grado di generare le cifre con un procedimento di risoluzione numerica senza che siamo in grado di stabilire se k sta in Q o no.
   Se si definisce un insieme mediante una condizione falsa, si ottiene un insieme che non ha elementi (un insieme vuoto). Ad es. {x∈R : x²+1=0}, cioè l'insieme delle soluzioni dell'equazione x²+1=0, non ha evidentemente elementi. È comodo usare il simbolo Ø per indicare "l'insieme vuoto" e scrivere {x∈R : x²+1=0} = Ø invece di dire che l'insieme {x∈R : x²+1=0} non ha elementi.
   Per indicare che A è contenuto strettamente in B (tutti gli elementi di A sono elementi di B, ma non viceversa) si usa scrivere  A B (che sta per A⊂B AND A≠B). Qualcuno usa ⊂ al posto di ⊂, per una forzata analogia con il simbolo ≤.

La rappresentazione grafica delle condizioni come sottoinsiemi (gli ovali nelle figure a lato) di un insieme dato (il rettangolo "arrotondato") in alcuni casi consente di verificare o trovare una proprietà degli operatori logici in modo più semplice rispetto all'uso di "tabelle di verità".     Ad esempio a lato è illustrata l'equivalenza tra NOT(P OR Q) e (NOT P) AND (NOT Q) ["è falso che: x≤1 o x>2" equivale a "x>1 e x≤2"]     Questo studio delle proprietà degli operatori logici fu iniziato dal matematico e filosofo britannico George Boole, vissuto intorno alla metà del XIX secolo; per questo gli oggetti matematici con proprietà analoghe vengono chiamati algebre di Boole.     Se si dispone di un computer, la verifica (non la scoperta) di queste proprietà mediante le tavole di verità, essendo una cosa "meccanica", è naturalmente più veloce e sicura. Ecco ad esempio la verifica in Qbasic e in R della equivalenza precedente: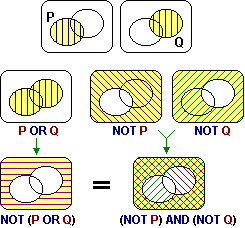
Qbasic: FOR P = -1 TO 0 FOR Q = -1 TO 0 PRINT P; Q, PRINT NOT (P OR Q), PRINT (NOT P) AND (NOT Q) NEXT NEXT	output: -1 -1 0 0 -1 0 0 0 0 -1 0 0 0 0 -1 -1
R: for (p in 0:1) for (q in 0:1) print(c(p,q, !(p|q), (!p)&(!q)))
[comunque si assegnino i valori di verità (V, F) a P e Q le due formule assumono lo stesso valore]

Per una versione in JavaScript clicca qui ed esamina il codice sorgente della pagina  (per altri esempi clicca qui e qui).

[La proprietà precedente, e la analoga - NOT(P AND Q) equivale a (NOT P) OR (NOT Q) - sono note come formule di De Morgan (1806-1871), matematico inglese]

  le funzioni ad input e output in IR
•  rispetto alle "4 operazioni" (il dominio di F+G, F–G e F·G è l'intersezione dei domini di F e di G; nel caso di F/G occorre togliere da tale intersezione gli eventuali x per cui G(x)=0), che godono di proprietà analoghe a quelle dei numeri reali:
gli elementi neutri rispetto a "+" e "·" sono, rispettivamente, le funzioni costanti x 0 e x 1; F ha inverso rispetto alla moltiplicazione solo se non c'è x nel suo dominio per cui F(x)=0.
•  e rispetto alla composizione, che ha la funzione x x (la cosiddetta funzione identica) come elemento neutro e per cui gli elementi inversi sono le funzioni inverse. Si tratta di una operazione che non è commutativa:
se F: x x+1 e G: x 1/x, abbiamo che G(F(x))=1/(x+1) e che F(G(x))=(1/x)+1: G(F(.)) e F(G(.)) hanno domini diversi (la prima non è definita in –1, la seconda in 0), e nel dominio comune non hanno in generale gli stessi valori (ad es. G(F(1))=1/2=0.5 e F(G(1))=2).

  le funzioni polinomiali: sono una sottostruttura rispetto ad addizione, moltiplicazione e composizione dell'insieme delle funzioni a input e output in IR; ammettono elementi inversi solo rispetto alla addizione; come si è visto nella specifica voce hanno proprietà simili a quelle dei numeri interi;

  i vettori rispetto alla somma, già studiati in una specifica voce;

  le trasformazioni geometriche del piano rispetto alla composizione:
•  la sottostruttura delle traslazioni ha, ovviamente, le stesse proprietà della struttra dei vettori rispetto all'addizione sopra considerata: la composizione di traslazioni può essere riordinata, c'è la traslazione opposta, …; analogamente le trasformazioni di scala possono essere riordinate (ci si riconduce a riordinare la moltiplicazione per i fattori di scala) e ammettono l'inverso (basta prendere come fattori di scala i reciproci dei fattori della trasformazione originale);
•  ribaltamenti e rotazioni ammettono l'inverso (un ribaltamento intorno a una retta ha sé stesso come inverso, la rotazione di α attorno a P ha la rotazione di -α attorno a P come inversa), ma non sono commutative, come illustrano le figure sottostanti.

		RA, 90°  poi  RO, 90°	RO, 90°  poi  RA, 90°

  i numeri macchina di una calcolatrice:
•  oltre ad avere il problema che le operazioni non sono definite ovunque (cioè accade nei casi in cui il risultato avrebbe ordine di grandezza troppo grosso o troppo piccolo, eccedendo le capacità di memorizzazione dell'esponente della notazione scientifica: non si può ottenere un numero maggiore di 9.9…9·10⁹⁹ e un numero positivo minore di 1·10^-99), non godono della proprietà del riordino della somma, come si è osservato alla voce  termini equivalenti;
•  essendo in quantità finita hanno un primo elemento (-9.9…9·10⁹⁹) e non godono della proprietà della densità in quanto ogni numero macchina ha il suo successore: se la CT lavora con 8 cifre, a 8.7654321 segue 8.7654322, e non vi sono altri numeri macchina in mezzo (se faccio la media tra i due numeri in questo caso ottengo (8.7654321+8.7654322)/2 = 17.530864/2 = 8.765432, che non è neanche compreso tra i due numeri; non avremmo ottenuto la fuoriuscita dall'intervallo calcolando la media così: 8.7654321+(8.7654322-8.7654321)/2) = 8.7654321 + 5E-8 = 8.7654322).

  La parte della matematica che si occupa delle proprietà delle strutture numeriche e del calcolo simbolico o letterale su espressioni numeriche viene chiamata anche algebra elementare o algebra classica in quanto, ai nostri giorni (a partire dagli inizi del '900), con "algebra" si intende, più in generale, la parte della matematica che si occupa delle proprietà delle strutture sia numeriche che non numeriche, di cui abbiamo visto qualche esempio in questo paragrafo.
    Alcuni chiamano algebra e algebra moderna ciò che qui si è indicato come, rispettivamente, algebra classica e algebra.
    In qualche libro si trova che l'algebra (elementare) sarebbe l'area della matematica che si occupa della risoluzione delle equazioni. Questo non è corretto: come abbiamo visto, per affrontare questo argomento (e inquadrarlo teoricamente) entrano in gioco in modo decisivo anche i concetti di funzione e di continuità, che, volendo fare classificazioni, rientrano nella parte della matematica nota come analisi matematica, di cui si parla in una voce successiva.  L'algebra coincideva con l'area che si occupa della risoluzione delle equazioni qualche secolo fa (vedi), quando esse non intervenivano per lo studio di problemi geometrici e per la modellizzazione di problemi relativi alle pił disparate aree, matematiche e non, quando non venivano rappresentate graficamente, …

Esercizi:

 altri collegamenti     [nuova pagina]