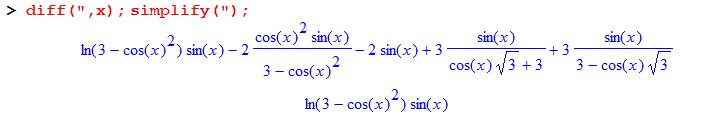| > | Int(sin(3*x),x); |
![]()
t = 3x dt/dx = 3 dx=dt/3 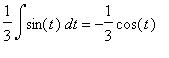
| > | subs(t=3*x,-1/3*cos(t)); |
![]()
Controllo con Maple:
| > | Int(sin(3*x),x) = int(sin(3*x),x); |
![]()
Per calcolare 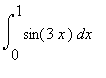 posso fare -cos(3*1)/2 - (-cos(3*0)/2) oppure:
posso fare -cos(3*1)/2 - (-cos(3*0)/2) oppure:
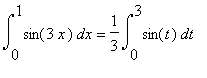 ho applicato t = 3x agli estremi di integrazione
ho applicato t = 3x agli estremi di integrazione
| > | print (Int(sin(3*x),x=0..1), Int(sin(t),t=0..3)/3, int(sin(3*x),x=0..1)); |
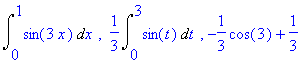
---- (2) -----------------------------------------------------------------
| > | Int(sin(3*log(x))/x,x=1..2); |
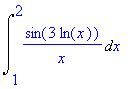
In [1,2] l'integranda è definita e continua. t=3 log(x) dt=3dx/x dx = dt/3*x
| > | diff(3*log(x),x); |
![]()
| > | Int(sin(t),t) = int(sin(t),t); Int(sin(t),t=0..3*log(2))/3 = subs(t=3*log(2),int(sin(t),t)/3)-subs(t=0,int(sin(t),t)/3); simplify(%); simplify("); |
![]()
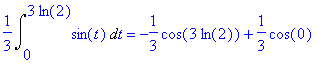
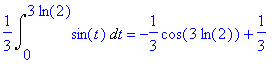
Controllo con Poligon (copia la parte rossa e aziona CLP):
F(x)=SIN(3*LOG(x))/x
[1,2] F INT = 0.4956648059
-4/3*COS(LN(2))^3+COS(LN(2))+1/3 = 0.4956648059885939
OK
Verifica dell'integrale indefinito:
| > | Int(sin(3*log(x))/x,x) = int(sin(3*log(x))/x,x); |
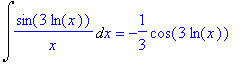
ATTENZIONE: il calcolo diretto dell'integrale definito con Maple in questo caso non avrebbe dato un "bel risultato":
| > | Int(sin(3*log(x))/x,x=1..2) = int(sin(3*log(x))/x,x=1..2); |
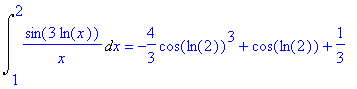
Numericamente invece OK:
| > | Int(sin(3*log(x))/x,x=1..2) = evalf(int(sin(3*log(x))/x,x=1..2),12); |
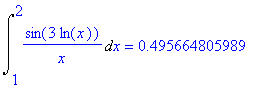
---- (3) ----------------------------------------------------
| > | Int(1/(x^2+4*x+5),x); |
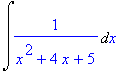
Cerco di usare:
| > | Int(1/(1+x^2),x)=int(1/(1+x^2),x); |
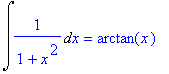
(x+2)^2 = x^2+4x+4 (x+2)^2+1 x+2=t dt=dx
| > | Int(1/((x+2)^2+1),x) = Int(1/(t^2+1),t); |
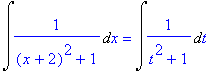
| > | int(1/(t^2+1),t); subs(t=x+2,%); subs(t=x+2,"); |
![]()
![]()
Verifica:
| > | diff(arctan(x+2),x); expand(%); |
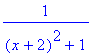
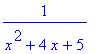
---- (4) ----------------------------------
| > | Int(sin(x)^2*cos(x)^3,x); |
![]()
sin(x)=t dt/dx = cos(x) dx = dt/cos(x) cos(x)^3 dx = cos(x)^2*cos(x) dx cos(x)dx = dt
| > | Int(t^2*(1-t^2),t) = expand(Int(t^2*(1-t^2),t)); int(t^2*(1-t^2),t);subs(t=sin(x),%); |
![]()
![]()
![]()
Verifica (ottengo espressioni diverse; per vedere se sono equivalenti ne faccio la differenza e semplifico):
| > | diff(-1/5*sin(x)^5+1/3*sin(x)^3,x); % - (sin(x)^2*cos(x)^3); simplify(%); |
![]()
![]()
![]()
---- (5) --------------------------------------
| > | Int(cos(3*x)^5,x); |
![]()
t = sin(3x) dt/dx = cos(3x)*3 cos(3x)^4 = (cos(3x)^2)^2 = (1-sin(3x)^2)^2
| > | Int((1-t^2)^2,t)/3; |
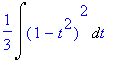
| > | expand((t^2-1)^2); |
![]()
| > | Int(t^4-2*t^2+1,t)/3= subs(t=sin(3*x),int(t^4-2*t^2+1,t)/3); |
![]()
![]()
![]()
![]()
Calcolo diretto e verifica:
| > | int(cos(3*x)^5,x); subs(t=sin(3*x),int(t^4-2*t^2+1,t)/3)-int(cos(3*x)^5,x); simplify(%); |
![]()
![]()
![]()
---- (6) -------------------------------
Come fare a mano:
| > | Int(1/sqrt(a^2-x^2),x) = int(1/sqrt(a^2-x^2),x); |
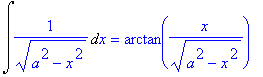
Ci si puo' arrivare pensando a 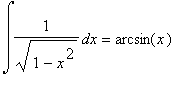 direttamente o usando la sostituzione:
direttamente o usando la sostituzione:
t= x/a dt/dx = 1/a dx = a dt
| > | Int(1/sqrt(a^2-x^2),x) = Int(1/sqrt(1-t^2)*a,t)/a; Int(1/sqrt(1-t^2),t) = subs(t=x/a,int(1/sqrt(1-t^2),t)); |
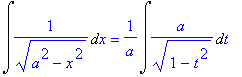
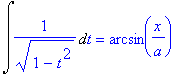
Come mai ho un risultato diverso?
Le due espressioni sono equivalenti? Nel portare fuori a abbiamo supposto che fosse positivo.
Proviamo a mettere l'assunzione a positivo:
| > | assume(a>0); Int(1/sqrt(a^2-x^2),x) = int(1/sqrt(a^2-x^2),x); |
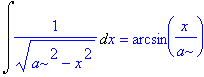
| > | about(a); |
Originally a, renamed a~:
is assumed to be: RealRange(Open(0),infinity)
OK
Togliamo l'assunzione con a := 'a'
| > | a := 'a': about(a); |
a:
nothing known about this object
Vediamo che cosa sarebbe accaduto per a negativo:
| > | assume(a<0); Int(1/sqrt(a^2-x^2),x) = int(1/sqrt(a^2-x^2),x); |
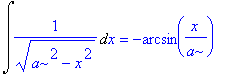
Nel cacolo a mano avremmo dovuto distinguere i due casi.
Togliamo l'assunzione.
| > | a := 'a': |
---- (7) ------------------------------------------------------------
A volte Maple esprime i risultati usando particolari simboli di funzione (i comportamenti possono essere diversi a seconda della versione di Maple). Ecco un esempio:
| > | Int(sqrt(1+4^x)*2^x,x) = int(sqrt(1+4^x)*2^x,x); |
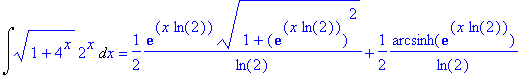
Qui usa le funzioni "iperboliche" (vedi). Si possono operare delle sostituzioni manuali o usare un apposito comando di conversione, per esprimere le funzioni iperboliche mediante il logaritmo e l'esponenziale:
| > | convert(%,ln); |
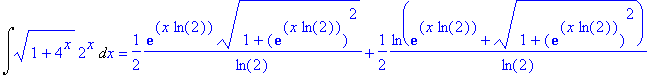
Altro esempio di conversione:
| > | x*tanh(x); convert(%,exp); |
![]()
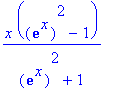
A volte l'uso di simplify o expand e opportune "conversioni" consentono di rendere più leggibili
(e manipolabili) certe espressioni (usa % invece di " in versioni più recenti di Maple):
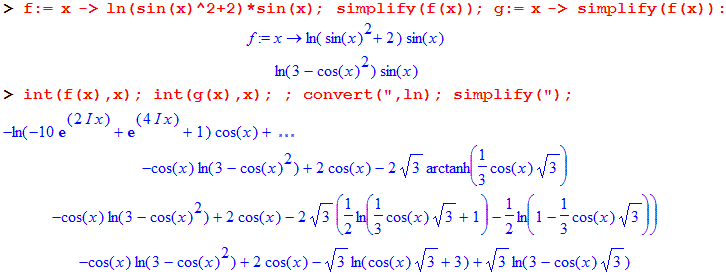
La nuova formulazione della funzione consente (assieme al comando "convert") di manipolarla meglio; in questo
caso di trovarne un integrale in cui non compaiono numeri complessi.
Verifica: