
Convegno Arte e Matematica. Celle Ligure. 27-29 ottobre 2023
Arti figurative e matematica:
collegamenti esplorabili e sviluppabili a scuola
http://macosa.dima.unige.it/alima/celle.htm
Carlo Dapueto (dapueto@dima.unige.it)
|01| La matematica e le lingue storico-naturali hanno molti aspetti in comune: consentono di esprimere idee e descrivere fenomeni, hanno una incessante evoluzione storica,
vivono della loro capacità di comunicare in modo efficace e comprensibile, non hanno un contesto particolare di riferimento, ...
Le altre discipline scientifiche (a parte l'informatica e altri settori di ricerca "figli" della matematica) hanno invece
dei particolari ambiti di applicazione, e tutte si servono della matematica per costruire i loro modelli e, a volte, sollecitano la costruzione o l'invenzione di nuovi concetti e nuovi strumenti matematici.
Questo (l'avvalersi della matematica) vale non solo per le discipline scientifiche ma anche per molte altre discipline (e tecniche), e in particolare per l'arte.
|02| Per i greci, fino all'epoca di Platone, l'arte (tékne) era sia l'artigianato sia tutte le attività fondate su tecnica, abilità e pratica esecutiva. Per i romani il termine ars ha il significato di "attività con fini pratici".
Nel medioevo, grammatica, retorica e dialettica rientravano nelle arti del trivio; aritmetica, geometria, musica e astronomia nelle arti del quadrivio; tutte insieme queste arti venivano indicate come liberali, non servili, contrapposte alle arti meccaniche, servili, dal carattere più tecnico che intellettuale, e fra queste erano comprese le arti figurative.
Progressivamente si arrivò, tra il 1200 e il 1500 (col Rinascimento), al concetto moderno di arte come attività umana volta a
creare un'opera di bellezza, distinta dalla tecnica.
Si è venuta così formando la concezione moderna di arte, che non è più praticata solo a servizio della Chiesa o della nobiltà, ma è da apprezzare in quanto tale, e che comprende, oltre alle
arti figurative (pittura, scultura, architettura), le arti minori (ceramica, vetraria, oreficeria, ...), l'arte musicale, l'arte fotografica, l'arte cinematografica, ...
Qui parleremo delle arti figurative.

|03| Al di là dell'etichettatura come "arte", le prime manifestazioni artistiche (etichettate comunque come tali ad esempio da Picasso), legate alla caccia, risalgono alla fine del paleolitico, decine di millenni avanti Cristo. Nel neolitico (~ 10000-3000 a.C.), con la nascita della pastorizia e della coltivazione, le immagini si fanno più statiche, compaiono i primi segni geometrici:
i bisonti vengono disegnati tutti "eguali", sui vasi di terracotta vengono tracciati segni colorati come ornamenti, si sviluppa il culto dei
morti e sulle costruzioni votate ad esso vengono collocate suppellettili che non hanno funzioni d'uso, vengono realizzate le prime costruzioni "stabili", come i nuraghi. Poi si formano i grandi stati monarchici, la cui cultura artistica avrà una forte influenza sul formarsi della civiltà artistica mediterranea. Si arriva al periodo classico dell'arte greca (IV sec. a.C.), in cui (sia nell'architettura che nella scultura e nella pittura) l'armonia, il rapporto tra le parti e il tutto è collegato ad un interesse teorico e si esprime attraverso leggi
formali che non ingabbiano l'artista ma riflettono una concezione dell'esistenza come relazione dell'uomo con la natura, la società,
il divino. Il divino non è inteso (come avverrà con gli Ebrei) come qualcosa di miracoloso, ma come una umanità
"perfetta", e l'arte mira a mettere in luce questa perfezione. Siamo, ovviamente, lontani anni luce dal classicismo, in cui l'arte
classica viene assunta come modello da imitare.
La matematica interviene, naturalmente, nella realizzazione delle diverse opere ma, anche, nella definizione
di alcuni rapporti tra le dimensioni delle varie parti del corpo umano o, per esempio, tra i diametri di una colonna alle varie altezze di essa.
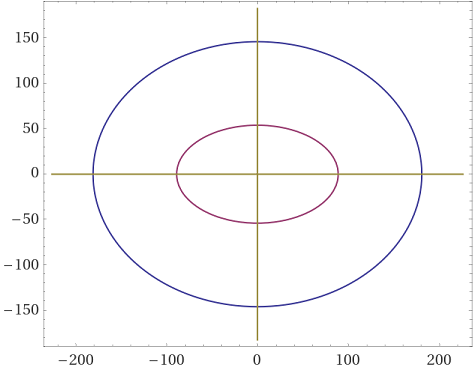
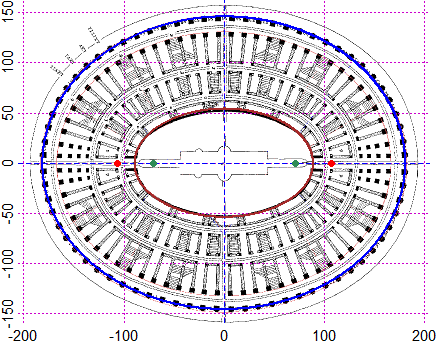
Interviene, ovviamente, anche nella costruzione degli edifici (sotto la forma ellittica del Colosseo).

|04| Dopo questi cenni volti a dare un'idea di come la matematica abbia assunto via via un ruolo sempre più importante nell'ambito delle arti figurative, veniamo al periodo in cui la parola arte assume il suo significato attuale. Come abbiamo già detto, fino al XIV secolo gli artisti non avevano un'arte propria, ma erano aggregati ad attività "simili" (medici, speziali, ...), incluse nelle attività "meccaniche", dette anche "servili", ossia quelle in cui si usavano strumenti, meccanismi, attività fisica. Possiamo far risalire al XV secolo i primi tentativi espliciti di includere l'arte tra le arti "liberali". Un ruolo decisivo lo assunse lo sviluppo delle rappresentazioni prospettiche e il conseguente passaggio degli artisti da "maestri" a "professori". E, invero, anche a "professori di matematica", come vedremo.
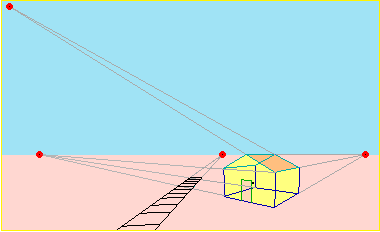
Alcuni punti di fuga (pianura, orizzonte, cielo, binario, casa)
|05| Il taglio storico e interdisciplinare che abbiamo dato a questo intervento non è solo un fatto di forma di comunicazione, ma vuole anche sottolineare l'importanza che le varie discipline trovino nell'insegnamento delle forme di intreccio che facciano percepire agli alunni gli aspetti culturali di esse, spesso oscurati da aspetti nozionistici senza respiro.
|06| Prime avvisaglie della prospettiva

L'ultima cena (Duccio di Boninsegna, 1310 circa)
Gli elementi del cassettone al centro del soffitto hanno un unico punto di fuga. Gli elementi degli altri cassettoni convergono sull'asse di simmetria. Altri elementi del dipinto (come le strisce sulla tovaglia, che sono perpendicolari al quadro come gli elementi del cassettone) non convergono.
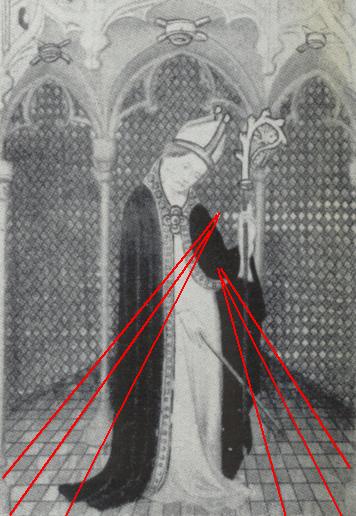
Dipinto della fine del XIV secolo
Le difficoltà a volte vengono superate ricorrendo a "trucchi" quali coprire con personaggi, vesti o festoni le parti del dipinto in cui la prospettiva risulta più difficile, come nel caso di questo dipinto, in cui il personaggio copre la parte in cui vanno a confluire le rappresentazioni delle file di piastrelle.
|07| Padronanza della prospettiva ormai raggiunta
 | Un dipinto facile da interpretare: |
Il punto di vista viene scelto drammaticamente basso. |
 |
|08| Come faccio a raggiungere queste conclusioni? Qual è la matematica che sta dietro alle rappresentazioni prospettiche? Consideriamo un caso semplice, affrontabile in tutti i tipi di scuola superiore: la rappresentazione delle piastrelle (o delle rette parallele nel piano orizzontale).
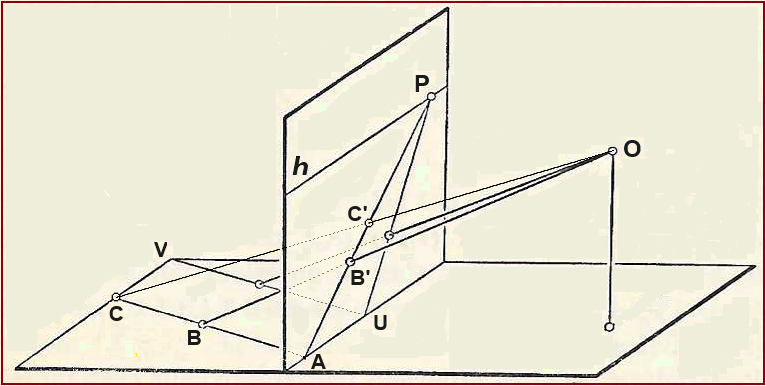
Guardo dal punto di vista O due segmenti uguali e paralleli AC e UV tracciati su un piano orizzontale. Su un vetro verticale passante per AU vedo i segmenti non più paralleli; se prolungassi i segmenti sul vetro li vedrei confluire in un punto P. Se tracciassi altri due segmenti paralleli a partire da A e U li vedrei confluire sul vetro in un altro punto della retta orizzontale h che passa per P. Se prendo B tra A e C sul vetro vedo B' e C' con B'C'/AB' maggiore di BC/AB. La retta h è costituita dai punti "all'infinito" corrispondenti alle varie direzioni (diverse da AU) sul piano orizzontale.
|09| Dopo alcune anticipazioni di Brunelleschi e Leon Battista Alberti, fu Piero della Francesca a fare una trattazione rigorosa della prospettiva, con il De prospectiva pingendi (~1474).
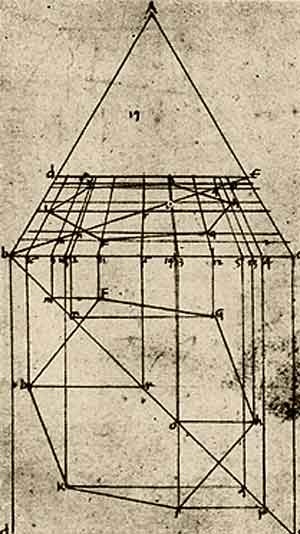 | Le sue spiegazioni non hanno come soggetti esempi pittorici, ma sono argomentazioni e descrizioni di procedimenti di costruzione geometrica generali, che chiama "teoremi". La figura a lato è una delle molte presenti nel suo trattato.
|
|10| Ancora due immagini da manuali di pittura (dei primi anni del '500) del pittore tedesco Albrecht Dürer:
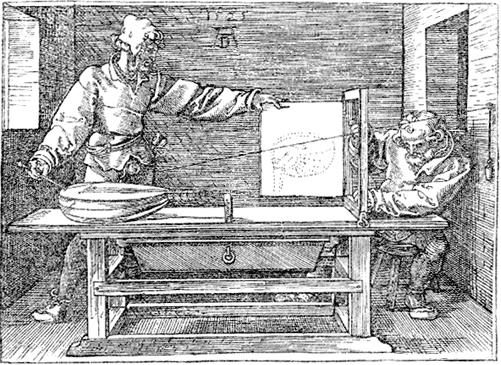

A sinistra la prospettiva come intersezione tra raggi visivi e quadro. A destra come realizzare un disegno in prospettiva utilizzando un reticolo quadrettato collocato verticalmente e un foglio quadrettato (su cui riportare l'immagine vista attraverso il reticolo).
 | Una riflessione organica sulla prospettiva può essere affrontata solo nella scuola secondaria di 2º
grado. Ma un'avvio ad essa deve essere affrontato nei primi anni di scuola, ad esempio
facendo tracciare con un pennarello su un foglio trasparente fissato al vetro dell'aula, tenendo un occhio chiuso, come si vedono una casa, una strada, …,
o facendo realizzare disegni come quelli a lato. |
|11| Nel XVI sec., raggiunta una sicura padronanza della prospettiva, c'è chi la supera, come il Veronese in questo dipinto, in cui sono presenti più punti di fuga (qui ne sono evidenziati alcuni), per mettere in risalto i diversi elementi e dare più respiro alla scena (sono compresenti ben 7 punti di vista).
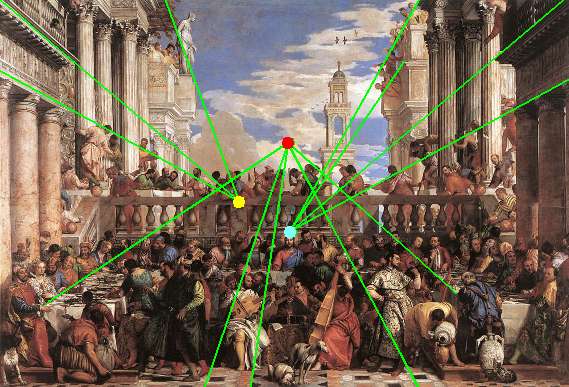
Le nozze di Cana (Il Veronese, 1563)
|12| Con Picasso e il cubismo viene superato l'obiettivo di rappresentare illusionisticamente la profondità:

Les demoiselles d'Avignon (Picasso, 1907)
La superficie del quadro è uno spazio in cui viene organizzata una scomposizione/ricostruzione intellettuale della realtà; entra in gioco anche una quarta dimensione, mentale (e temporale): le figure non sono rappresentate da un unico punto di vista, ma contemporaneamente come le si vedrebbero in diverse posizioni (dell'osservatore e/o dei soggetti), con nasi di profilo su volti frontali, occhi ad altezze diverse, testa e tronco orientati diversamente, …
|13| L'analisi di foto (qui il Loggiato Maggiore del Palazzo Ducale di Genova), offre spunti per significative attività didattiche.
 | Rette parallele tra loro (e non al quadro) vengono viste confluire in uno stesso punto: la balaustra e la sua ombra convergono verso il punto D, le rette che congiungono la base inferiore del blocco su cui poggia una colonna con la base superiore di quello successivo convergono verso il punto E, le ombre di pilastrini e colonne convergono vero il punto A, il lato del porticato perpendicolare a quello visto in primo piano e la linea perpendicolare alla balaustra che separa due tipi di pavimentazione convergono verso B, … Le rette che stanno su piani orizzontali (ombre di colonne, balaustre, profili del tetto, …) convergono tutti sulla stessa retta, AD. Le rette che stanno sul piano delle colonne o su piani ad esso paralleli (come il lato opposto del porticato) convergono sulla stessa retta, DF. | |
Il punto G è quello in cui convergono le rette che congiungono gli elementi reali con le loro ombre: è la posizione del sole. I raggi del sole arrivano sulla terra praticamente paralleli, quindi G è pensabile anche come il punto di fuga di segmenti paralleli diretti come i raggi del sole. | ||
|14| Tocchiamo, rapidamente, altri temi in cui, in qualche modo, si intrecciano matematica ed arte: le tassellazioni, le immagini impossibili, i frattali.
|15| Una tassellazione è la copertura di una superficie (piana o no) utilizzando una o più forme geometriche senza sovrapposizioni e senza spazi vuoti. Due esempi classici:

Un mosaico dell'antica Roma e uno islamico a Marrakech
Non è facile capire come costruire tassellazioni che non siano realizzate con poligoni regolari. Qualche esempio:
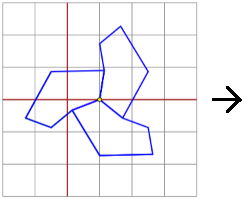 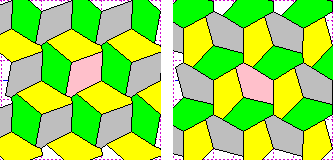 | 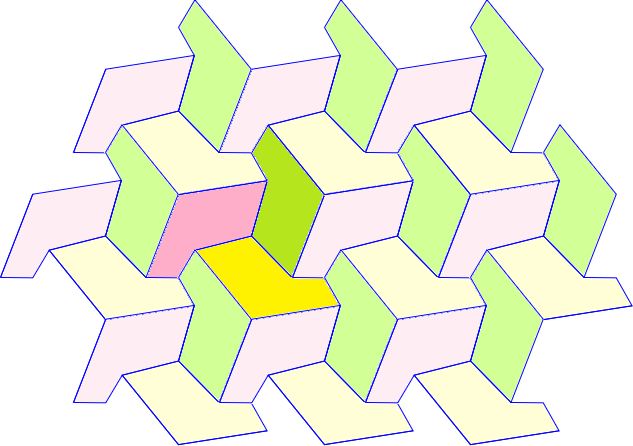 |
Vediamo l'illustrazione della cosa con questa animazione (clicca più volte "riavvia").
Il caso generale è affrontato dal teorema di Escher: vedi
|16| Maurits Cornelis Escher (1898-1972) era un artista olandese (incisore, ma non solo), di cui a fianco riproduciamo la litografia "Cascata" (Waterfall-1961).
 | L'opera rappresenta un moto perpetuo:
l'abilità dell'artista riesce ad ingannare i nostri sensi, facendoci vedere qualcosa che
nella realtà non esiste. |
|17| L'opera precedente richiama un altro aspetto degli intrecci tra matematica ed arte: i paradossi della visione. Alcune immagini e brevi commenti.
 | La presenza di segmentini disposti diversamente su delle rette parallele le fa apparire incidenti. |
La sovrapposizione a dei tratti rettilinei di una sequenza di tratti curvilinei fa apparire incurvati anche i primi. | 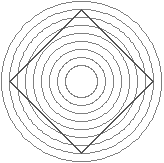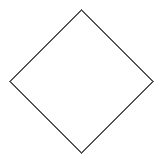 |
 | Anche la presenza di parti colorate diversamente può far apparire linee rette come incurvate. |
Questa figura mette in luce altri limiti della nostra intuizione spaziale: vi sono due segmenti uguali, formati ciascuno da 4 diagonali di quadretto, che a prima vista ci sembrano diversi. | 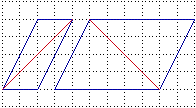 |
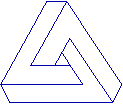 | La figura a sinistra (nota come triangolo impossibile) ci crea un disturbo visivo se la guardiamo globalmente, in tutti i suoi vertici: è l'unione di 3 figure fatte a "7", ma ci richiama l'idea della rappresentazione piana di un solido che non riusciamo a interpretare. |
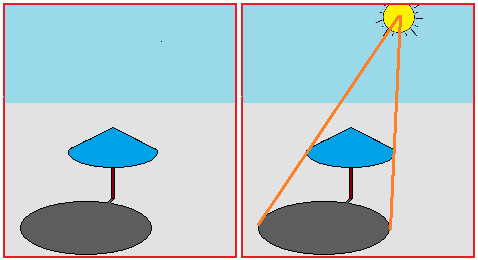
Un "paradosso" apparente, frutto della nostra "ignoranza". Guardo una figura tracciata sul terreno da una distanza di circa 20 m e da un'altezza iniziale di 2 m. Vicino alla figura è collocato un sistema di "assi" di riferimento, con assi finiti (lunghi 10 m ciascuno). La figura sembra un arco di ellisse. Ma man mano che mi alzo (l'altezza passa da 2 m a 60 m) la figura mi appare come una parabola. È possibile che una parabola venga vista come un'ellisse? (pensate al significato di conica! - poi si veda QUI e QUI) |
|
 | Un diversivo (in cui la matematica non c'entra). |
Un altro fenomeno (in cui l'arte non c'entra): l'uomo che appare piccolo in realtà è alto come l'altro uomo, ma è piazzato più lontano. La forma della stanza (chiamata camera di Ames), e la collocazione del punto di vista, danno l'impressione che si tratti di ambiente a forma di parallelepipedo rettangolo. Nel disegno A' rappresenta l'interpretazione della collocazione che dà l'osservazione dell'uomo a sinistra, che in realtà è posto in A. | 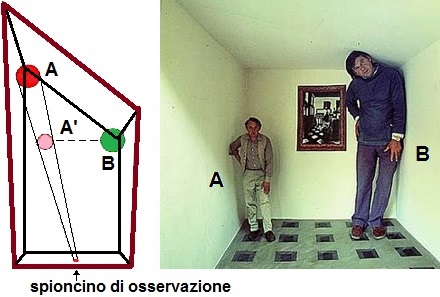 |
|18| Un aspetto importante da considerare a scuola sono anche le semplici trasformazioni geometriche piane che intervengono nell'arte, dalle trasformazioni di scala alle simmetrie. Qualche esempio di figure astratte (con rappresentati gli assi di simmetria) che richiamano, facilmente, opere artistiche che presentano analoghe simmetrie.
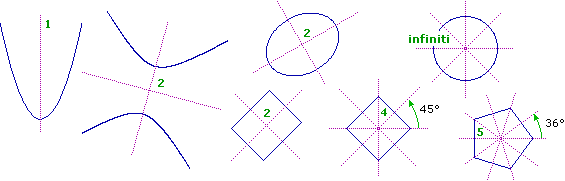
Sotto un mausoleo tipico dell'architettura moghul (Taj Mahal, ~ 1600).

Le simmetrie, nate nell'arte (e nella natura, vegetale e animale), hanno poi assunto un'importanza fondamentale in matematica, anche in statistica. Sotto l'istogramma delle altezze di alcune migliaia di dati relativi alle altezze dei maschi ventenni in Italia nel 1987 (rilevate ad una visita di leva in Italia del 1987), che ha, con buona approssimazione, un andamento gaussiano, quello della "curva a campana" richiamata in una delle opere della galleria "Artisti per la matematica" di Celle.
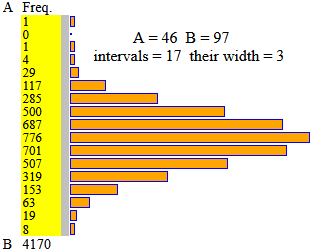
Ma sono pochi i fenomeni con andamento gaussiano. Sotto a sinistra l'istogramma dei pesi delle stesse persone considerate sopra (QUI i dati, QUI uno script per rappresentarli con JavaScript - il software più usato al mondo: quello usato correntemente nella gestione dei servizi su Internet).
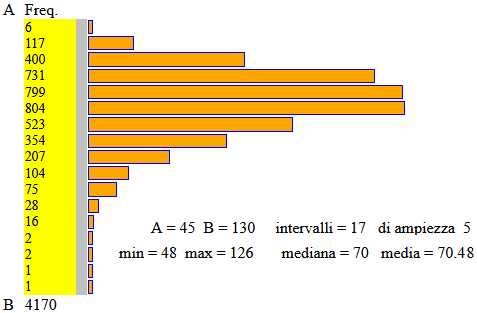
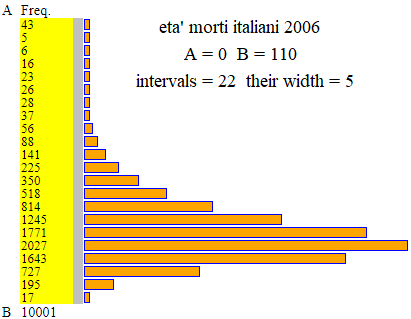
Sopra a destra l'istogramma dell'età dei morti in Italia in un certo anno. Ci sono poi molti fenomeni a cui corrispondono istogrammi approssimati dal grafico di altre funzioni (esponenziali negative, poissoniane, …)
Sotto l'elaborazione statistica di due esempi, ottenuti elevando al cubo dati con andamento gaussiano, entrambi di media 2, con scarti quadratici medi pari, rispettivamente, a 0.2 e 0.6 (potrebbero essere i volumi di cubetti con lati con distribuzione gaussiana; i pesi degli uomini non dipendono cubicamente dalle altezze, ma "quasi", come si intuisce dall'istogramma sopra a sinistra):
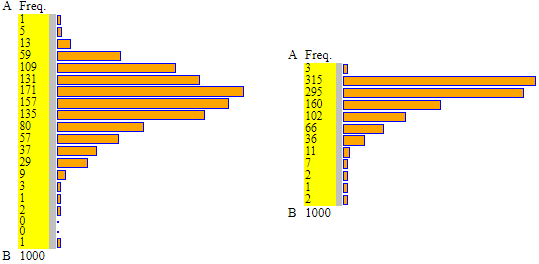
Perché è importante la gaussiana? Perché se Ui sono variabili casuali
con la stessa legge di distribuzione, la media delle Ui
Tornando alle trasformazioni geometriche, nella scuola secondaria di 2º grado si possono matematizzare analiticamente varie trasformazioni geometriche che si trovano in varie opere d'arte e che possiamo riassumere con queste immagini, realizzabili con Paint o altri programmini per disegnare ("qual è la matematica che usa il software per realizzare queste trasformazioni?" è la domanda che si può porre agli alunni).
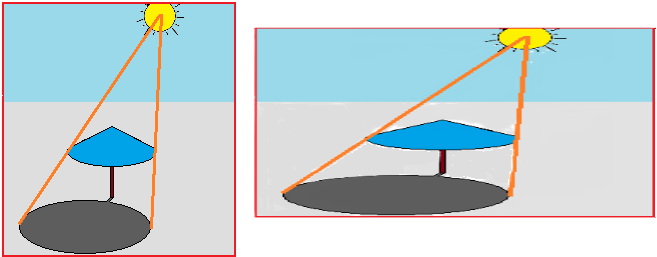
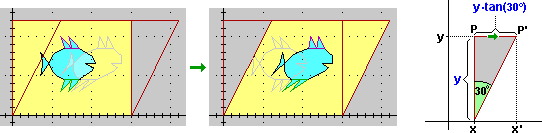
|19| Chiudiamo questa panoramica con qualche cenno all'arte frattale.


Un frattale è la configurazione limite di una successione di figure ottenute una dall'altra mediante una regola assegnata e che ha l'aspetto di una immagine in cui si ripete all'infinito, con grandezza via via più piccola, una stessa forma.
Il nome deriva dal fatto che, data una opportuna definizione di dimensione, a una figura di questo tipo viene assegnata una dimensione frazionaria. La teoria dei frattali è stata elaborata da B. B. Mandelbrot nel 1975.
Vediamo qualche esempio con WalframAlpha (software enciclopedico di matematica, ed altro).
CLICCA e guarda
Koch snowflake (2, 4, 8 iterazioni), Sierpinski gasket (2, 5), Peano curve, Julia set,
Sierpinski tetrahedron, curlicue fractal.
Rivediamo in dettaglio, animato, il frattale Koch snowflake (fiocco di neve)
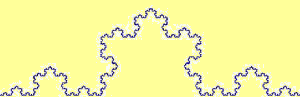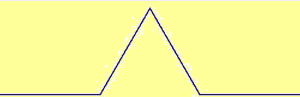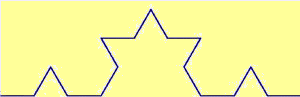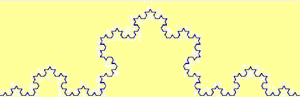
Sul terzo centrale di un segmento lungo 1 viene costruito un triangolo equilatero e viene cancellato il lato che sta sul segmento iniziale. Viene ripetuto il procedimento sui segmenti che formano la nuova figura. E così via. La lunghezza della curva via via costruita quale valore tende ad assumere? (∞)
Un altro esempio animato:

Un semicerchio di diametro 1 viene sostituito da due semicerchi che hanno diametro pari alla metà di esso, hanno un estremo in comune tra loro e l'altro estremo in comune con un estremo del semicerchio di partenza, e stanno da parti opposte rispetto alla retta che passa per gli estremi di esso. Viene ripetuto il procedimento sui semicerchi che formano la nuova figura. E così via. La lunghezza della curva via via costruita quale valore tende ad assumere? (la curva cambia forma ma mantiene sempre la stessa lunghezza, π, mentre la curva limite è un segmento di lunghezza 1!)
Al di là dello studio delle proprietà matematiche dei vari frattali, intorno al 1990 si è sviluppato un vero e proprio movimento artistico denominato arte frattale.

|20| Per indicazioni bibliografiche (in particolare per i riferimenti a Wikipedia - versione inglese!!!) e alcuni approfondimenti
rinvio a questo file online.
Per esempi d'uso di WolframAlpha rinvio a questo.
Per esempi d'uso di JavaScript rinvio a questo.
[ Nella tavola rotonda finale sono stati discussi molti temi. Qualcuno, alla fine del convegno, mi ha chiesto approfondimenti su alcune delle cose che ho detto. Per brevità metto qui dei link ad esercizi in cui tali "cose" sono discusse: chi è interessato apra la sezione di esercizi di "didattica" presente QUI e legga gli esercizi 1.18, 1.27, 1.47, 1.48, 1a.13, 1a.16, 1a.24, 2.2, 2.34, 3.2, 3.11, 3.19, 3.21, 3.25, 3.28, 4.3 e i commenti (cliccando >>>). Se qualcosa non vi convince scrivete (dapueto@dima.unige.it), grazie. ]