modello
e realtà
Su alcuni concetti / temi matematici da affrontare nei primi anni di scuola
("intrecciati" all'interno di unità didattiche)
[scuola primaria - A primaria - B sec. 1º grado sec. 2º grado - A sec. 2º grado - B]
Il concetto di modello
La statistica (e il calcolo delle probabilità)
Il numero e le operazioni aritmetiche
Diagrammi, formule e funzioni
Lo spazio
Rapporti con le altre aree disciplinari
Sono affrontati, con un taglio diverso, più o meno gli stessi contenuti presenti nel documento relativo al livello scolastico successivo.
Le indicazioni sono riferite a quanto mediamente si dovrebbe affrontare nella scuola dell'infanzia e nella prima parte della scuola primaria.
La matematica può essere definita la scienza dei modelli. Il concetto di modello deve dunque avere un ruolo centrale nel suo insegnamento sin dai primi livelli.
Il tema della modellizzazione accomuna tutte le forme di sapere; ciò offre numerose e feconde occasioni di interazioni tra l'insegnamento della matematica e quello delle altre discipline.
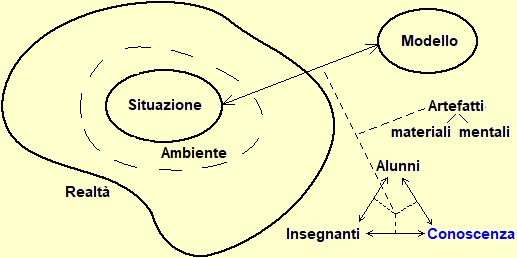
La figura seguente illustra il rapporto tra "modello" e "realtà". Data una situazione reale un modello ne è una rappresentazione semplificata che ne illustra alcuni aspetti, per certe finalità. A seconda delle finalità vi possono essere modelli differenti della stessa situazione (un modello di un aeroplano può avere la stessa forma e colore di un aereo vero ma non volare, o può non assomigliare ad un aereo vero ma volare). La "bontà" di un modello dipende dalla sua adeguatezza agli obiettivi per cui è stato costruito (per evidenziare meglio alcuni aspetti, per generalizzare alcune proprietà, per facilitare il confronto con altre situazioni modellizzate in modo analogo, …). La fase preliminare della modellizzazione circoscrive gli aspetti della realtà coinvolti nel problema che si vuole studiare. Nello schema seguente l'ambiente è la parte di realtà che viene isolata, non dettagliatamente, in questo modo, e la situazione è il complesso degli aspetti del fenomeno da modellizzare (incluse le assunzioni, le intuizioni, le percezioni, le intenzioni, … di chi costruisce il modello) di cui si vorrà tener conto nella rappresentazione:
| modello e realtà |
 |
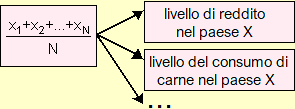
Lo stesso modello può essere impiegato per rappresentare situazioni diverse. Un esempio molto semplice è il concetto di addizione, che può essere usato per indicare il valore complessivo di due quantità di denaro, la temperatura raggiunta dal termometro a partire da un certo valore dopo un certo aumento, il giorno del mese che dalla data odierna verrà raggiunto tra un certo numero di giorni, … Un altro esempio comune è il concetto di media aritmetica, che può essere usato per indicare, in un dato paese, il consumo pro-capite di carne, il reddito medio per famiglia, l'altezza media dei ventenni, …
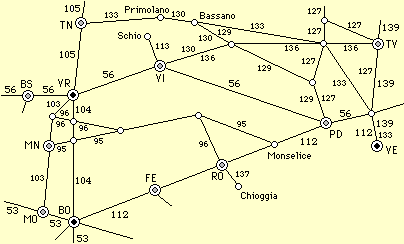
E una stessa situazione, a seconda delle esigenze, può essere rappresentata con modelli diversi. La figura sottostante a destra riproduce parte dell'indice grafico stampato nella prima pagine di un orario ferroviario: è una cartina in cui sono riprodotte le linee ferroviarie e sono indicati i relativi quadri dell'orario; essa è un modello diverso da una usuale cartina geografica in quanto non rappresenta correttamente le distanze e le direzioni.
 |  |
In molti casi occorre reinterpretare il modello verificandone l'adeguatezza a
rappresentare il fenomeno studiato ed eventualmente precisare meglio la situazione da modellizzare.
Nello schema abbiamo messo una doppia freccia
Nella figura sono presi in esame non solo i rapporti modelli-realtà ma anche gli "strumenti" impiegati per costruire i modelli e come la loro messa a punto interagisca col processo educativo, ossia con gli alunni, i docenti e il complesso delle conoscenze (le discipline, le tecniche, …).
I modelli sono rappresentazioni astratte di oggetti o fenomeni "reali" (di tipo materiale: una rappresentazione topografica è il modello di un territorio; di tipo sociale: i concetti di "verbo", "sostantivo", ... sono dei modelli per rappresentare certi elementi della comunicazione verbale; … o di tipo astratto: la "proprietà commutativa" è un modello per descrivere un aspetto di alcune operazioni matematiche).
I modelli sono costruiti utilizzando artefatti cognitivi, ossia "oggetti materiali" (carta, segni, suoni, colori, …) o "costruzioni artificiali" ad hoc (il linguaggio, i concetti, …) che l'uomo usa come protesi della sua mente. Il termine "cognitive artifact" fu introdotto da Donald Norman nel 1993 (Norman D.A., Things that Make us Smart, Wesley Publishing Company, Addison, 1993), mentre quello di "prosthesis tools" fu proposto da Jerome Bruner nel 1986 (Bruner J.S., Actual Minds, Possible Worlds, Cambridge, Mass., Harvard University Press, 1986).
La messa a punto degli artefatti cognitivi per modellizzare le situazioni non avviene episodicamente, ma in un contesto sociale di crescita culturale che viene via via ad organizzarsi in forme strutturate di conoscenza, che vengono trasmesse da una generazione all'altra attraverso processi educativi, in cui gli alunni e i docenti interagiscono tra loro e col sapere, quello in costruzione e quello consolidato. Queste reciproche interazioni sono descritte dal triangolo raffigurato in basso a destra nella figura iniziale.
Quanto osservato sin qui vale per tutte le discipline e le forme organizzate di sapere. Ma la matematica ha la specificità di non essere caratterizzata da una particolare area di problemi o di fenomeni che cerca di modellizzare (come la fisica, la storia, la linguistica, …), bensì dalla tipologia degli artefatti che impiega per la costruzione dei modelli, e che vengono utilizzati in tutte le altre discipline. Quindi lo schema grafico visto sopra (che di per sé è una semplificazione) al fine di rappresentare la situazione dell'insegnamento della matematica deve essere almeno arricchito col tratteggio verticale raffigurato a lato: gli artefatti, per la matematica, presto, da strumenti conoscitivi diventano degli oggetti di conoscenza, da modelli che "astraggono" a partire da situazioni diventano man mano degli strumenti "concreti" per mettere a punto nuove astrazioni, in una spirale senza fine. Il sapere matematico, che nasce dai contesti modellizzati, si organizza internamente non sulla base di questi, ma dei rapporti e delle analogie strutturali tra i suoi artefatti. | 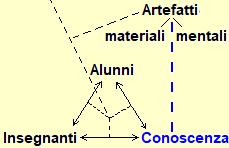 |
La situazione, poi, si fa più complessa in quanto sia il "triangolo", sia la tipologia degli "artefatti", con l'avvento dell'informatica, sono divenute più articolate: il software è diventato un interlocutore "animato" che interagisce tra i diversi soggetti, in modi molto diversi a seconda dell'uso che ne viene fatto e della consapevolezza con cui viene impiegato. Senza complicare ulteriormente la schematizzazione precedente, occorre tener presente che il software ha ora, e avrà sempre più, una incidenza decisiva nel modo in cui i diversi aspetti interagiscono tra di loro.
Riassumendo, possiamo comunque dire che lo studio della matematica si articola nel rapporto (non lineare) tra porsi problemi, modellizzare le situazioni per affrontare la soluzione dei problemi, costruire e ricorrere a teorie che organizzano internamente i rapporti tra gli artefatti impiegati per la costruzione dei modelli e mettono a punto nuovi eventuali artefatti.
Tutto ciò rende cruciale, nell'educazione matematica, il ruolo dell'insegnante. Egli deve:
• progettare e curare percorsi didattici che diano concretezza ad artefatti man mano più lontani da forme elementari di percezione,
• far emergere i conflitti realtà-concetti astratti
(da quelli tra specchi "fisici" e "matematici"
a quelli tra linguaggio "comune" e linguaggio "matematico", ad esempio quando si parla di angoli e lati o
di rettangoli, rombi, …, e ai molti altri presenti sin dalle prime esperienze di insegnamento)
che, se non esplicitati, rischiano di essere fonti di misconcezioni,
mentre, se affrontati, sono un'occasione per trasformare una "opposizione distruttiva" in una "dialettica produttiva", che contribuisca a costruire
un'immagine adeguata della matematica come disciplina,
• educare alla scelta dei modelli (non esiste "il" modello migliore) a seconda delle esigenze e delle "risorse" (artefatti fisici e concettuali) disponibili,
• organizzare l'insegnamento in modo che i riferimenti ad oggetti o situazioni reali non siano solo dei pretesti ma instaurino
dei rapporti virtuosi con le conoscenze (e le motivazioni) extra-scolastiche degli alunni, decentrando, cercando di aver come riferimento
non solo le proprie conoscenze e le proprie motivazioni ma, in un rapporto dialettico, anche quelle degli alunni,
• e dare organicità alle conoscenze da loro man mano acquisite in campo matematico
(anche affiancando allo studio di situazioni problematiche la messa a punto - a partire da esse - di nuovi concetti e
il consolidamento di alcune abilità operative attraverso opportuni esercizi,
che dipendono dal livello delle conoscenze e delle tecnologie storicamente disponibili)
in modo che diventino un solido terreno di partenza per nuove astrazioni,
• tenendo conto che, specie nei primi livelli di istruzione, la costruzione di rapporti virtuosi con l'extra-scuola
dipende anche dal coinvolgimento delle "famiglie": occorre farle partecipare "culturalmente" al progetto educativo che si sta portando avanti
(partecipare "culturalmente" non vuol dire "fare i ripetitori", ma collaborare con i docenti nella costruzione di rapporti tra le attività
scolastiche e la vita extrascolastica); questo è uno dei compiti più difficili; anche questo aspetto andrebbe opportunamente inserito
nel "triangolo didattico" considerato sopra …
QUI trovi qualche esempio che illustra i "i limiti dei modelli".
Questo è un aspetto, accennato anche in precedenza (quando abbiamo osservato che una stessa situazione può essere rappresentata
con modelli diversi) e che viene ripreso anche in punti successivi, a cui è assai importante dare rilievo nell'insegnamento.
La statistica descrittiva (e il calcolo delle probabilità)
| La statistica descrittiva si presta all'introduzione in contesti significativi di molti concetti matematici di base, dai numeri alle approssimazioni, dal concetto di funzione alle rappresentazioni grafiche di relazioni numeriche. Questo, almeno, se la statistica, che più di 20 mila anni fa ha costituito la prima attività di matematizzazione dell'uomo (l'uso delle "tacche" per confrontare quantità di giorni, oggetti, persone, …) e può essere affrontata sin dalla scuola dell'infanzia, non viene ridotta ad essere un tema in più da insegnare separatamente dagli altri temi. Gli strumenti di statistica descrittiva servono poi come punti di riferimento per la successiva introduzione alla probabilità.. QUI sono presenti link a programmi impiegabili per elaborazioni statistiche, che l'insegnante può utilizzare. | 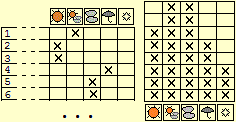 |
La figura precedente si riferiva ad una tipica attività affrontabile nella scuola dell'infanzia (nell'ultimo anno della scuola dell'infanzia si possono registrare su un tabellone le condizioni del tempo e poi si può costruire mese per mese l'istogramma relativo), e che può essere affrontata anche all'inizio della scuola elementare, aggiungendo altre informazioni oltre a quelle meteorologiche (le assenze, annotazioni scritte su fatti significativi, …). Le figure seguenti si riferiscono ad attività analoghe, in cui la rappresentazione grafica si intreccia, operativamente, ai primi usi dei numeri (le colonne degli istogrammi vengono affiancate da numeri che consentono di esprimerne le altezze): a sinistra, i bambini che segnano i luoghi delle loro vacanze (mare, collina, montagna, lago, città) e poi rappresentano queste informazioni su carta quadrettata; a destra segnano analogamente qual è il loro passatempo preferito e poi contano quanti sono quelli che hanno scelto il pallone e la bicicletta.
 |  |
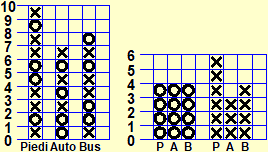
La figura a fianco rappresenta i modi in cui gli alunni di una classe (tutti, e i maschi e le femmine) arrivano a scuola. Gli esempi che stiamo vedendo mettono in luce un altro aspetto: la statistica deve far riferimento inevitabilmente a dei contesti non matematici, e quindi, soprattutto nei primi anni di scuola, offre significative e naturali occasioni di interazioni fra aree disciplinari diverse, e tra aree diverse della stessa matematica, che solo negli anni successivi potranno essere messe a fuoco e divenire oggetto di approfondimento e di consolidamento tecnico. La statistica consente anche di incominciare a mettere bene a fuoco, anche con esempi semplici come questi,
che a seconda di quello che interessa, per lo stesso fenomeno si possono considerare modelli matematici differenti che mettono in luce o trascurano aspetti diversi. |
 |
 |
Nei primi anni di scuola primaria, passando al caso in cui si fanno delle "previsioni", sulla base di considerazioni statistiche, di convinzioni o di informazioni di vario genere, si possono già fare valutazioni probabilistiche.
Non si devono affrontare problemi complessi ma si deve, comunque, mettere a fuoco, facendo riferimento a semplici situazioni, il concetto di "probabile",
che è presente nelle comunicazioni e nei messaggi verbali con cui i bambini hanno a che fare sin dai primi anni di vita. • Con la "ruota della fortuna" riprodotta a fianco, a seconda della parte su cui si ferma la freccia (quella gialla, quella celeste o quella rossa), hai tre premi di valore diverso. Qual è la parte su cui è più probabile che si fermi la freccia? (ovvero, qual è la "fetta" più ampia?) E quella su cui è meno probabile che si fermi? • È più probabile che nevichi a settembre o a gennaio? Perché? • Si sta per disputare la partita Milan-Inter. Per te, chi è più probabile che vinca? |
Sono esempi semplici, ma che sono utili anche come "vaccino" rispetto alle pseudo-definizioni
di probabilità come rapporto casi favorevoli/casi possibili che spesso si trovano nei libri scolastici, ma non solo.
Il numero e le operazioni aritmetiche
Abbiamo già considerato i primi esempi di uso dei numeri nell'ambito statistico. Si tratta situazioni in cui essi sono impiegati per contare. Nelle esperienze del bambino sono comunque presenti molti altri usi dei numeri, richiamati dalle immagini seguenti. Sono numeri usati per individuare delle posizioni (le targhe dei portoni lungo la strada e quelle degli appartamenti all'interno di un caseggiato, i piani raggiungibili con l'ascensore, …, in cui intervengono anche lettere per aggiungere altri "numeri", in cui i numeri possono essere tutti pari o tutti dispari, in cui si usano anche il numero 0 e i numeri negativi, …), numeri che rappresentano degli ordini di arrivo ad uno sportello (e che arrivati a 99 ripartono da 00), numeri di telefono (che i bambini devono imparare a memoria, dicendoli in modo diverso da come si leggono i numeri per contare), i numeri di targa delle auto (in cui non compaiono solo cifre), i numeri degli autobus (numeri per indicare linee, numeri per indicare giorni, numeri per indicare tempi, in ore e minuti), i numeri dei canali televisivi (col telecomando posso fare incrementi e decrementi unitari, e imparo facilmente a scrivere numeri di più cifre), …

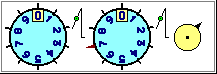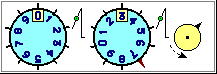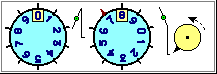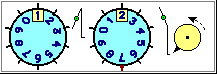
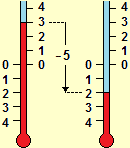
L'uso di 0 come indicatore di una posizione di riferimento (e l'uso dei numeri negativi), oltre che nel caso degli ascensori, è presente in altre situazioni, come nei termometri ambientali (vedi figura sotto a destra) e nei termometri dei frigoriferi. Sotto a sinistra una animazione che può consolidare, operativamente, la comprensione della scrittura posizionale. I numeri per contare, individuare posizioni, misurare temperature, … fanno, inevitabilmente, riferimento anche alle operazioni (incrementi e decrementi) che danno una struttura ai numeri.
|
CLICCA QUI |
 |
 |
Le immagini seguenti illustrano un ulteriore aspetto (concettuale e pratico) della padronanza numerica che deve essere avviato nei primi anni di scuola: l'uso dei numeri per rappresentare e operare con valori monetari, la loro rappresentazione mediante l'abaco, intrecciandosi all'uso degli istogrammi.
| 1 € diviso in 4 parti eguali |
 | 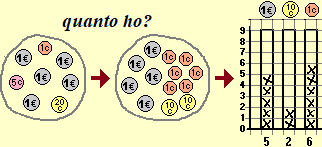 |
Nella vita di tutti, anche delle persone meno scolarizzate, c'è un forte legame tra l'esperienza col denaro e la formazione del concetto "astratto" di numero: per comprendere l'uso funzionale del denaro come strumento per scambiare oggetti tra di loro del tutto differenti occorre astrarre dalla rappresentazione di quantità concrete. Nell'uso del denaro entrano in gioco aspetti cardinali, ordinali, di misura, algoritmici, di scrittura posizionale, … Riflettendo su questo, e sugli altri aspetti messi in luce nei paragrafi precedenti, appare evidente come siano del tutto assurde le proposte didattiche che riducono l'apprendimento numerico allo sviluppo, separato, di abilità ordinali e abilità cardinali.
Negli anni iniziali di scuola occorre consolidare la comprensione dei (e l'interazione tra i) diversi significati dei numeri, in tutti gli alunni, socializzando le loro diverse esperienze, e invitando i genitori, dopo averli coinvolti nel progetto educativo, a far loro sperimentare i diversi contesti d'uso. Alcune immagini che richiamano altre tipiche attività affrontabili (operativamente, senza premature e fuorvianti formalizzazioni, che possono intervenire negativamente sui processi di costruzione del sapere, e del saper fare, che i bambini, individualmente e attraverso interazioni tra pari, stanno attivando):
| le temperature registrate ad un'ora fissata |  |
|
le strisce che riproducono l'altezza delle piantine nel campo di grano (o della piantina di fagiolo o …) o, quando non ci stanno più, in "scala ridotta" (1 quadretto = 2 cm o …) |  |
| quanti minuti sono passati? |
 |


Rinviamo al documento relativo ai successivi anni della scuola primaria per approfondimenti. Ci limitiamo
ad alcune osservazioni.
Non ha alcun senso (né "didattico", né "culturale") affrontare in generale il calcolo in basi di numerazioni generiche.
Altra cosa è avviare (operativamente, con dei "cambi" di unità di misura) all'uso delle notazioni numeriche
impiegate nella misura dei tempi (basi 12, 24, 60), sulle quali gli alunni hanno già competenze operative
acquisite gradualmente nel corso della loro vita.
Abbiamo detto, ed esemplificato, che la formazione della capacità di operare con i numeri va fondata su
modelli concreti e strettamente collegata a situazioni problematiche, per una acquisizione meno superficiale e più duratura. Osserviamo che
con modelli concreti non si intendono affatto i cosiddetti "materiali strutturati" (diffusi da case editrici che hanno come "unico"
obiettivo il profitto), che sono un tipico esempio di modelli astratti. Competenza numerica e padronanza operativa delle proprietà aritmetiche
devono essere consolidate nei "contesti"; grazie alla presenza di questi "prototipi" concettuali,
sarà, poi, possibile trasferirle alle attività con i numeri puri.
Già nei primi anni della scuola primaria gli alunni devono incominciare ad acquisire gradualmente la capacità di passare "in modo spontaneo" da una forma di rappresentazione all'altra dei rapporti d'uso più comune, in particolare facendo riferimento, oltre alla misura del tempo, alle misure dei contenitori di bevande d'uso comune. Questi aspetti saranno occasione, poi, di approfondimento negli anni successivi della scuola primaria.
|
Si può anche, volendo, avviare ad un primo uso delle calcolatrici
tascabili (CT). Ricordiamo che il loro uso è importante nel caso siano presenti alunni con difficoltà di tipo discalculico
(per questo problema rinviamo alle considerazioni svolte QUI nella sezione
dedicata alla scuola secondaria di 1º grado.). Il principale obiettivo dovrebbe essere quello di esplorare (a un primo livello)
alcune conoscenze sui numeri e sulle funzioni (il modo in cui vengono
trasformati i numeri introdotti quando si premono i tasti di funzione
|  |
Può essere utile, specie in queste primi fasce scolastiche, fare ricorso ad immagini animate,
come QUESTE, che sintetizzano i procedimenti eseguiti.
L'uso delle varie rappresentazioni grafiche facilita notevolmente i ragionamenti. È anche il modo attraverso cui le elaborazioni matematiche (relative a indagini sociologiche, situazioni economiche, fenomeni tecnico-scientifici, …) ci vengono in genere comunicate dai mass media. È quindi fondamentale che l'insegnamento educhi sin dai primi anni al loro uso. Nel paragrafo precedente abbiamo già visto molti esempi al riguardo. Le figure seguenti danno un'idea di altre attività a cui, nei primi anni di scuola primaria, si può intrecciare l'uso delle rappresentazioni grafiche: la prima immagine è la riproduzione di un diagramma realizzato dagli alunni di una classe per registrare e rappresentare (settimanalmente) la durata del dì, la seconda contiene i grafici della crescita di diverse piantine in differenti condizioni ambientali, la terza è il grafico della temperatura corporea di una persona ammalata.
| |
| ore di luce e di buio registrate settimanalmente da dicembre a luglio |
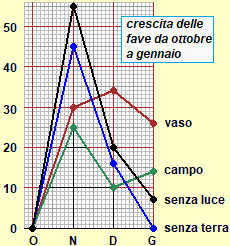 | 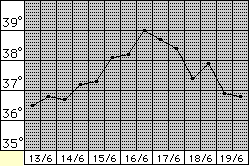 |
Le ultime due figure rappresentano grandezze che variano in funzione del tempo: questi tipi di funzione ad 1 input e 1 output, in cui la variabile indipendente (l'input) è il tempo, sono i più facili da introdurre e quelli che danno più chiaramente l'idea del significato dei grafici. Sotto un esempio più semplice, che nella classe prima dovrebbe precedere il grafico della temperatura corporea.

Il concetto di funzione si intreccia con tutte le aree della matematica. Oltre a queste funzioni, in cui l'output non è generato da un procedimento di calcolo, sono funzioni anche tutte le operazioni su cui ci siamo soffermati nel paragrafo precedente. Sono funzioni anche gli istogrammi a crocette, di cui abbiamo discusso nel paragrafo sulla statistica: ad ogni tipo di località delle vacanze viene associato il numero degli alunni (rappresentato da una colonna di crocette) che le ha passate in quel modo, ad ogni modo di giungere a scuola viene associato il numero di quelli che vi arrivano in quel modo, …
I grafi sono un altro strumento potente, sia dal punto di vista linguistico che da quello matematico, di cui gli alunni capiscono facilmente uso e ruolo: dai primi esempi per descrivere il "cammino" e le "trasformazioni" di alcuni beni (sotto un grafo che descrive, in prima approssimazione, da dove viene il gelato prodotto dalla gelateria) o per scomporre un valore monetario, all'analisi delle voci di costo di un bene (la formazione del prezzo di una bottiglia di vino).

 |  |
Un altro esempio. Come, riflettendo sull'origine dei beni acquistati in un negozio di alimentari, si possono schematizzare i diversi percorsi che uno stesso tipo di prodotto può aver fatto:

Poi, nelle classi successive, i grafi diventeranno uno strumento importante per imparare gradualmente il significato delle formule, per mettere a fuoco le prime convenzioni sulla scrittura dei termini, … e per risolvere problemi alla portata degli alunni ma che non sarebbero in grado di descrivere e "manipolare" mediante equazioni.
Una riflessione sull'impostazione dell'insegnamento geometrico nella scuola primaria è bene che sia affrontata a partire da qualche considerazione generale sull'insegnamento geometrico, che possiamo affidare a questa "digressione", fantastica ma molto concreta, sul concetto di angolo. In essa poniamo il problema di come differenziare, per formalizzazione e sviluppo "tecnico", l'insegnamento dei vari temi nei diversi livelli scolastici. Si è preso come riferimento "simbolico" un tema geometrico perché proprio quest'area della matematica è quella che nell'insegnamento viene affrontata in modo più "dissociato" rispetto allo stato attuale della disciplina.
Alla luce di queste considerazioni, vediamo più in dettaglio quali aspetti dell'educazione geometrica dovrebbero essere affrontati nei primi anni di scuola. Per illustrarli concretamente iniziamo facendo quattro esempi di attività svolgibili tra la fine della scuola dell'infanzia e l'inizio della scuola primaria, che descriviamo nella forma di consegne per i bambini.
| (1) Dei bambini di 6 anni, nei primi giorni di scuola, fanno ad occhi bendati il percorso a lato, segnato da una corda fissata con nastro adesivo sul pavimento del corridoio della scuola. Poi lo descrivono sia a parole (con frasi del tipo "la corda faceva zig-zag, zig-zag tutte eguali", "sembrava una montagna, andava su e giù", …) che con disegni. Due bambini lo rappresentano con i disegni sotto riprodotti. Spiega a parole quali aspetti hanno rappresentato bene e quali no i due bambini. |  |
| (A) |  |  |
(B) |
(2) Sotto vedi parti di due disegni dello stesso campo fatto da un bambino di 6 anni dopo due successive uscite fatte con la sua classe e il suo insegnante. Quale dei due disegni è stato fatto dopo la seconda uscita? Perché?
| (A) |  |  |
(B) |
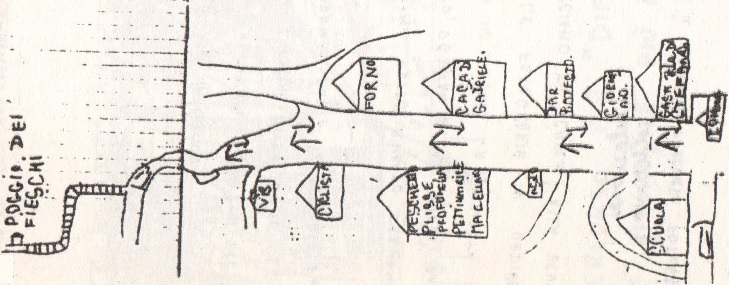
(3) Il disegno di un bambino di 6 anni di un paese della Liguria che rappresenta il percorso fatto per andare con la classe alla chiesa "Poggio dei Fieschi": un pezzo lungo la strada, poi una salita con gradini. L'insegnante dice che nel disegno vi sono cose viste da punti di vista diversi e chiede di spiegare meglio questa osservazione. (Per i docenti: una fase successiva del lavoro in classe può essere quella del confronto con la mappa e/o con la fotografia dall'alto, recuperabile via Internet; occorre stare attenti a non dire "avete sbagliato", ma mettere man mano a fuoco i diversi obiettivi di un disegno con cui non si vuole descrivere solo un percorso ma si vogliono trasmettere anche delle emozioni e delle considerazioni di vario tipo, non comunicabili con una fotografia o una mappa geografica)
(4) Osserva gli oggetti raffigurati e le "orme" sotto ad essi. Le orme sono state ottenute versando della farina sugli oggetti. Nel disegno non sono rispettate le dimensioni né degli oggetti né delle loro impronte. Associa ad ogni oggetto la sua impronta. Spiega a parole perché hai fatto questa scelta. (Per i docenti: L'associazione degli oggetti alle loro impronte è facile, specie se gli alunni hanno fatto delle attività simili "praticamente", versando effettivamente della farina; la cosa più significativa, e utile per le attività che da essa possono originarsi, è la descrizione a parole delle motivazioni, che può essere fatta oralmente o intrecciando considerazioni scritte a discussioni collettive)


Le moltissime immagini presenti nei commenti relative a tutte le altre voci evidenziano come
anche quest'area della matematica sia intrecciata con le rimanenti.
Gli aspetti di questa interconnessione sono essenzialmente due: da una parte per rappresentare e studiare gli oggetti geometrici
entrano in gioco misure di distanze, angoli, estensioni, spostamenti, … e realizzazione o studio di trasformazioni geometriche
che chiamano in causa numeri, operazioni aritmetiche, rapporti e più in generale funzioni,
dall'altra per rappresentare gli altri oggetti matematici (dai numeri alle funzioni, fino alla statistica e alla probabilità)
si utilizzano, sin dalle prime esperienze culturali (non solo didattiche), grandezze e concetti geometrici, come abbiamo già messo in luce con molti esempi.
Facciamo qualche altro esempio per mettere in luce aspetti che occorre incominciare a mettere a fuoco sin dai primi anni.
• Gli alunni devono comprendere che cos'è un angolo (inteso come rotazione con cui passare da un lato all'altro, non come "parte di piano" compresa tra i due lati, modo in cui spesso lo presentano i libri, foriero del misconcetto per cui, nella figura seguente, l'angolo A è maggiore dell'angolo B):

• Devono capire (attraverso discussioni, esplicitando verbalmente il ragionamento seguito) perché misurando la lunghezza della tavoletta di cioccolato raffigurata sotto è errato concludere che la tavoletta è lunga circa 6 cm.
|
• Devono acquisire (attraverso esperienze, osservazioni, disegni, visualizzazione di immagini ottenute con una fotocamera, …) la capacità di associare visioni a punti di vista:
|
• Le attività di disegno a mano libera (e quelle di disegno di case, vie, giardini, … di cui vengono tracciati i contorni su fogli trasparenti appesi alle finestre della classe, quelle di riproduzione fotografica, …) sono occasioni importanti per l'educazione spaziale, intrecciata in modo significativo ad altri aspetti educativi. Un aspetto importante è anche la raffigurazione delle ombre, da affrontare prima liberamente nel contesto di disegni inventati dagli alunni e poi con riflessioni legate ad osservazioni dirette di ombre generate dal sole o da una lampada, a cui far seguire attività di verifica (o di spunto per nuove esperienze) come quella di spiegare a parole quale o quali delle tre figure A, B e C sottostanti sono sbagliate e perché:
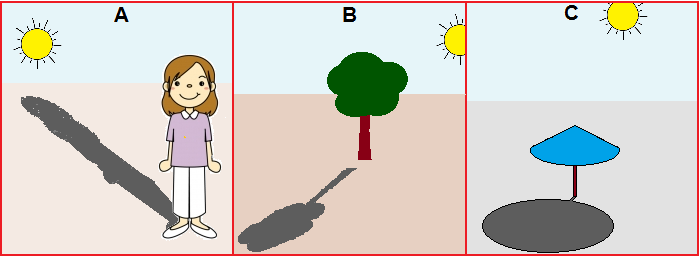
Rinviamo alle considerazioni sul concetto di "spazio" nelle parti dedicate ai successivi livelli scolastici.
Come già detto, i concetti dovranno essere ripresi e approfonditi successivamente, nell'ottica di una ripresa a "spirale" degli argomenti: come sottolineano anche i programmi scolastici da moltissimi anni, non si tratta di fare degli "anticipi", ma di utilizzare, in modi opportuni, terminologie e concetti che trovano naturali intrecci con altri concetti e di porre le basi per la costruzione di successivi livelli di formalizzazione. Ci pare fondamentale questo aspetto, sia per dare una immagine corretta e "viva" della matematica, sia per non favorire irrigidimenti mentali che identificano i concetti con particolari definizioni, particolari procedimenti di calcolo, … e li classificano in aree (la geometria, l'aritmetica, …) non comunicanti tra loro. QUI si possono trovare vari esercizi che esemplificano le considerazioni svolte in questo paragrafo.
Rapporti con le altre aree disciplinari
Nel paragrafo inziale, sul concetto di modello, abbiamo discusso a lungo dei rapporti
tra la realtà e i vari modelli, disciplinari e non, con cui essa, o suoi aspetti particolari, possono essere rappresentati e studiati.
Abbiamo messo in luce anche le differenze tra i modelli matematici e gli altri modelli disciplinari, e le attenzioni didattiche che tutti questi aspetti
devono sollecitare in chi ha il compito di educare le nuove generazioni, soprattutto nelle prime fasce scolastiche.
Mentre le altre discipline si riferiscono a diversi tipi di fenomeni, la matematica è caratterizzata dal tipo di artefatti
che impiega ed è organizzata sulla base della loro proprietà e dei rapporti formali tra essi, anche se alcuni settori di confine (l'informatica, l'econometria,
la fisica matematica, …) sono caratterizzati dalla relazione con certe discipline e aree teconologiche.
Ma, come abbiamo evidenziato sopra, la nascita e lo sviluppo storico dei vari
concetti matematici si è intrecciato agli altri saperi, e la capacità di utilizzare gli artefatti matematici dipende dalle
conoscenze dei contesti in cui essi vengono impiegati. Nel lungo percorso di apprendimenti scolastici ed extrascolatici attraverso il quale si diventa
adulti, cose inizialmente acquisite come astrazioni diventano poi degli "oggetti" concreti per descrivere "realtà" su cui realizzare nuove astrazioni.
Ma, affinché questo processo si sviluppi in modo efficace, occorre che questo passaggio concreto-astratto sia graduale, sia "percepito" dagli alunni,
faccia riferimento ai vari aspetti conoscitivi con cui nella vita di tutti i giorni essi hanno a che fare, per arrivare progressivamente a forme
organizzate disciplinarmente.