mesi n.pezzi costi  gen   5500   5400 feb   6500   5600 mar   4500   4800 apr   3000   4800 mag   3500   4900 giu   3200   4600 set   5000   5300 ott   6000   5400 nov   7500   5800 dic   8500   6000

Una azienda meccanica ha rilevato che in un dato anno, da gennaio a giugno e da settembre a dicembre, un suo reparto ha prodotto le seguenti quantità di pezzi coi costi (in €) indicati a lato. Prova a rappresentare i dati graficamente e vedi se è possibile approssimare la relazione tra numero dei pezzi prodotti e costi con una opportuna funzione.

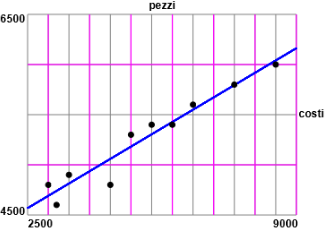
Si vede che i punti si dispongono approssimativamente lungo una retta. Ecco come tracciare una retta che li approssima con R. Più avanti vedrai metodi matematici per trovare una retta di questo tipo "numericamente" (vedi sotto).

source("http://macosa.dima.unige.it/r.R")
pezzi <- c(5500,6500,4500,3000,3500,3200,5000,6000,7500,8500)
costi <- c(5400,5600,4800,4800,4900,4600,5300,5400,5800,6000)
c( min(pezzi),max(pezzi),min(costi),max(costi) )
#     3000    8500            4600    6000
Piano(3000,9000, 4500,6500)
PUNTI(pezzi,costi, "black")
suassex("pezzi"); suassey("costi")
# La pendenza di una retta che passi "vicino" ai punti
frazio((6200-4600)/(9000-3000))
# 4/15
f = function(x) 4600+(x-3000)*4/15
# ovvero, semplificando:    0.2666… * x + 3800
grafi(f,3000,9000, "blue")

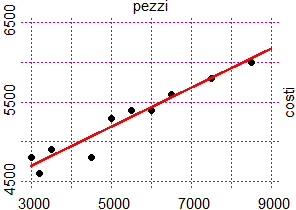
Ecco, per inciso, che cosa si otterrebbe utilizzando la regressione ( l'correlazione), con R:

pezzi <- c(5500,6500,4500,3000,3500,3200,5000,6000,7500,8500)
costi <- c(5400,5600,4800,4800,4900,4600,5300,5400,5800,6000)
c( min(pezzi),max(pezzi),min(costi),max(costi) )
#     3000    8500            4600    6000
Piano(3000,9000, 4500,6500)
PUNTI(pezzi,costi, "black")
suassex("pezzi"); suassey("costi")
regressione1(pezzi,costi)
#  0.2454 * x + 3954 
g = function(x) 0.2454 * x + 3954
grafi(g, 3000,9000, "red")

che posso arrotondare con  y = 0.245*x + 3950

Il grafico realizzato con questo: