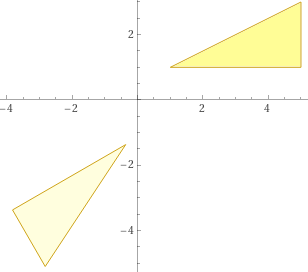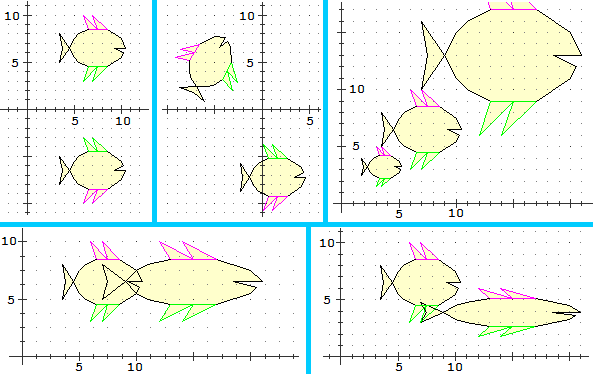
Esprimi, come preferisci, ma in modo comprensibile ed esauriente, come trasformare una figura nell'altra, o nelle altre, nei seguenti 4 casi (i sistemi sono monometrici). Come vengono modificate le aree nei vari casi?

La 1ª illustrazione contiene una figura (una qualunque delle due) trasformata nell'altra
mediante un ribaltamento rispetto all'asse orizzontale. Indicando con x e y ascisse e ordinate, e con
x' e y' quelle della figura trasformata,
possiamo rappresentare la trasformazione con le equazioni y' = −y e x' = x.
Nel caso della 2ª illustrazione è chiaro che siamo di fronte a due figure una
simmetrica dell'altra rispetto a una retta opportunamente inclinata. Cerchiamo di individuare,
approssimativamente, tale retta. Se tracciamo l'asse di simmetria (come asse dei segmenti
che congiungono un punto al suo corrispondente) e sovrapponiamo un goniometro
troviamo che l'asse è, con buona approssimazione, la retta passante per O con inclinazione
di 30° (ossia la retta y =
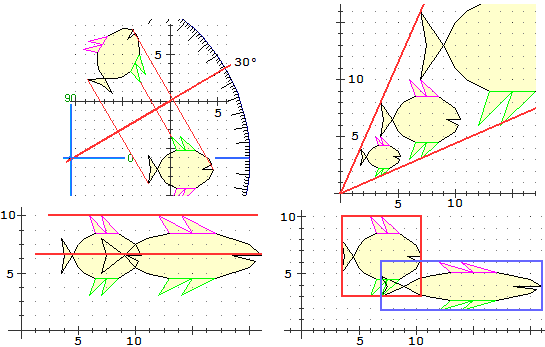
Nella 3ª illustrazione capiamo, e possiamo evidenziare con le semirette
tracciate sopra, che si tratta di ingrandimenti/riduzioni, ovvero di tarsformazioni di scala momometriche.
Fecendo riferimento a come si trasforma un particolare, ad es. la punta delle pinna in basso a sinistra
o quella in alto della coda, possiamo osservare che passando dal pesce più piccolo via via
al più grosso le coordinate vengono man mano raddoppiate. Se indichiamo con x e y le coordinate
di un punto del pesce più piccolo, con x' e y' quelle del corrispondente punto del pesce intermedio,
e con x" e y" quelle del punto corrispondente del pesce grosso, abbiamo x' = 2x, y' = 2y,
y' = y2/2, x' = x"/2, x" = 4x, y" = 4y, y" = 2y', x" = 2x', y = y'/2, x = x'/2,
y = y"/4, x = x"/4.
Nel caso della 4ª illustrazione abbiamo che vengono ingrandite, e più
precisamente moltiplicate per 2, solo le ascisse: la trasfomazione dal pesce piccolo al
pesce grosso è descrivibile come x' = 2x, y'=x. Quella dal grande al piccolo con
x'=x/2, y'=y.
Nel caso della ultima illustrazione abbiamo che vengono ingrandite, e più
precisamente moltiplicate per 2, le ascisse; le ordinate vengono invece moltiplicate per 0.6,
come si capisce dalla posizione più alta del pesce, che passa da 10 a 6, e da quella
più bassa, che passa da 4 a 2: la trasfomazione dal pesce a sinistra a
quello a destra è descrivibile come x' = 2x, y'=y·0.6. Quella opposta
con x' = x/2, y' = y/0.6 = 5y/3.
Le prime due trasformazioni non modificano le aree. La terza le moltiplica per un fattore che è il quadrato della scala lineare. La terza le moltiplica per il fattore per cui vengono moltiplicate le ascisse. La terza, in un verso le moltiplica per 2·0.6 = 1.2, nel verso opposto per 1/2·5/3, ossia per 5/6, che è il reciproco di 1.2 (1/1.2 = 10/12 = 5/6).
Per altri commenti:  Trasformazioni geometriche
neGli Oggetti Matematici
Trasformazioni geometriche
neGli Oggetti Matematici
Nel caso si volessero preparare esercizi analoghi ecco come si possono realizzare figure simili con R (vedi qui):
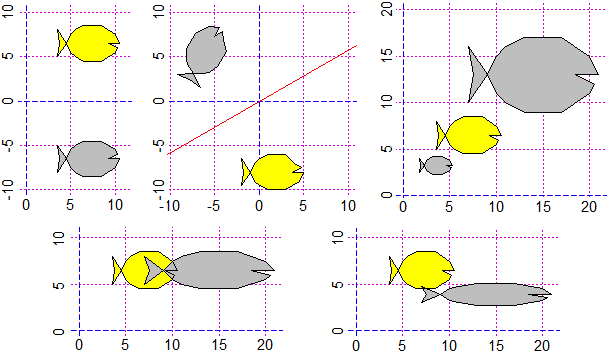
... o con lo script online "disegnare(4)": vedi (leggi l'help per costruire questa figura).
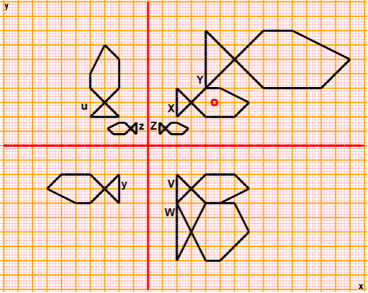
Possiamo realizzare figure analoghe anche con WolframAlpha:
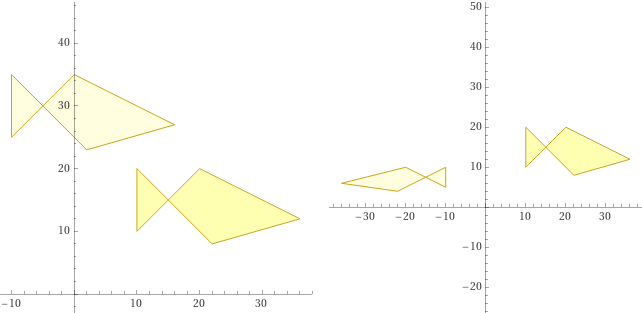
La prima figura (pesce trasformato con x → x-20, y → y+15) è realizzata con questi comandi:
polygon{(10,10),(20,20),(36,12),(22,8),(10,20)}, polygon{(-10,25),(0,35),(16,27),(2,23),(-10,35)}
La seconda (x → -x, y → y/2) con questi:
polygon{(10,10),(20,20),(36,12),(22,8),(10,20)}, polygon{(-10,5),(-20,10),(-36,6),(-22,4),(-10,10)}
Altre figure (x → -x; y → -y; x → x/2-5, y → -y/2) con questi:
polygon{(10,10),(20,20),(36,12),(22,8),(10,20)}, polygon{(-10,10),(-20,20),(-36,12),(-22,8),(-10,20)}
polygon{(10,10),(20,20),(36,12),(22,8),(10,20)}, polygon{(10,-10),(20,-20),(36,-12),(22,-8),(10,-20)}
polygon{(10,10),(20,20),(36,12),(22,8),(10,20)}, polygon{(0,-5),(5,-10),(13,-6),(6,-4),(0,-10)}
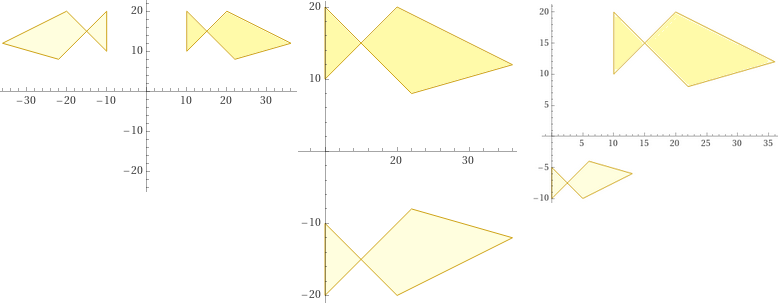
Posso realizzare le immagini in una stessa parte di piano cartesiano aggiungendo, ad esempio, ad ognuno dei precedenti comandi:
, polygon(-40,0),(40,0),(0,0),(0,-40),(0,40),(0,0)
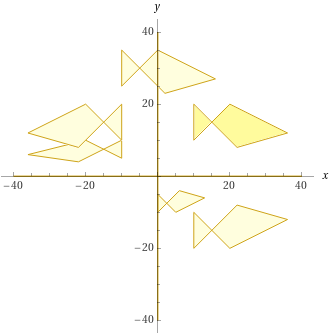
Posso via via incollare le immagini ottenendo:
Per ruotare (x,y) di A attorno a (0,0) occorre applicare (x,y) → (x*cos(A)-y*sin(A), x*sin(A)+y*cos(A)). Un esempio (rotazione di 210°):
polygon(1,1),(5,1),(5,3), polygon(1*cos(210°)-1*sin(210°), 1*sin(210°)+1*cos(210°)),(5*cos(210°)-1*sin(210°), 5*sin(210°)+1*cos(210°)),(5*cos(210°)-3*sin(210°), 5*sin(210°)+3*cos(210°))