Sistemi di variabili casuali

    Approfondiamo lo studio dei rapporti tra variabili casuali, già avviato introducendo i concetti di dipendenza e indipendenza stocastica.

  Esempio 1

Due tipi di cadute a caso di proiettili in un bersaglio.  Vogliamo stimare sperimentalmente la probabilità che, prendendo "a caso" un punto in un bersaglio composto da due cerchi concentrici con raggi uno doppio dell'altro, il punto cada nel cerchio centrale.  Consideriamo due possibili procedimenti, di cui puoi esaminare una versione come "script" (bersaglio) o in R (vedi qui), mediante i quali viene generato un punto che cade nel cerchio di centro O=(0,0) e raggio 1 e verificato se la sua distanza da O è minore di 1/2 (ovvero se il quadrato di essa è minore di 0.25):

x=random()*2-1; y=random()*2-1; if (x*x+y*y<1) {lanci=lanci+1; if (x*x+y*y<0.25) {ok=ok+1} }

r=random(); a=random()*atan(1)*8; x=r*cos(a); y=r*sin(a); lanci=lanci+1; if (x*x+y*y<0.25) {ok=ok+1}

Con il primo procedimento ottengo esiti simili ai seguenti:
n.lanci   % OK 7856   25.58554	Col secondo:	n.lanci   % OK 10000   50.01

Rappresentazione grafica con gli script: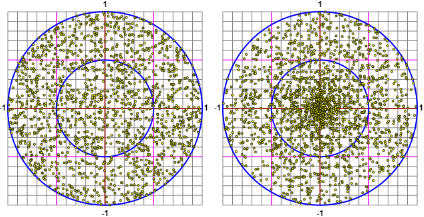

    I due procedimenti generano i punti in modo diverso: mentre il primo usa il generatore di numeri casuali per ottenere un punto nel quadrato [–1,1]×[–1,1] e lo prende in considerazione solo se dista da O meno di 1 (if (x*x+y*y<1) …), il secondo evita di questo controllo generando direttamente un punto (in coordinate polari: a = direzione, r = distanza da O) che cade nel cerchio.

   Mentre col primo i proiettili si distribuiscono in modo uniforme nel cerchio, col secondo si distribuiscono concentrandosi maggiormente intorno a (0,0). Mentre col primo la frequenza tende a stabilizzarsi su 1/4, pari al rapporto tra area del centro e area del bersaglio, col secondo tende a stabilizzarsi su 1/2: il fatto che il punto generati disti meno di metà raggio dal centro dipende solo dal valore di r, che essendo con distribuzione uniforme in [0,1), ha il 50% di probabilità di essere minore di 1/2.

    Si tratta di due cadute casuali con diverse leggi di distribuzione.

    Qui stiamo estendendo il concetto di legge di distribuzione dal caso di una variabile casuale U a valori numerici al caso di U = (X,Y) con X e Y variabili casuali a valori in IR .  Questo viene chiamato anche caso bivariato; si dice anche che U è un sistema di variabili casuali.

  Esempio 2

La tabella a lato rappresenta la distribuzione delle variabili Sesso e Settore di attività (classificato in "agricoltura", "industria", "altre attività") in cui una persona (in Italia nel 1991) era occupata: per ogni possibile coppia (Sesso, Settore) è indicata la corrispondente frequenza assoluta. Una tabella "a doppia entrata" come questa, in cui sono indicate le frequenze o le probabilità di due variabili casuali viene detta tabella di contingenza (se ne è già fatto uso alla voce dipendenza e indipendenza).   settore M F agricoltura 1.17 0.66 industria 5.26 1.66 altre attiv. 7.68 5.18 totale 14.10 7.49 (1991; dati in milioni)     Calcolando le distribuzioni percentuali riga per riga (vedi seconda tabella nella figura sottostante, che, come la seguente, puoi cliccare per ingrandirla) posso valutare meglio le relazioni di dipendenza/indipendenza tra le due variabili. Concludo immediatamente che le variabili "sesso" (a uscite: M, F) e "settore" (a uscite: agr., ind., altro) non sono indipendenti: le righe dei dati non sono più o meno proporzionali (ovvero le righe delle percentuali non sono più o meno uguali). Posso invece ritenere indipendenti "sesso" (degli occupati) e "occupazione in agricoltura" (a uscite: sì, no): 1ª e 4ª riga sono "quasi" proporzionali.   A volte, nella manipolazione delle tabelle di contingenza, si usano alcune terminologie specifiche (distribuzioni marginali, profili riga e colonna), richiamate (riferendosi al nostro esempio) nelle figure sopra e sottostanti, che illustrano anche come un foglio di calcolo elettronico può essere utile per rappresentare (percentualmente e graficamente) ed elaborare tabelle di dati (i dati sono stati scritti nel "rettangolo" B2-C4, le elaborazioni numeriche sono state ottenute con le 4 "formule" riprodotte, che sono state "estese" verticalmente od orizzontalmente alle altre celle, con una modifica automatica dei "riferimenti" ai dati da elaborare; l'istogramma rappresenta sia la distribuzione di Settore che le tre distribuzioni condizionate di Sesso).     Possiamo rappresentarne completamente la distribuzione con un istogramma tridimensionale, come quello sotto a sinistra: le altezze delle colonne rappresentano le frequenze relative; le altre figure rappresentano le distribuzioni percentuali delle due variabili.  Qui trovi come elaborare i dati mediante R. [1°, 2°, 3° stanno per "primario", "secondario", "terziario"]   Rappresentazione grafica delle leggi di distribuzione     Nel caso di una singola variabile a valori in un intervallo di numeri reali realizzavamo un istogramma classificando le uscite in intervallini; analogamente, nel nuovo caso, possiamo rappresentare le distribuzioni classificando le uscite in tanti rettangolini.     Sotto è rappresentata la legge di distribuzione di U=(U1,U2), esito del lancio di due dadi equi; in questo caso le altezze degli istogrammi corrispondono alle probabilità Pr(U=(i, j)) con i e j in {1, 2, …, 6}; questa è una distribuzione uniforme finita: le probabilità Pr(U = (i,j)) sono tutte uguali, a 1/NumeroUscitePossibili = 1 /(6·6) = 1/36.  Il secondo e terzo istogramma rappresentano solo le parti superiori delle colonne, evidenziando meglio che si tratta di una distribuzione uniforme.     Nel caso dell'esempio iniziale, la caduta dei proiettili, siamo di fronte a un sistema (X,Y) di variabili casuali non discrete. Un'idea della distribuzione mi è fornita dal grafico di dispersione (scatter diagram), ossia dalla rappresentazione grafica delle coppie di uscite sperimentali:     Per una rappresentazione tridimensionale osserviamo che, come nel caso di una singola variabile a valori in un intervallo di numeri reali realizzavamo un istogramma classificando le uscite in intervallini, analogamente, ora, possiamo rappresentare le distribuzioni classificando le uscite in tanti rettangolini la cui unione copra il dominio delle uscite. Ecco possibili rappresentazioni per i due tipi di cadute, in cui le colonnine sono state separate per facilitare la "lettura".  [vedi qui se vuoi ottenerle con R]     Nel caso di una variabile continua X all'aumentare delle prove e all'infittirsi della partizione il contorno superiore dell'istogramma sperimentale (normalizzato, in modo che sia di area 1) tende a stabilizzarsi su una curva tale che Pr(h ≤ X ≤ k) corrisponde all'area delimitata da curva, asse orizzontale e rette di ascissa h e k.     Analogamente nel caso di una variabile U = (X,Y), se all'aumentare delle prove e all'infittirsi dei rettangolini il contorno superiore dell'istogramma tridimensionale (in cui ogni colonnina abbia altezza pari alla frequenza relativa divisa per l'area del rettangolino di base, in modo che il volume complessivo sia 1) tende a stabilizzarsi su una superficie che sottende uno spazio di volume 1, il calcolo delle probabilità può essere ricondotto al calcolo di volumi. Sotto sono raffigurate queste "superfici limite", che rappresentano le leggi di distribuzione dei due tipi di cadute. Analogamente al caso univariato, le funzioni di due variabili sul cui grafico tendono a stabilizzarsi gli istogrammi sperimentali si chiamano funzioni di densità.     Sotto sono raffigurate la funzione di densità f corrispondente al secondo caso e alcune relative curve di livello (vedi qui come realizzarle con R). Tenendo conto che, per come sono generati i punti, il grafico deve essere simmetrico rispetto all'asse z e del fatto che la probabilità che un punto cadi a meno della distanza R da (0,0) è R, si può ricavare che si tratta della superficie generata dalla rotazione attorno all'asse z di una curva del piano xz che ha l'asse z come asintoto verticale. La figura non è limitata superiormente, ma ha volume finito (uguale ad 1).     Osserviamo che, come abbiamo già visto che una superficie illimitata può avere area finita ( leggi di distrib. var. discrete), così un solido illimitato può avere volume finito.     Qual è la funzione densità della variabile U = (X,Y) corrispondente al primo tipo di caduta?  È la funzione che a ogni (x,y) del cerchio associa il valore 1/π e agli altri punti associa 0. Il volume del cilindro verticale che essa delimita assieme al piano z = 0 ha volume 1.     A lato è raffigurato il grafico di una funzione densità f. Il cerchio di base ha raggio 1 (per (x,y) esterno al cerchio assumo f(x,y)=0). Come sono fatte le curve di livello di f? Quanto vale f(0,0)?  Le curve di livello sono cerchi concentrici.  Il volume è 1, per cui il cono deve essere alto 3/π: questo è f(0,0).  Il raggio delle curve di livello varia linearmente con la quota (se questa è compresa tra 0 e 3/π).      Dipendenza / indipendenza     Come si fa a capire dal grafico della distribuzione di U=(X,Y) se X e Y sono variabili casuali indipendenti o no?     Nel caso dell'istogramma di (Sesso,Settore) la riga di colonne che rappresenta la distribuzione dei maschi non ha andamento analogo a quella delle femmine, e questo ci fa capire che Sesso e Settore non sono indipendenti. Nel caso del lancio di due dadi, invece, tutte le righe di colonne hanno andamento simile (anzi, uguale): le uscite di primo e secondo dado sono indipendenti.  L'ipotesi di indipendenza corrisponde, nel caso finito (e nel caso sperimentale), alla proporzionalità tra le righe o tra le colonne della tabella a doppia entrata e, passando all'istogramma tridimensionale, corrisponde alla proporzionalità tra le altezze delle righe di colonnine o tra le altezze delle file di colonnine.     In generale, passando alle funzioni di densità al posto delle righe e delle file di colonnine si considerano le sezioni parallele al piano xz e le sezioni parellele al piano yz: due qualunque sezioni, ad esempio parallele al piano xz, devono essere ottenibili una dall'altra mediante una dilatazione/contrazione verticale. Nel caso delle funzioni densità dei due esempi inziali, dei proettili, ciò non accade mai: ad esempio la sezione determinata dal piano yz non ha lo stesso andamento (a meno di un fattore di scala) di nessuna delle altre sezioni ad essa parallela. Del resto è intuitivo che il valore di X e quello di Y sono tra loro condizionati: devono essere le coordinate di un punto che sta nel cerchio (X2+Y2 deve essere al più 1; se X è vicino ad 1 Y per forza deve essere vicino a 0).     Nel caso del sistema di variabili avente densità che ha per grafico un cono circolare retto, considerato sopra, X e Y sono indipendenti?  Evidentemente no, per le stesse motivazioni usate per le altre densità appena considerate.     Altri due esempi.     A destra è rappresentato un sistema (X,Y) con X e Y indipendenti: comunque sezioni la superficie con piani paralleli ai piani xz e yz ottengo grafici con andamenti simili: hanno massimo e punto di flesso collocati nella stessa posizione. Potrebbe avere una forma simile (anche se non centrata in (0,0) e con diverse unità su gli assi) la distribuzione di (X,Y) con X e Y altezze di un uomo e una donna sorteggiati a caso.     Invece, nel caso della superficie sotto a sinistra (per la quale a destra abbiamo tracciato un possibile grafico di dispersione sperimentale) siamo di fronte a X e Y non indipendenti; ad es., è evidente che le sezioni parallele al piano yz sono curve con il punto di massimo che man mano si sposta verso destra (avanza lungo la direzione dell'asse y).         Potrebbe avere una forma simile la distribuzione di (X,Y) con X e Y altezze di marito e moglie di una coppia sorteggiata a caso: l'altezza di uomini spostati con donne di una certa altezza ha andamento più o meno gaussiano, ma la loro altezza media è maggiore di quella degli uomini sposati con donne più basse (uomini più alti tendenzialmente sposano donne più alte: non è affatto vero che l'amore è cieco!).     Ma la dipendenza tra X e Y in questo ultimo caso è in un qualche senso "più forte" di quella che c'era tra X e Y nel caso dei proiettili: là avevamo che i valori che poteva assumere una delle due variabili era condizionato da quello che assumeva l'altra, qui abbiamo qualcosa di più: al crescere di X anche Y tende a crescere. Su questo aspetto ci si sofferma nella successiva voce "correlazione".     Sotto sono tracciate alcune curve di livello delle due ultimi superfici considerate. Nel primo caso sono ellissi simmetriche rispetto agli assi x e y, nel secondo hanno assi di simmetria obliqui, a conferma del fatto che al crescere dell'uscita X l'uscita di Y tende a crescere anch'essa.   Cenni alla sistemazione formale     Vediamo, a grandi linee, come precisare le considerazioni precedenti.     Consideriamo U = (X ,Y) con X e Y variabili casuali a valori in IR. Siano X e Y a valori negli intervalli, rispettivamente, I e J. U ha valori in I×J.     La legge di distribuzione di U è nota quando so calcolare i valori di una misura di probabilità Pr su tutti gli eventi del tipo U∈E×F con E e F sottointervalli di I e J:  Pr(U∈E×F) = Pr(X∈E and Y∈F).  Con la additività posso poi valutare Pr(U∈D) per altri domini D (cioè per altri insiemi ottenibili come "unioni numerabili di rettangolini").     I punti in cui cadono i proettili considerati nell'esempio iniziale sono esempi di variabili bidimensionali a valori in domini non rettangolari, ma può convenire considerarle definite in un rettangolo I×J, [−1,1]×[−1,1] o tutto R2: invece di considerare U a valori nel cerchio C posso considerare V tale che Pr(V∈E) =Pr(U∈E) se E è contenuto in C, Pr(V∈E)=0 se E è esterno a C.     La funzione di ripartizione f sarà: f(x,y) = Pr(X≤x AND Y≤y).     Se X e Y sono indipendenti, Pr(U∈E×F) = Pr(X∈E)·Pr(Y∈F) e f(x,y) = f1(x)·f2(y) (se f1 e f2 sono le funzioni di ripartizione di X e Y).         Nel caso discreto (X e Y variabili discrete) la legge di distribuzione è nota se so calcolare i valori della misura di probabilità Pr su tutti gli eventi del tipo U = (xi, yj) (xi: valori che può assumere X, yj: valori che può assumere Y).     In tal caso la legge di distribuzione è rappresentabile con un istogramma tridimensionale, come quello raffigurato all'inizio del paragrafo precedente, a sinistra.     Per estendere la definizione di probabilità al caso continuo dobbiamo estendere il concetto di integrale al caso bivariato.     Se f è una funzione positiva di due variabili definita su una superficie piana T che è continua, ossia, intuitivamente, che ha per grafico una superficie S di R³ senza tagli, ovvero che è tale che all'avvicinarsi di (x,y) ad un punto P f(x,y) tende a f(P), l'integrale di f su T è il volume del solido Q superiormente limitato da S e inferiormente da T e avente superficie laterale perpendicolare al piano x,y. Il volume di Q viene determinato come il limite del volume del solido formato da tanti parallelepipedi la cui unione tende a coincidere con Q. Approfondimenti puoi trovarli qui.     L'integrale di f su T viene indicato con la notazione  ∫∫T f.         Così come, nel caso univariato, abbiamo visto che (all'aumentare delle prove e all'infittirsi della partizione) l'istogramma sperimentale di una variabile continua U tende a stabilizzarsi sul grafico di una funzione f tale che Pr(c≤U≤d) è pari all'integrale di f tra c e d, così chiameremo continua una variabile bidimensionale per cui esista una funzione a 2 input f (funzione di densità) tale che, per ogni evento del tipo U∈E×F con E e F sottointervalli di I e J (se U varia in I×J):   ∫∫ E×F f  =  Pr(U ∈ E×F)     La superficie grafico di f approssima gli istogrammi sperimentali. Il volume del cilindro verticale avente per base il dominio T e limitato superiormente dal grafico di f è Pr(U∈T).  Ovviamente:     ∫∫ I×J f  =  1     Si ha che X e Y (continue) sono indipendenti sse f(x,y) = f1(x)·f2(y), dove f1 e f2 sono le funzioni di densità di X e Y. In altre parole, le sezioni con piani y=k sono tra loro scalate verticalmente (f(x,k) = f1(x)·f2(k)) e una cosa analoga accade per le sezioni con piani x=k. Nel caso discreto, si ha un istogramma tridimensionale le cui righe [colonne] di parallelepipedi sono istogrammi (bidimensionali) che sarebbero tra loro uguali se normalizzati.     Ciò traduce il fatto che comunque fissi X [Y], la variabile Y [X] si distribuisce sempre allo stesso modo, senza subire influenze.     Nel paragrafo precedente il primo grafico riprodotto è della funzione di densità di U=(X,Y) dove X e Y hanno densità gaussiana di media 0 e s.q.m. 1 e sono indipendenti. Le curve di livello sono cerchi con centro (0,0).     Comunque sezioni con piani paralleli ai piani xz e yz ottengo grafici ottenibili scalando verticalmente la gaussia di s.q.m. 1 e media 0. Le funzioni densità (vedi qui per il tracciamento dei grafici) sono: 2 2 2 2 x +y x y - ————— - ——— - ——— 1 2 1 2 1 2 f(x,y) = ——— e f1 (x) = ————— e f2 (y) = ————— e 2π √(2π) √(2π)     Anche la seconda funzione rappresentata graficamente nel precedente paragrafo è la densità di U=(X,Y) con X e Y aventi densità gaussiana di media 0 e s.q.m. 1, ma in questo caso X e Y non sono indipendenti; ad es., è evidente che le sezioni parallele al piano yz sono curve con il punto di massimo che man mano si sposta verso destra (avanza lungo la direzione dell'asse y). Le curve di livello in questo caso particolare sono ellissi aventi le bisettrici dei quadranti come assi di simmetria.     Gli integrali di funzioni di due variabili possono essere affrontati facilmente con WolframAlpha: per calcolare l'integrale per x ed y tra −∞ e ∞ della prima delle funzioni precedenti basta battere: integrate 1/(2*pi)*exp(-(x^2+y^2)/2) dx dy, x=-inf..inf, y=-inf..inf     Che cosa ottengo se batto quanto segue? sqrt(integrate 1/(2*pi)*exp(-(x^2+y^2)/2) dx dy, x=-1..1, y=-1..1)     Che cosa se batto quanto segue? integrate 1 dx dy, x=-1..1, y=-1..1 Esercizi:    Vedi qui per un uso di R impiegando la libreria source("http://macosa.dima.unige.it/r.R").  altri collegamenti     [nuova pagina]