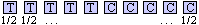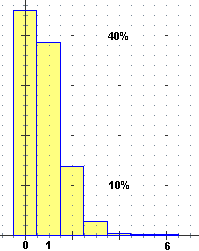Leggi di distribuzione (variabili discrete)
Il 
calcolo delle probabilità
studia situazioni in cui, accanto a condizioni che si riescono a valutare, intervengono fattori difficili da determinare che, per semplificare, si dicono essere
dovuti al caso.
Ad esempio se devo chiedere un'informazione per telefono e voglio valutare quanto mi costerà
la telefonata, posso tener conto che la tariffa prevede un costo fisso di CF cent. per chiamata e un costo di CS cent. per ogni
secondo di conversazione; i valori di CF e CS li posso conoscere a priori (mi basta consultare le condizioni del
contratto con la compagnia telefonica) mentre la durata della telefonata dipende da molti fattori (la persona che ha l'informazione risponde direttamente lei alla chiamata? quanto impiega a reperire l'informazione? con che
velocità parla? …).
Se T è il tempo in secondi per cui durerà la telefonata posso esprime il costo in centesimi col termine CF + CS · T (CostoFisso + CostoPerSecondo · TempoInSecondi) e, per esempio, l'evento che il costo superi 1 € posso esprimerlo con la formula CF + CS · T > 100.
In questa formula CF e CS sono variabili deterministiche, ossia variabili usuali, di cui
(note le condizioni del contratto) si può
determinare il valore; invece T è una variabile casuale : il suo valore può variare
in relazione a come, il "caso", fa evolvere l'evento.
T rappresenta una durata temporale, può assumere valori reali positivi qualunque. Nel caso del lancio di un dado la variabile U che esprime il numero uscito può assumere invece solo i valori 1, 2, 3, …, 6.
Variabili casuali che, come T, possono variare, con continuità, su tutto un intervallo di numeri reali
vengono dette variabili casuali continue, mentre quelle che, come U, possono assumere solo valori
"separati" l'uno dall'altro, elencabili in una successione, vengono dette variabili casuali discrete
("discretus", in latino, è il participio passato di "discernere", che significa "distinguere, separare").
In questa voce approfondiremo lo studio di queste ultime (clicca le immagini
per ingrandirle).
Esercizio (e soluzione)
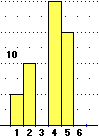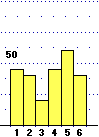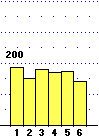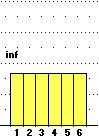
Istogrammi di distribuzione teorica di variabili casuali discrete
 |
A sinistra sono riprodotti gli istogrammi che rappresentano le leggi di distribuzione
dell'uscita U del lancio di  un dado equo
e di quella del lancio di
due dadi equi.
Come abbiamo visto, questi
sono gli istogrammi "limite" degli istogrammi sperimentali: le altezze delle colonne
non rappresentano più le frequenze sperimentali, ma (vedi figura a destra, riferita al lancio di un dado) i valori su cui
queste tendono a stabilizzarsi, ossia le probabilità (clicca le immagini per ingrandirle).
Nei casi, come questi, di una variabile discreta U che assume valori numerici interi, posso prendere come basi dei rettangolini che formano l'istogramma gli intervallini centrati sui numeri interi; in questo modo la probabilità che
U sia n è rappresentata sia dall'altezza del rettangolino con base centrata in n, sia dalla sua area, e l'area
dell'intero istogramma vale 100%, ossia 1. Nel primo caso ogni rettangolino è alto 1/6, nel secondo il rettangolino
che ha la base centrata nell'ascissa n ha altezza pari a Pr(U=n), ossia a (n-1)/36
se 2≤n≤7, a (12-(n-1))/36 se 7<n≤12.
|
 | |
 |
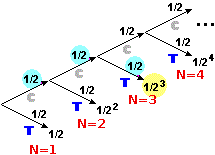
Consideriamo un esempio di variabile casuale discreta non finita :
il numero N dei lanci di una moneta equa da effettuare fino ad ottenere l'uscita di "testa" (T).
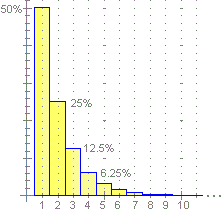
• Al 50% N=1, ossia viene T al primo lancio: Pr(N=1) = 1/2.
• Al secondo lancio ho metà della rimanente probabilità che venga T: Pr(N=2) = (1/2)/2 = 1/4 = 25%.
• La probabilità Pr(N=3) che T venga al terzo lancio è (vedi grafo a destra) (1/2)(1/2)(1/2)
= 1/23 = 1/8 = 12.5%.
• In generale: Pr(N = h) = 1/2h
A sinistra è tracciata parte dell'istogramma di distribuzione di N:
è un esempio di figura illimitata (la base dell'istogramma prosegue senza fine a destra) con area finita (uguale a 1). |
|  |
Media teorica
Nel caso di una distribuzione statistica di una variabile numerica, la media corrisponde, sull'istogramma,
alla ascissa del
centroide (o baricentro) di esso, cioè all'ascissa del punto per cui sospendere la base dell'istogramma
in modo che essa resti orizzontale. Anche nel caso dell'istogramma
di una legge di distribuzione teorica prendiamo questa ascissa come media teorica
della legge di distribuzione.
Ad esempio per l'uscita U del lancio di un dado equo la media teorica è 3.5:
infatti, trattandosi di un rettangolo, l'ascissa del baricentro deve stare a metà della base (vedi figura sotto
a sinistra). In analogia a quanto fatto per la media di una distribuzione
statistica, scriveremo M(U) = 3.5.
Esercizio (e soluzione)
|  |
|  |
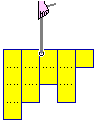
Nel caso di un
dado non equo, come quello costruito nel modo illustrato a destra, la media
sarà più vicina a 6 (la faccia più leggera, senza linguette incollate) che
ad 1 (la faccia più pesante, che difficilmente "esce").
Come possiamo calcolarla usando
la sua legge di distribuzione, rappresentata qui a sinistra dal suo istogramma (cliccalo per ingrandire)? |
 |
Nel caso statistico la media di una distribuzione X la possiamo ottenere (
Indici di posizione)
sommando i prodotti dei valori xk per le loro frequenze relative frk (corrispondenti alle aree delle colonne dell'istogramma sperimentale),
nel caso di una variabile casuale X che possa assumere N valori x1, …,xN faremo
analogamente la somma dei prodotti dei valori xk per le loro probabilità
Pr(X = xk) (corrispondenti alle aree delle colonne dell'istogramma teorico):
| M(X) = |
N | (xk· frk) |
| Σ |
| k = 1 |
|
diventa: |
| M(X) = |
N | (xk· Pr(X = xk)) |
| Σ |
| k = 1 |
|
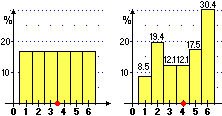
Dunque, per il dado non equo ho:
M(U) = (8.5%·1+19.4%·2+12.1%·3+12.1%·4+17.5%·5+30.4%·6) =
(8.5·1+19.4·2+12.1·3+12.1·4+17.5·5+30.4·6)/100 = 4.019 = 4.02 [arrotondando
a 3 cifre]
La media di una variabile casuale X a volte viene chiamata anche speranza matematica o valore atteso
("expected value" in inglese) di X, e indicata E(X). Nonostante l'aggettivo "atteso" non è detto
che si tratti di un valore che la variabile casuale può assumere: nei due casi appena considerati
abbiamo ottenuto come medie delle uscite di un dado in un caso 3.5 e nell'altro 4.02, valori
che, ovviamente, non possono uscire. E, come si vede dal secondo esempio, non è detto neanche che sia vicino al valore più
probabile (ossia alla moda).
Qual è la media nel caso del numero N dei lanci da effettuare per ottenere testa considerato sopra?
| 1/2 |
+2·1/(22) |
+3·1/(23) |
+4·1/(24) |
+5·1/(25) |
... |
+10·1/(210) | +... = 2 |
| 1/2 | 1 | 1.375 | 1.625 | 1.78125 |
... | 1.98828125 |
M(N) = 2. Se appendessimo un "ipotetico" istogramma di cartoncino
di dimensioni infinite come quello di N per un forellino praticato in corrispondenza
dell'ascissa 2, esso starebbe in equilibrio.
Nota. In questo esempio l'ultimo "..." sta ad indicare che la somma può
proseguire all'infinito. È un'estensione del concetto di somma che, anche se implicitamente, abbiamo già
incontrato più volte. Ad esempio la scrittura 1.111…, ad intendere che il numero prosegue con una successione infinita
di "1", potrebbe essere sostituita da 1+1/10+1/100+1/1000+…. In questo caso si tratta di una somma che, calcolandola
per un numero di addendi via via crescente, si avvicina sempre più ad un numero, appunto a 1+1/10+1/100+1/1000+…,
che in questo caso potremmo scrivere anche in forma finita: 1+1/9; infatti 1/9 = 0.111….
Per un esempio analogo
( i numeri),
1.999… = 1+9/10+9/100+9/1000+… = 2.
Ovviamente, non in tutti i casi una "somma infinita" è uguale ad un numero. Ad esempio 1+2+3+4+…,
all'aumentare del numero di interi che aggiungo, cresce oltre ogni limite.
È chiaro come, in casi simili a quelli richiamati negli esempi iniziali, si possono
usare scritture come
∑ k = 0 … ∞ 1/10k,
1 + ∑ k = 1 … ∞ 9/10k, …,
in cui l'uso di ∑ ( indici di posiz. e dispers.)
viene esteso al caso di una somma di infiniti addendi.
Nel caso di tutte le leggi di distribuzione ad uscite in un insieme infinito a1, a2,
a3, … abbiamo a che fare con una somma infinita di probabilità che vale 1; ad es.
nel caso del lancio della moneta
abbiamo che
∑ k = 1 … ∞ 1/2k = 1/2+1/4+1/8+1/16+… = 1.
Nel caso dell'uscita U del lancio di due dadi equi
l'istogramma di distribuzione di U ha forma simmetrica rispetto alla retta di ascissa 7: quindi la media è M(U) = 7.
Osserviamo che le distribuzioni U1 e U2 delle uscite dei due singoli dadi hanno media M(U1) = M(U2) = 3.5, e 7 = 3.5+3.5.
In effetti potevamo dedurre che M(U) = 7 da una proprietà più generale:
se X e Y sono due variabili casuali numeriche aventi medie
M(X) e M(Y), la variabile casuale X+Y ha media
M(X+Y) = M(X)+M(Y).
Questa proprietà vale sia nel caso sperimentale che
in quello teorico, ed è abbastanza evidente; si pensi ad un esperimento con n prove:
M(X+Y) = ((x1+y1)+...+(xn+yn)) / n =
(x1+...+xn)/n +
(y1+...+yn)/n = M(X) + M(Y)
Data una variabile casuale numerica X diciamo che
la media dei valori assunti da X in un certo numero n di "prove" è una
media sperimentale (o media empirica o media statistica)
di X. A volte questo numero viene indicato con Mn(X).
Ad esempio se U è l'uscita di un dado e faccio
20 lanci, la media dei valori così ottenuti è una media sperimentale di U e posso indicarla con
M20(U) (tenendo presente, però, che se ripeto i 20 lanci potrei
ottenere una media diversa).
Se chiamo T la tabellina che associa ad 1,
2, 3, …, 6 le rispettive frequenze ottenute con queste 20 prove, T è una distribuzione statistica (ai valori sono associate le frequenze invece delle probabilità) la cui media
non è altro che uno dei possibili valori che (in un esperimento di lancio dei dadi) può assumere la media sperimentale di U considerata sopra: M20(U) = M(T).
Osserviamo che il simbolo M(…) viene usato indifferentemente per le medie "teoriche" e per le medie "sperimentali": dal contesto si comprende quale interpretazione darne,
ossia quando M(X) è riferito a una variabile casuale X o a una distribuzione statistica X.
Mediana e varianza teorica
In modo del tutto analogo avviene il passaggio dalla
varianza sperimentale a quella teorica,
sostituendo le probabilità alle frequenze relative.
Considerazioni analoghe valgono per la
mediana.
Per esemplificare il calcolo esaminiamo la variabile casuale U = "uscita del lancio di un dado equo".
• La mediana è un valore u tale che, nel caso sperimentale,
ha al più il 50% di uscite minori di esso e al più il 50% maggiori; nel caso teorico
la condizione diventa: Pr(U < u) ≤ 1/2
e Pr(U > u) ≤ 1/2. Di valori di tal genere, nel caso del dado, ne abbiamo
due, sia 3 che 4; ciò corrisponde al fatto che (vedi ) la retta verticale che taglia a metà
l'area dell'istogramma passa per l'ascissa 3.5. Se assumiamo la convenzione di scegliere il
primo valore per cui ciò si verifica, diremo che la mediana è 3.
• Calcoliamo la varianza: V(U) = M((U-M(U))2 =
"media dei quadrati degli scarti dalla media":
((1-3.5)2+(2-3.5)2+(3-3.5)2+(4-3.5)2+(5-3.5)2+(6-3.5)2)/6 =
(2·2.52+2·1.52+2·0.52)/6 =
35/12.
Quindi lo scarto quadratico medio è σ(U) = √(35/12) = 1.7078251.
Nel caso del dado non equo la mediana è 4 in quanto:
Pr(U < 4) = 8.5%+19.4%+12.1% = 40%
Pr(U > 4) = 30.4%+17.5% = 47.9%
Nota. Per la rappresentazioni grafiche delle leggi di distribuzione e per
il calcolo di medie e varianze puoi usare R.
Qui trovi come studiare
la distribuzione del "dado non equo" considerata sopra.
Nel caso dell'uscita U del lancio di due dadi equi, qual è la varianza?
Anche per la varianza si ha:
Var(X+Y) = Var(X)+Var(Y). Nel nostro caso:
Var(U1+U2) = Var(U1)+Var(U2) = 35/12 + 35/12 = 35/6.
Questa proprietà vale, però, se X e Y sono indipendenti, non in generale.
Si pensi, come "controesempio", al caso in cui X sia
il numero sulla faccia superiore di un dado equo e Y sia quello sulla faccia inferiore. Se lancio il dado sia X che Y di distribuiscono uniformemente,
con media 3.5 e varianza 35/12. Le facce opposte di un dado hanno numeri
che sommati danno 7, per cui X+Y vale sempre 7. La media è dunque 7,
in accordo col fatto che 3.5+3.5=7, ma la varianza è 0 in quanto
X+Y ha valore costante.
Non dimostriamo questa proprietà. Possiamo controllarla sperimentalmente con R
mediante i comandi a cui puoi accedere da qui
(o con questo script; esamina il codice
sorgente per vedere come è realizzato; lo script è riferito al caso dei due dadi equi; puoi modificarlo per studiare altre leggi).
Analogamente si può controllare sperimentalmente che se X e Y sono indipendenti vale anche M(X·Y) = M(X)·M(Y). Se si pensa alla
definizione di indipendenza la cosa non sorprende.
La distribuzione binomiale
Consideriamo una situazione abbastanza simile a quella delle successive alzate di un mazzo di carte ( dipendenza e indipendenza):
lanciamo una moneta equa 10 volte;
qual è la legge di distribuzione della
variabile casuale:
N = "n° di teste uscite"?
Sembra un problema stupido, ma vedremo che è il punto di partenza per
affrontare problemi più significativi, come:
un forno automatico
produce mediamente 1 biscotto bruciacchiato ogni 8, e i biscotti sono successivamente mescolati e impacchettati
automaticamente
in confezioni da 6,
• qual è la probabilità
che in una confezione non vi siano biscotti bruciacchiati,
o che ve ne sia 1, …, o che siano tutti bruciacchiati?,
• cioè qual è la legge di distribuzione della
variabile casuale N = "n° di biscotti bruciacchiati in una confezione" ?
Proviamo prima a studiare il problema con una simulazione.
L'idea è generare 10 volte un numero a caso equamente distribuito tra 0 e 1, pensando 0 come "croce" e 1 come "testa",
e prendere come N la somma di questi 10 numeri; infatti tale somma è uguale a numero delle volte che
è uscito 1, cioè "testa".
Ecco qua sotto l'analisi (mediante il programma R)
degli esiti di una tale simulazione:
n <- 10000; dati <- NULL; for (i in 1:n) dati[i]=sum(floor(runif(10)*2))
hist(dati, seq(-1/2, 10.5, 1), probability=TRUE, col="yellow")
abline(h=seq(0.05,0.25,0.05),lty=3)
summary(dati)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.000 4.000 5.000 4.982 6.000 10.000
dev.new()
boxplot(dati,horizontal=TRUE, col="yellow", range=0)
# la visulizzazione sul boxplot del 5° e del 95° percentile:
points(quantile(dati,0.05),1,pch=20); points(quantile(dati,0.95),1,pch=20)
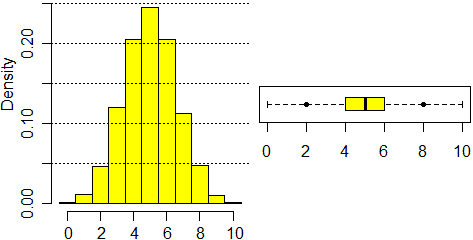
Effettuiamo, ora, lo studio teorico.
Dobbiamo trovare i valori di Pr(N=0), Pr(N=1), ..., Pr(N=10).
Iniziamo a considerare, per es., Pr(N=5).
|
• Valutiamo la probabilità che testa esca esattamente nei primi 5 lanci (vedi figura a lato).
La probabilità che esca T in un lancio è 1/2, la stessa che esca C. Poiché i dieci lanci sono indipendenti, posso moltiplicare le probabilità. Ottengo che
la probabilità cercata è (1/2)·(1/2)·...·(1/2) = (1/2)10, cioè 2–10. |
 |
|
• Ottengo lo stesso valore per la probabilità che testa esca nei lanci tra il 2° e il 6° (vedi figura a lato), e per qualunque altra collocazione dei 5 lanci in cui esce testa. |
 |
|
• I modi in cui posso scegliere i 5 posti sono C(10,5), dove C(n,k) indica quante sono le combinazioni di n elementi k a k, cioè la quantità dei sottoinsiemi di k elementi di un insieme di n elementi
( calcolo combinatorio). |
|
• C(10,5) =
10/5 · 9/4 · 8/3 · 7/2 · 6/1 = 9·4·7 |
|
• Quindi, la probabilità cercata, per la proprietà additiva, è la somma di C(10,5) termini uguali a 2–10: |
|
Pr(N=5) = C(10,5) · 2-10 = 9·4·7 / 210 = 24.6% |
| In generale: |
Pr(N = i) = C(10, i) / 210 (i = 0, 1, …, 10) | |
Per controllare il nostro ragionamento
teorico confrontiamoci con gli esiti della simulazione: dall'istogramma sperimentale
abbiamo, ad es., Pr(N=5) = 24% e Pr(N=3) =12%; con la formula
trovata per Pr(N=5) abbiamo ottenuto 24.6%; per Pr(N=3) abbiamo
C(10,3) / 210 = 10/3·9/2·8/1 / 210 = 15 / 27 = 11.7%. In entrambi i casi abbiamo un buon accordo.
Se lanciassi n volte la moneta avrei, del tutto analogamente:
Pr(N = i) = C(n, i) / 2n (i = 0, 1, …, n)
È un caso particolare di legge di distribuzione binomiale,
discussa più in generale tra un paio di paragrafi. Il nome deriva dalla presenza del
coefficiente binomiale C(n,i).
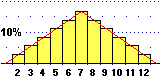
Ecco l'istogramma di distribuzione teorico nel caso n = 10, che coincide con quello sperimentale nel caso in cui
T sia uscita in k lanci esattamente C(n,k) volte:
1 volta 0 teste, 10 volte 1 testa, 45 volte 2 teste, ..., 210 volte 4 teste, 252 volte 5 teste, 210 volte 6 teste,
..., 10 volte 9 teste, 1 volta 10 teste. L'istogramma ha un asse di simmetria verticale,
così come il
triangolo di Tartaglia.
 |
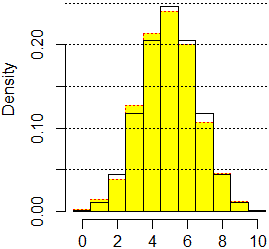L'istogramma teorico realizzato con
R ("choose" calcola il nostro "C") e
(tratteggiato e di colore giallo) quello
sperimentale relativo a 2000 lanci.
"var" è la varianza. |
n <- 2000; dati <- NULL; for (i in 1:n) dati[i]=sum(floor(runif(10)*2))
hist(dati, seq(-1/2, 10.5, 1), probability=TRUE, col="yellow", border="red", lty=3)
dati2 <- NULL; for (i in 0:10) dati2 <- c(dati2,rep(i,choose(10,i)))
hist(dati2, seq(-1/2, 10.5, 1), probability=TRUE, add=TRUE)
abline(h=seq(0.05,0.25,0.05),lty=3)
var <- sum( (dati2-mean(dati2))^2 ) / length(dati2); var
2.5
|
L'elaborazione è stata realizzata al computer, come la seguente, per n = 9:
 |
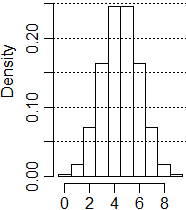dati3 <- rep(0,choose(9,0))
for (i in 1:9) dati3 <- c(dati3,rep(i,choose(9,i)))
hist(dati3, seq(-1/2, 9.5, 1), probability=TRUE)
abline(h=seq(0.05,0.25,0.05),lty=3)
var <- sum( (dati3-mean(dati3))^2 ) / length(dati3); var
2.25 |
La media, per simmetria, è evidentemente n/2. È naturale congetturare, da questi esempi in cui i calcoli sono stati effettuati dal computer, che la varianza sia n/4 (ho ottenuto 2.5 per n=10, 2.25 per n=9) e che, quindi, lo
scarto quadratico medio sia σ = √n/2. La cosa può essere effettivamente dimostrata:
• N = u1 + u2 + ... + un dove
per tutti gli u k si ha u k=1 se al primo lancio è uscita T, u k=0 altrimenti.
• i lanci sono indipendenti, quindi la "varianza della somma è la somma delle varianze";
• M(u k) = 1/2; Var(u k) = 1/2 (0-1/2)2 + 1/2 (1-1/2)2 = 1/4; ...
• Var(N) = Var(u1) + ... + Var(un) = 1/4·n = n/4
Torniamo all'esempio del forno,
così sintetizzabile:
se un forno
produce mediamente 1 biscotto bruciacchiato ogni 8, qual è la legge di distribuzione della
variabile casuale
N = "n° di biscotti bruciacchiati in una confezione da 6".
Ragioniamo in modo simile a quanto fatto nel caso delle monete.
Sia N la variabile casuale a valori in {0, 1, ..., 6} che rappresenta il numero di biscotti difettosi.
È sensato ritenere (dato il rimescolamento presente prima del confezionamento) che le estrazioni dei biscotti siano una indipendente dall'altra. Quindi la probabilità che esattamente i primi k biscotti estratti siano difettosi è data dal prodotto:
(1/8)·(1/8)· … ·(1/8)·(7/8)· … ·(7/8) = (1/8)k·(7/8)6-k.
 |
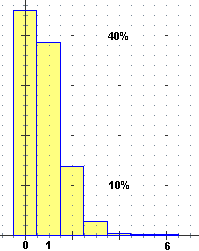Poiché non ci interessa la disposizione dei biscotti difettosi, abbiamo:
Pr(N=k) = C(6,k)·(1/8)k·(7/8)6–k. |
| Ecco, a sinistra e sotto, elaborazioni grafiche e calcoli effettuati con l'ausilio del computer: |
media: 0.75 mediana = 0.6331092204
moda: [-0.5,0.5)
freq.rel.massima: 44.8795%
varianza = 0.65625
|
Qual è la probabilità che una confezione presenti biscotti bruciacchiati?
Trovare la probabilità che vi sia almeno
un biscotto difettoso vuol dire
calcolare Pr(N > 0), che
(per la proprietà additiva) equivale a
100% – Pr(N = 0):
1 – C(6,0)·(1/8)0·(7/8)6
= 1 – 1·1·(7/8)10 = 1 – 0.4487953... = 55.1% [valore arrotondato]
Generalizzando dal caso di una confezione da 6 ad una da n biscotti, dal caso della difettosità con probabilità di 1/8 a quello della difettosità con probabilità p, abbiamo che la probabilità che in una confezione vi siano k biscotti difettosi è:
Pr(N = k) = C(n, k) · pk · (1 – p)n–k
Anche questa legge di distribuzione, che generalizza quella considerata nel caso delle monete eque, viene chiamata legge di distribuzione binomiale (o di Bernoulli).
Si applica a tutte le situazioni in cui si ripete n volte la prova su una variabile casuale che può assumere solo due valori, in cui p è la probabilità di uno di questi due valori e N è il numero delle volte in cui questo valore esce.
Possiamo osservare, come già fatto per le monete, che N è interpretabile come
∑ in= 1 X i
con X i a valori in {0,1} e distribuzione: Pr(X i=1) = p,
Pr(X i=0) = 1–p. Da qui,
tenendo conto che
• M(X i) = Pr(X i =0)·0+Pr(X i =1)·1 = (1–p)·0+p·1 = p
e
• Var(X i) = Pr(X i =0)·(0–p)2+Pr(X i =1)·(1–p)2 = (1–p)p2+p(1–p)2 = p(1–p)
abbiamo (vedi):
M(N) = M(Σ i X i) = Σ i M(X i) = p + … + p = np e (vedi):
Var(N) = Var(Σ i X i) = Σ i Var(X i) = p(1-p) + … + p(1-p) = np(1–p).
 |
Nel caso dei biscotti:
M(N) = 6·1/8 = 3/4, Var(N) = 6·1/8·7/8 = 21/32 = 0.65625,
in accordo coi valori calcolati direttamente sopra.
A lato la rappresentazione grafica di due leggi binomiali.
Si noti che in entrambi i casi la media, np, differisce per meno di un'unità
dalla moda (in un caso differisce di 0.6, nell'altro di 0.4).
Si può dimostrare che
questo accade in generale, per ogni n naturale e per ogni p in (0,1).
|
| Esercizio (e soluzione) |
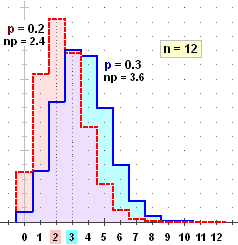
Il grafico della legge binomiale Bn, p di ordine n e "probabilità di successo nella singola prova" p quando n è molto grande, è pressoché simmetrico rispetto alla retta verticale che ha per ascissa la media, anche se p ≠ 1/2.
A lato sono raffigurati per p = 0.2 i casi n = 50, 20, 10 (i punti che rappresentano P(N=k) per k alto hanno ordinata trascurabile rispetto al punto modale, per cui appaiono confusi con l'asse orizzontale).
Più n è piccolo, più è evidente la asimmetria, con una "coda" verso destra.
|
 |
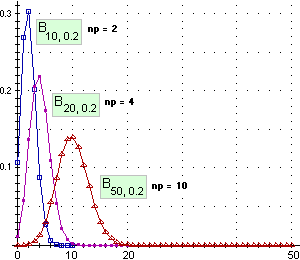| I grafici realizzati con R: |
n <- 10; plot(0:n,dbinom(0:n,n,0.2),type="h", lwd=3)
dev.new(); n <- 20; plot(0:n,dbinom(0:n,n,0.2),type="h", lwd=3)
dev.new(); n <- 50; plot(0:n,dbinom(0:n,n,0.2),type="h", lwd=3) |
 |
Nelle situazioni in cui n è molto grande (si pensi a un problema di "pezzi difettosi", come quello dei biscotti, nel caso si debba
valutarne la presenza in una partita di 1000 pezzi), il calcolo dei
coefficienti binomiali diventa molto complicato.
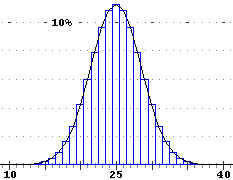
Vedremo, in una voce successiva [ limiti in probabilità], che all'aumentare di n i grafici delle leggi binomiali tendono a stabilizzarsi sul grafico di una funzione rappresentata da una formula determinabile a partire da n e p. Questo semplificherà notevolmente lo studio di tali situazioni. A lato il caso di B50,1/2, da cui si capisce che tale funzione avrà grafico simmetrico rispetto alla retta verticale
avente come ascissa il valor medio. |
Nota. Il 
programma R (in ogni sistema
operativo) ti consente di calcolare e
rappresentare graficamente leggi di distribuzione binomiali (qui trovi come studiare
la distribuzione del "n° di biscotti bruciacchiati per confezione" considerata sopra)
Nell'esercizio 3.13, presente tra gli "altri esercizi" a cui puoi accedere da qui sotto, sono illustrati significato ed uso della legge
di distribuzione multinomiale, che generalizza la legge binomiale.
Vedi qui per un uso di R impiegando la libreria
source("http://macosa.dima.unige.it/r.R").
Altri esercizi:
altri collegamenti [nuova pagina]
