Indici di posizione e di dispersione

  Indici di posizione

Data una sequenza di informazioni di tipo numerico, eventualmente già classificate sotto forma di distribuzione statistica, i suoi valori medi (media, moda e mediana) vengono chiamati anche indici di posizione in quanto indicano, con diverse caratterizzazioni, la zona dell'asse numerico in cui tali dati cadono con maggiore frequenza.
    Abbiamo già osservato che il confronto tra i diversi indici di posizione può dare anche indicazioni sulla forma dell'istogramma di distribuzione.   Ad esempio affinché la rappresentazione grafica sia simmetrica rispetto a un asse verticale è necessario (non sufficiente) che media e mediana coincidano.   Invece se la rappresentazione grafica è più o meno a forma di campana ma allungata verso destra [sinistra], la media è maggiore [minore] della mediana.
    Una interpretazione fisica del fenomeno è che la mediana rappresenta l'ascissa in cui praticare un taglio verticale che divida l'istogramma in due parti di area uguale, mentre la media è l'ascissa del baricentro dell'istogramma, ossia del punto dell'asse orizzontale per cui appenderlo in modo che, capovolto, rimanga con la base orizzontale.
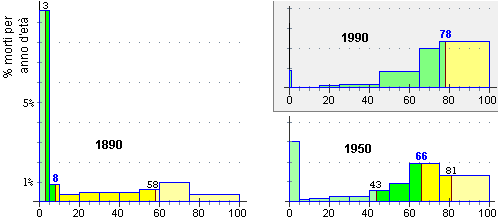
    Nella figura riprodotta nel punto successivo sono rappresentate le distribuzioni delle età dei morti in Italia nel 1890, nel 1950 e nel 1990. Chiamiamole, in ordine, Età1890, Età1950 ed Età1990.
    Le rispettive medie sono 28, 58 e 75: un morto nel 1890 aveva mediamente 28 anni, 58 nel 1950 e 75 nel 1990.  Usando M per indicare la media:
M(Età1890) = 28, M(Età1950) = 58 e M(Età1990) = 75.
    Le età mediane di morte erano invece, in ordine, 8, 66 e 78:
Mediana(Età1890) = 8, Mediana(Età1950) = 66 e Mediana(Età1990) = 78.
    Il fatto che, nel 1890, la media abbia un valore molto maggiore della mediana (mascherando in parte il fenomeno della mortalità infantile) è dovuto alla lunga coda destra che fa aumentare il risultato del calcolo della media. Nel 1990, invece, la media è inferiore alla mediana a causa della coda sinistra; la differenza in questo caso è lieve in quanto si tratta di una coda molto "sottile", e quindi non incide molto sul risultato.

  Indici di dispersione

Sono chiamati indici di dispersione degli indicatori numerici che danno un'idea quantitativa di come i dati sono più o meno sparpagliati. Per introdurli facciamo riferimento alle distribuzioni Età1890, Età1950 ed Età1990 considerate nel paragrafo precedente e rappresentate qua sotto (clicca le immagini per ingrandirle).

 distribuzione dell'età dei morti in Italia in vari anni

Passando dal 1890 al 1950, oltre a uno spostamento verso destra della zona in cui si concentrano le età di morte (testimoniato dall'aumento sia della media che della mediana: punto precedente), possiamo osservare un maggiore addensamento dei dati: l'istogramma assume una forma più tozza.
    Questa percezione intuitiva può essere precisata considerando l'intervallo in cui si colloca il 50% centrale dei dati, ossia i dati che vanno dal 25° al 75° percentile, che per il 1890 sono circa 3 e 58 (il 25% dei morti aveva età che non superava i 3 anni e il 75% età che non superava i 58 anni), e per il 1950 sono circa 43 e 81. Questi valori sono stati evidenziati anche sugli istogrammi.
    Abbiamo visto che la rappresentazione di questi intervalli fa parte dei box-plot:

1890   1950

<------------ 55 -----------> 0 3 8 58 100 ||==|=========================|--------------|------- / `mediana \ 25° per- 75° per- centile centile <------- 38 ------> 0 43 66 81 100 -|---------------------|==========|=======|-------|-- / mediana \ 25° per- 75° per- centile centile

La ampiezza di questo intervallo, che viene chiamata distanza interquartile in quanto costituisce la distanza tra il valore che delimita il primo quarto dei dati da quello che ne delimita l'ultimo quarto, passa da 55 a 38.  Per il 1990 si ha un'ulteriore riduzione della dispersione: si può calcolare che questa distanza diventa 32.
    La distanza interquartile, indicato in genere con IQR (InterQuartile Range), è l'indice di dispersione d'uso più generale.

Vedi qui come ottenere grafici simili ai precedenti.

  Altri modi per valutare la dispersione di una sequenza di N dati x₁, x₂, … x_N si basano sull'idea di quantificare in qualche modo il loro livello di concentrazione attorno a un indice di posizione p.
    Una prima possibilità è quella di fare la media delle distanze dei singoli dati da p:

scarto assoluto medio da p =	|x1– p| + |x2– p| + … |xN– p|
	————————————
	N

Il nome deriva dal fatto che con scarto di x da p si intende la differenza x–p. Lo scarto è positivo se x>p, negativo se x<p, nullo se x=p.  Un esempio di scarto è l'errore di approssimazione, ossia lo scarto del valore approssimato dal valore esatto.  Al posto di "scarto" si usa spesso, con lo stesso significato, la parola deviazione.
[ Facciamo la media delle distanze, ossia dei valori assoluti degli scarti, e non quella degli scarti, in quanto altrimenti scarti positivi e negativi si compenserebbero tra loro, dando luogo a una sottostima della dispersione ]

    Esaminiamolo nel caso dei seguenti dati:  13, 15, 18, 22, 25,  riferito alla mediana (= 18).
scarto assoluto medio dalla mediana = (5 + 3 + 0 + 4 + 7)/5 = 19/5 = 38/10 = 3.8
    La IQR in questo caso sarebbe stata 22 – 15 = 7. Si può osservare che lo scarto assoluto medio dalla mediana è quasi uguale alla semidistanza interquartile.

E se calcolassimo lo scarto assoluto medio non dalla mediana ma dalla media o da un altro ipotetico indice di posizione p?
La figura a fianco rappresenta graficamente i valori che assume la somma degli scarti assoluti da p al variare di p nel caso dei dati considerati due paragrafi sopra. Lo scarto assoluto medio ha lo stesso andamento (è ottenuto dividendo per il numero dei dati).     Si tratta di una funzione continua lineare a tratti, ossia avente per grafico una spezzata. [ È continua in quanto ottenuta sommando e componendo funzioni continue; è costituita da tratti lineari in quanto in ciascuno dei vari intervalli  – (-∞,13], [13,15], … [25,∞) –  è la somma di funzioni polinomiali di primo grado in p  – 13-p o -(13-p), 15-p o -(15-p), … –  e quindi è anch'essa una funzione polinomiale di primo grado o una costante ] Dal grafico osserviamo che la sommma degli scarti assoluti, e quindi lo scarto assoluto medio, è minimo per p = 18, che è la mediana dei nostri dati.
La cosa può essere dimostrata in generale: la mediana è il valore rispetto a cui lo scarto assoluto medio è minimo. Quindi ha senso considerare lo scarto medio assoluto dalla mediana come indice della dispersione dei dati attorno alla mediana.

Cerchiamo un indice per quantificare la dispersione dei dati attorno alle media, ossia che sia minimo se calcolato rispetto alla media. Al posto dei valori assoluti degli scarti, che provocano la presenza dei "punti angololosi" nel grafico considerato sopra, e fanno sì che esso abbia punti di minima ordinata solo in corrispondenza di qualche dato, consideriamo i loro quadrati.
La figura a fianco rappresenta graficamente i valori che assume la somma dei quadrati degli scarti p al variare di p nel caso dei dati considerati sopra, che hanno come media (13+15+18+22+25)/5 = 93/5 = 186/10 = 18.6.     Si tratta di una funzione polinomiale di 2° grado, con grafico parabolico.     Dal grafico osserviamo che assume valore minimo proprio quando p è uguale alla media.
La cosa è facilmente dimostrabile:  sviluppando i quadrati si ottiene (13²+15²+…+25²) – 2(13+15+…+25)p + 5p² che graficamente corrisponde a una parbola con vertice (13+15+…+25)/5 [ derivata o funz.polinomiali].

    In generale: la media è il valore rispetto a cui la somma dei quadrati degli scarti è minima. Quindi potremmo considerare questo valore, diviso per il numero dei dati, come un indice della dispersione dei dati attorno alla media. Per N dati x₁,…,x_N di media μ ("μ" è la lettera greca "mu", o "mi"), si dà, quindi, la seguente definizione:

varianza =	(x1– μ)2 + (x2– μ)2 + … (xN– μ)2
	——————————————
	N

La varianza è quindi la media dei "quadrati" degli scarti dalla media. Per ottenere un valore con ordine di grandezza confrontabile con quello degli scarti dobbiamo applicare alla varianza la "radice quadrata", ossia considerare:

scarto quadratico medio = √varianza = (	(x1– μ)2 + (x2– μ)2 + … (xN– μ)2	)	1/2
	———————————————
	N

Si noti che il termine "scarto quadratico medio" (s.q.m.), nonostante il nome, non indica la media degli scarti al quadrato (che è chiamata "varianza"), ma la loro radice quadrata. Al posto di esso si usa spesso deviazione standard o scarto standard, ma, come vedremo (alla voce Limiti in probabilità), questi termini sono usati anche per indicare un valore leggermente diverso.  Spesso viene rappresentato col simbolo σ (la lettera greca "sigma"). La varianza è invece indicata con Var (o V).
    Concludendo, come indice della dispersione dei dati attorno alla media in genere si usa il loro scarto quadratico medio da essa.

  Provo a calcolare σ (Età1950) procedendo in modo simile a quanto fatto sopra per lo scarto assoluto medio dalla mediana e tenendo conto che M(Età1950) = 58:

√	(58–2.5)2·729 + (58–7.5)2·35 + (58–15)2·77 + … + (58–87.5)2·1569	= 29.64… = 30
	—————————————————————————
	4819

    Analogamente per le età dei morti nel 1890 (che hanno 25 come media) ottengo σ(Età1890)=31.  Lo s.q.m. in questo caso non evidenzia bene (come lo fa invece la distanza interquartile) la diversa dispersione che c'è nei due anni.  È bene tener presente che si tratta di un indice di dispersione rispetto alla media, che ha senso usare se riferito a questa.

  Notazioni e proprietà di M e Var

Il simbolo Σ (detto sommatoria e costituito dalla lettera maiuscola greca "sigma") viene utilizzato per descrivere in modo compatto una somma di molti termini contenenti variabili indiciate o dipendenti da un parametro a valori interi. Ecco un paio di esempi:

Lunghezza(P0P1…Pn) =  n – 1 d(Pi Pi+1)   Σ i = 0		definisce la lunghezza della poligonale P0P1…Pn come la somma delle distanze:  d(P0P1)+d(P1P2)+…+d(Pn-1 Pn)
10 n2 = 385   Σ n = 1	si legge "la somma di n2 per n da 1 a 10 è uguale a 385" e abbrevia la scrittura: 12+22+32+42+52+62+72+82+92+102 = 385

Nota. Per comodità di scrittura a volte si usano notazioni più compatte. Ad esempio nell'ultimo caso si usa l'espressione a lato, a sinistra o, se è chiaro dal contesto quali siano il valore iniziale e quello finale dell'indice n, quella, più breve, a destra.	∑ n = 1..10 n2       ∑ n n2
Ecco come fare il calcolo precedente con R: a <- function(n) n^2    # a(n) elemento n-esimo della sommatoria S <- function(n) sum(a(1:n)); S(10)  # somma a(1)+...a(10)

    Se la distribuzione X ha x₁,…,x_N come valori (centrali delle classi) e f₁,…,f_N come corrispondenti frequenze, il totale dei dati è f₁+…+f_N, e la sua media M(X) può essere descritta con:

M(X) =  N (xk· fk)  /  N fk Σ Σ k = 1 k = 1

o con:

M(X) =  N (xk· frk) Σ k = 1

se fr_k indica la frequenza relativa del valore x_k:  fr_k = f_k / Totale,  Totale = Σ_k f_k.
•  Ad es. se so che in un cinema il 70% degli spettatori sono ragazzi che hanno pagato 3 € e il 30% sono adulti che hanno pagato 5 €, posso dire che mediamente uno spettatore ha pagato:  3·70%+5·30% = 3·0.7+5·0.3 = 2.1+1.5 = 3.6 €.
  Calcoli con R: x <- c(3,5); fr <- c(70,30)/100; sum(x*fr)

•  Nel caso di Età1950, se disponessi delle frequenze percentuali invece che di quelle assolute:
 [0,5): 15.1%;   [5,10): 0.7%;   [10,20): 1.6%;   [20,30): 2.7%;   [30,40): 2.8%;
 [40,50): 5.9%;   [50,60): 9.5%;   [60,75): 29.1%;   [75,100): 32.6%
potrei fare:   M(Età1950) = 2.5·0.151 + 7.5·0.007 + 15·0.016 + 25·0.027 + 35·0.028 + 45· 0.059 + 55·0.095 + 67.5·0.291 + 87.5·0.326  =  58.3725 (da arrotondare a 58).

  Quando è chiaro dal contesto quali siano i valori tra cui deve variare l'indice della sommatoria (cioè la "i" nel primo degli esempi precedenti, la "n" nel secondo e la "k" nei rimanenti) si può fare a meno di indicarli.  Nel caso della media, ad es., si potrebbe scrivere:
M(X) = Σ_k (x_k·fr_k)   sottointendendo la somma va estesa a tutti i valori x_k della distribuzione.
    Un'altra possibiltà è  Σ_kJ (x_k·fr_k)  avendo specificato che J = {1, 2, 3, …, N}.
    Si noti che l'indice di una sommatoria è una variabile locale (o muta): potrei usare al suo posto una qualunque altra variabile (a patto che non compaia già all'interno della sommatoria con altro significato).

  Se X è una distribuzione e k è un valore costante diversa da 0, con X+k, X-k, kX e X/k possiamo indicare le distribuzioni aventi i valori, rispettivamente, aumentati, diminuiti, moltiplicati o divisi per k, e le stesse frequenze di X.  Ad esempio se X è la distribuzione:
   980 con frequenza 3, 990 con freq. 5, 1010 con freq. 7, 1030 con freq. 5,
posso indicare con X-1000 la distribuzione:
    -20 con freq. 3, -10 con freq. 5, 10 con freq. 7, 30 con freq. 5,
e con (X-1000)/10 la distribuzione:
    -2 con freq. 3, -1 con freq. 5, 1 con freq. 7, 3 con freq. 5.

Per calcolare M(X) posso ricondurmi al calcolo della media di questa nuova distribuzione, ossia al calcolo di M((X-1000)/10):
  (-2·3-1·5+1·7+3·5)/(3+5+7+5) = (-6-5+7+15)/20 = 11/20
e poi fare:   11/20 · 10 + 1000 = 5.5 + 1000 = 1005.5.
    Infatti  M(X+k) = M(X)+k:  se sostituisco ogni dato x con x+k anche la media viene variata di k (l'istogramma si sposta orizzontalmente di k, con il suo baricentro - clicca l'immagine per ingrandirla).

E  M(kX) = M(X)·k:  se sostituisco ogni dato x con kx anche la media si moltiplica per k (ad es., se dilato l'istogramma raddoppiando le ascisse – e dimezzando le ordinate: l'area deve rimanere = 100% = 1 – anche l'ascissa del baricentro raddoppia - clicca l'immagine per ingrandirla).

    Nel caso del nostro esempio abbiamo usato prima M(X+k) = M(X)+k con k = -1000, poi M(X·k) = M(X)·k con k = 1/10.
    Queste proprietà sono comode nel calcolo a mano o mentale, ma anche impiegando una calcolatrice, in modo da diminuire il numero di tasti da battere, risparmiando tempo e riducendo la probabilità di commettere errori di battitura.
Se si usa R queste "comodità" (semplici ed utili da imparare per fare calcoli e stime a mente) si possono evitare con:
dati <- c(rep(980,times=3),rep(990,times=5),rep(1010,times=7),rep(1030,times=5))
mean(dati)
si ottiene 1005.5.

  Non valgono proprietà analoghe se i dati vengono trasformati mediante una radice quadrata o un elevamento al quadrato o ad un'altra potenza diversa da 1. Consideriamo ad esempio X e X², ossia la distribuzione avente come valori quelli di X elevati alla 2, con le stesse frequenze. Ad esempio, dato un insieme di quadrati di vari formati, X potrebbe essere la distribuzione delle lunghezze dei loro lati e X² quella delle loro aree. Sotto è raffigurato un possibile istogramma di distribuzione di X, in un caso in cui media e mediana di X siano 4, e quello di X².

La mediana dei dati elevati al quadrato è 16, il quadrato della mediana dei dati originali. Infatti elevando al quadrato i dati mantengono lo stesso ordine (x x² è una funzione crescente).
    La media invece è maggiore del quadrato della media; è 17. Infatti elevando al quadrato l'ordine di grandezza dei numeri lontani da 1 si modifica maggiormente di quelli vicini a 1; ciò dà luogo a una "coda" a destra nell'istogramma di X², che provoca lo spostamento a destra del baricentro.
•  Per un esempio semplice si pensi a 3 quadrati, uno di lato 1, uno di lato 2, l'altro di lato 3. La media dei lati è 2. Le loro aree sono invece 1, 4 e 9 e hanno come media 14/3 = 4.666…, che è maggiore di 2². Se consideriamo tre cubi di questi stessi lati, essi hanno volume 1, 8 e 27, con media 36/3 = 12, che è maggiore di 2³ = 8.
Questo fenomeno è collegato allla problematica dei fattori di scala [ diagrammi]: se trasformo delle grandezze mediante un elevamento a potenza diversa da 1 esse non mantengono le stesse proporzioni tra loro (a lato doppio non corrisponde area doppia o volume doppio).

 Se X è una distribuzione la sua varianza può essere descritta con Var(X) = M( (X – M(X))²):  è la media di ( X–μ )² dove μ = M(X), ossia è la media della distribuzione dei quadrati degli scarti dei dati di X dalla media di X.

    È ovvio che  Var(X+k) = Var(X):  gli scarti dalla media non variano se tutti i dati vengono aumentati o diminuiti di una stessa quantità in quanto la media, come abbiamo visto, varia della stessa quantità. In altre parole, la varianza non dipende dalla "posizione" dell'istogramma ma dalla sua forma, che non cambia se lo traslo orizzontalmente.

    Abbiamo poi  Var(kX) = k²Var(X)  e  σ(kX) (= √Var(kX) ) = kσ(X) (se k ≥ 0):  se moltiplico i dati per k anche gli scarti vengono moltiplicati per k, e quindi i loro quadrati, e la media di questi, vengono moltiplicati per k²; facendo la radice ottengo un valore moltiplicato per k rispetto a quello calcolato sui dati originali.

    Ad esempio nel caso dell'esempio X già considerato per M:
   980 con frequenza 3, 990 con freq. 5, 1010 con freq. 7, 1030 con freq. 5,
determinata (X-1000)/10:
    -2 con freq. 3, -1 con freq. 5, 1 con freq. 7, 3 con freq. 5
e M((X-1000)/10) = 0.55, con la calcolatrice (usando ) posso calcolare:
3(0.55+2)²+5(0.55+1)²+7(0.55-1)²+5(0.55-3)²
dividere per 20, fare la radice quadrata e ottenere:
σ((X-1000)/10) = 1.7741195
moltiplico per 10, arrotondo e ottengo:
σ(X-1000) = σ(X) = 17.7.
Con R posso semplicemente fare:
dati <- c(rep(980,times=3),rep(990,times=5),rep(1010,times=7),rep(1030,times=5))
sqrt(mean((dati-mean(dati))^2))
ottenendo: 17.74119

Spesso , ad esempio se si vogliono confrontare dati analoghi ma espressi con unità di misura diverse, può essere comodo ricorre all'indice di dispersione dato da σ(X)/M(X), noto come coefficiente di variazione e indicato CV(X), se X è la distribuzione statistica considerata. Infatti se moltiplico tutti i dati per k > 0, mentre il loro s.q.m. si modifica (abbiamo visto che viene moltiplicato per k), questo valore rimane uguale (in quanto anche la media viene moltiplicata per k). Lo si usa, ovviamente, se M(X) ≠ 0.

Un altro indice a volte usato è il coefficiente di asimmetria (skewness, in inglese), pari a M(((X–M(X))³)/σ³: è la media dello scarto cubico (dalla media), divisa per il cubo dello s.q.m. (in modo da "astrarre" dalla dispersione dei dati). Se i dati sono simmetrici rispetto alla media l'indice è nullo; se hanno una coda verso destra è positivo; se l'hanno verso sinistra, l'indice è negativo. Può andare da −∞ a ∞. Accanto a questo coefficiente di asimmetria ne sono impiegati altri, su cui non ci soffermiamo.

  Osserviamo che, se la nostra calcolatrice ha una sola memoria, e la usiamo per accumulare le somme dei quadrati degli scarti, dobbiamo battere tante volte la media (0.55 nell'esempio precedente) quanti sono i valori (se ha i tasti di parentesi possiamo mettere 0.55 in memoria e battere l'espressione per esteso). Vediamo se troviamo il modo di evitare ciò e, comunque, di battere meno tasti; partiamo ad es. dal caso in cui i dati siano 3:
Il calcolo della varianza è del tipo:
    ( (a – μ)² + (b – μ)² + (c – μ)² ) /3
che posso sviluppare in:
    ( (a²-2aμ+μ²) + (b²-2bμ+μ²) + (c²-2cμ+μ²) ) / 3
che posso riordinare in:
    ( (a²+b²+c²) - (2aμ+2bμ+2cμ) + (μ²+μ²+μ²) ) / 3
che raccogliendo posso trasformare in:
    ( (a²+b²+c²) - 2μ(a+b+c) + 3μ² ) / 3
che, considerando il fatto che (a+b+c)/3 = μ, posso riscrivere:
    ( (a²+b²+c²) - 2μ·3μ + 3μ² ) / 3
ossia:
    (a²+b²+c²)/3 – μ²
In generale, in modo analogo, otterrei  Var(X) = Σ_i x_i²/N – M(X)², ossia:
    Var(X) = M(X²) – M(X)².
Tornando al nostro esempio, dopo avere determinato (X-1000)/10:
    -2 con freq. 3, -1 con freq. 5, 1 con freq. 7, 3 con freq. 5
posso calcolare facilmente a mano o con la calcolatrice prima:
M((X-1000)/10) = 11/20 = 0.55,   e poi:
M(((X-1000)/10)²) = ((-2)²·3+(-1)²·5+1²·7+3²·5)/20 = (12+5+7+45)/20 = 69/20.
Infine   Var((X-1000)/10) = 69/20 - (11/20)² = (69·20-121)/20² = 1259/20²,
σ((X-1000)/10) = √1259/20,
σ(X-1000) = σ(X) = √1259 /20·10 = √1259/2 = 17.7.

Vedi qui se vuoi vedere come usare R - caricato source("http://macosa.dima.unige.it/r.R") - per affrontare l'argomento.

Esercizi:

 altri collegamenti     [nuova pagina]