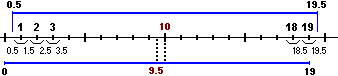Percentili
 Il concetto di percentile - o quantile - generalizza quello di mediana [ Il concetto di percentile - o quantile - generalizza quello di mediana [ valori medi 2]: valori medi 2]:
– la mediana è il dato che delimita il primo 50% dei dati (ordinati) dai rimanenti dati,
– se p è un numero tra 0 e 100, il percentile di ordine p (o p° percentile, se p è intero) è il dato che delimita il primo p% dei dati (ordinati) dai rimanenti dati.
(è usato anche il concetto di quartile: il 1º quartile è il dato che delimita il
primo quarto dei dati dai rimanenti, il 2º è quello che ne delimita i primi due quarti,
e coincide con la mediana, e il 3º è quello che ne delimita i primi tre quarti)
| 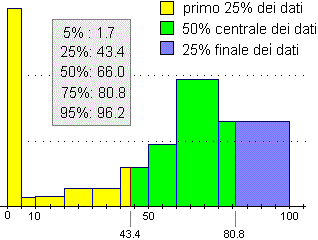 |
Nel caso del fenomeno considerato alle voci  distribuzione e
distribuzione e  valori medi 2, a cui si riferiscono l'istogramma soprastante e la seguente tabella delle frequenze cumulate, possiamo concludere che il 25° percentile cade tra 40 e 50 anni e che il 75° percentile cade tra 75 e 100 anni.
valori medi 2, a cui si riferiscono l'istogramma soprastante e la seguente tabella delle frequenze cumulate, possiamo concludere che il 25° percentile cade tra 40 e 50 anni e che il 75° percentile cade tra 75 e 100 anni.
| età dei morti (Italia,1951) | | freq. cumulata (in migliaia) | | freq. cumulata relativa |
|
| <5 |
<10 |
<20 |
<30 |
<40 |
<50 |
<60 |
<75 |
totale |
| 729 |
764 |
841 |
973 |
1107 |
1392 |
1849 |
3250 |
4819 |
| 15.1% |
15.8% |
17.4% |
20.1% |
22.9% |
28.8% |
38.3% |
67.4% |
100% |
|
Per stimare meglio questi percentili possiamo procedere in modo analogo a come è stato descritto per la
mediana [ valori medi 2] e trovare che
il 25° percentile e il 75° sono circa 43 anni e 80 anni.
valori medi 2] e trovare che
il 25° percentile e il 75° sono circa 43 anni e 80 anni.
 Se conveniamo di considerare normale l'intervallo costituito dal 50% centrale dei dati, cioè l'intervallo che va dal 25° al 75° percentile, possiamo dire che nel 1951 l'età di morte "normale" era compresa tra 43 e 80 anni. Si tratta comunque di una definizione convenzionale (potremmo prendere come intervallo di normalità quello che va dal 10° al 90° percentile o …), che può essere utile in molti casi, ma di cui occorre tener presente la natura puramente statistica; nel linguaggio comune l'aggettivo "normale" spesso assume connotati diversi.
Se conveniamo di considerare normale l'intervallo costituito dal 50% centrale dei dati, cioè l'intervallo che va dal 25° al 75° percentile, possiamo dire che nel 1951 l'età di morte "normale" era compresa tra 43 e 80 anni. Si tratta comunque di una definizione convenzionale (potremmo prendere come intervallo di normalità quello che va dal 10° al 90° percentile o …), che può essere utile in molti casi, ma di cui occorre tener presente la natura puramente statistica; nel linguaggio comune l'aggettivo "normale" spesso assume connotati diversi.
Ad esempio in un paese sottosviluppato il 50% centrale delle età di morte è molto più a sinistra, per es. può andare da 8 anni a 50 anni; ciò non vuol dire che sia "normale", nel senso di "accettabile", che una persona muoia in questa fascia di età. Il confronto con il corrispondente intervallo dell'Italia ci fa comunque capire che in quel paese vi sono delle condizioni di vita che non possono essere ritenute "normali" per un essere umano. Il confronto dei dati italiani del 1951 con quelli del 1988, in cui il 25° e il 75° percentile delle età di morte erano 64 anni e 88 anni, ci fa capire anche come, nella seconda metà del XX secolo, siano cambiate le condizioni di vita, le conoscenze e le tecnologie sanitarie, ... negli stessi paesi sviluppati.
Considerazioni analoghe si possono svolgere anche per il concetto di media.
 Nella figura a lato sono evidenziati i percentili di ordine 5, 25, 50, 75 e 95 (stimati fino ai decimi) della distribuzione dell'età di laurea presso l'Università di Genova nel triennio 1984-86. Nella figura a lato sono evidenziati i percentili di ordine 5, 25, 50, 75 e 95 (stimati fino ai decimi) della distribuzione dell'età di laurea presso l'Università di Genova nel triennio 1984-86.
I dati cadono in [22,41) (da 22 anni a 40 anni e rotti), la mediana (50° percentile) è 27.5, il 50% centrale dei dati cade tra 26.2 (25° percentile) e 29.2 (75° percentile).
Sotto all'istogramma è raffigurata una rappresentazione grafica alternativa, chiamata box-and-whiskers-plot ("diagramma a scatola e baffi") o, più in breve, box-plot.
È una figura "lineare" (si sviluppa solo orizzontalmente, non in due dimensioni, come gli istogrammi) che sintetizza in modo efficace come si distribuiscono i dati. | 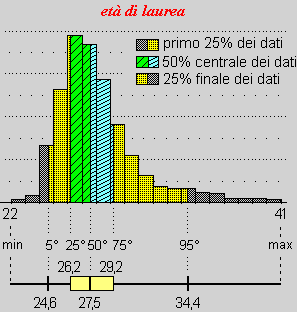 |
Il box (scatola) rappresenta il 50% centrale dei dati, le tacche lungo i baffi rappresentano il 5° e il 95° percentile, la tacca dentro al box rappresenta la mediana.
Il fatto che il box sia spostato verso sinistra (cioè che il baffo sinistro sia molto più corto di quello destro) corrisponde all'allungamento verso destra dell'istogramma.
I baffi avrebbero potuto essere tracciati anche riferendosi a percentili di ordine diverso
(ad es. con tacche per il 3° e il 97° invece che per il 5° e il 95°), o, come spesso di fa, escludendo i dati che distano dalla scatola più
di una volta e mezza della sua ampiezza.
 Per calcolare i percentili quando si ha una sequenza di dati (non dati classificati in intervalli come quelli considerati all'inizio della voce), ad es. nel caso dei
Per calcolare i percentili quando si ha una sequenza di dati (non dati classificati in intervalli come quelli considerati all'inizio della voce), ad es. nel caso dei  19 dati sulle altezze considerati per illustrare il concetto di mediana, si può procedere nel modo che ora descriviamo relativamente al 50° e al 25° percentile, e che poi generalizziamo:
19 dati sulle altezze considerati per illustrare il concetto di mediana, si può procedere nel modo che ora descriviamo relativamente al 50° e al 25° percentile, e che poi generalizziamo:
– il 50° percentile corrisponde al posto che separa il primo 50% dei dati, ma non posso semplicemente prendere il 50% di 19: 50/100·19 = 9.5; infatti il posto centrale è il posto numero 10; come si vede nella figura sottostante 9.5 corrisponde al centro dell'intervallo [0, 19], mentre dovrei considerare l'intervallo [0.5, 19.5], che come centro ha proprio 10;
– per trovare il posto che corrisponde al 50° percentile devo quindi prendere il centro di [0.5, 19.5] oppure prendere il centro di [0, 19], ossia 19/2, e aggiungere 0.5;
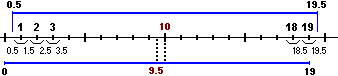
– analogamente il 25° percentile corrisponde al punto che dividide il primo 25% dell'intervallo [0.5, 19.5] dalla parte rimanente, ovvero il punto che si ottiene spostando a destra di 0.5 quello che dividide il primo 25% dell'intervallo [0, 19]: 25/100·19+0.5 = 4.75+0.5 = 5.25; 5.25 sta tra 5 e 6; usando la stessa convenzione adotatta per la mediana, tra i due posti scegliamo il primo: il 25° percentile è il 5° dato in ordine crescente, ossia 157;
– in generale per trovare il p-esimo percentile prendo il dato che (in ordine crescente) sta al posto ottenuto trocando agli interi p / 100 · NumeroDati + 0.5.
• Puoi provare a rivedere alcuni esempi
o affrontare alcuni degli esercizi proposti usando il programma R;
vedi qui per come costruire box-plot.
Esercizi: 
 altri collegamenti [nuova pagina]
altri collegamenti [nuova pagina]

 Il concetto di percentile - o quantile - generalizza quello di mediana
Il concetto di percentile - o quantile - generalizza quello di mediana  valori medi 2]:
valori medi 2]: