 Volendo scegliere l'ordine con cui passare
per 4 diverse località, ad es. nel caso in cui per lavoro, partendo da Genova, debba effettuare delle consegne a Milano, Torino, Piacenza e La Spezia, e poi tornare a Genova, ho:
Volendo scegliere l'ordine con cui passare
per 4 diverse località, ad es. nel caso in cui per lavoro, partendo da Genova, debba effettuare delle consegne a Milano, Torino, Piacenza e La Spezia, e poi tornare a Genova, ho:
Calcolo combinatorio
 Volendo scegliere l'ordine con cui passare
per 4 diverse località, ad es. nel caso in cui per lavoro, partendo da Genova, debba effettuare delle consegne a Milano, Torino, Piacenza e La Spezia, e poi tornare a Genova, ho:
Volendo scegliere l'ordine con cui passare
per 4 diverse località, ad es. nel caso in cui per lavoro, partendo da Genova, debba effettuare delle consegne a Milano, Torino, Piacenza e La Spezia, e poi tornare a Genova, ho:
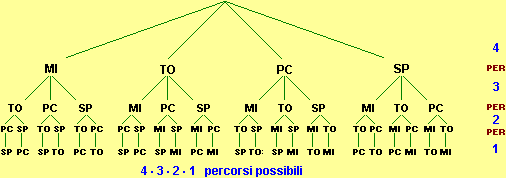
• 4
possibilità per la località "1" (cioè
per la prima località per cui passare);
• qualunque
sia stata la prima scelta ho poi 3 possibilità per la
località "2", e, quindi, le prime due località
posso sceglierle in 4·3 modi;
• qualunque
siano state le precedenti scelte ho poi 2 possibilità per la
località "3", e, quindi, le prime tre località
posso sceglierle in 4·3·2 modi;
• alla
fine la quarta scelta è obbligata, cioè ho 1 sola
possibilità, e, quindi, le 4 località posso
raggiungerle in 4·3·2·1 (= 24) percorsi diversi.
| Se le località per cui passare fossero state 6 i percorsi possibili sarebbero stati 6·5·4·3·2·1 (= 720) |
|
|||||||||||||||||||||||
| Analogamente posso disporre 5 commensali attorno a un tavolo in 5·4·3·2·1 (= 120) modi, le classifiche possibili tra 8 concorrenti sono 8·7·6·5·4·3·2·1 (= 40 320), … . | ||||||||||||||||||||||||
La funzione che a n, numero
naturale, associa la quantità
Quindi: 1! = 1, 2! = 2·1 = 2, 3! =
3·2·1 = 6, 4! = 4·3·2·1 = 24
Poiché nel caso di un insieme
costituito da 0 oggetti, cioè nel caso dell'insieme vuoto,
l'unica sequenza realizzabile è la sequenza vuota, pongo anche
0! = 1.
La funzione fattoriale può essere
definita  ricorsivamente così:
ricorsivamente così:
0! = 1, (n+1)!
= n!·(n+1).
I modi in cui posso ordinare n oggetti, cioè le sequenze di lunghezza n che posso realizzare con n oggetti, vengono spesso chiamati anche permutazioni di n oggetti (il nome deriva dal fatto che nel linguaggio comune "permutare" è sinonimo di "riordinare"). Quindi le permutazioni di n oggetti sono n! Viene usato anche il termine trasposizione per indicare una permutazione in cui viene scambiato tra loro il posto di due soli oggetti.
Nota. Se tra gli n oggetti ve ne sono r uguali non ci
importa in quale degli r! modi possibili questi sono ordinati (ordinato in un certo modo gli n
oggetti, abbiamo r! possibilità di riordinare gli oggetti uguali). Quindi in tal caso gli
effettivi ordinamenti sono
Esercizio: testo soluzione
Tale prodotto viene in genere indicato con
Dn,k o
con D(n,k).
Viene usata la lettera "D" in quanto le sequenze di lunghezza k
realizzabili con n oggetti vengono chiamate anche disposizioni
di n oggetti k a k: ogni sequenza è
interpretabile come uno dei modi in cui posso "disporre" k
oggetti scelti tra n. Tenendo conto che c'è solo la sequenza vuota costituita da 0 elementi,
si pone
 In un torneo a 11 di un particolare sport le prime 3 squadre classificate passano l'anno dopo al torneo regionale. Le possibili terne
In un torneo a 11 di un particolare sport le prime 3 squadre classificate passano l'anno dopo al torneo regionale. Le possibili terne  11·10·9. Per calcolare quanti sono i possibili terzetti di squadre che vengono "promosse" al livello superiore non ci interessa
la graduatoria tra le prime 3 squadre: al variare di questa (che può venire fuori in
11·10·9. Per calcolare quanti sono i possibili terzetti di squadre che vengono "promosse" al livello superiore non ci interessa
la graduatoria tra le prime 3 squadre: al variare di questa (che può venire fuori in  3·2·1 modi diversi) le
squadre che passano sono le stesse.
3·2·1 modi diversi) le
squadre che passano sono le stesse.
In altre parole tra le possibili terne (1a, 2a, 3a) ogni terzetto di squadre è
conteggiato 3! volte. Quindi il numero dei terzetti è:
n° totale delle terne 11·10·9 ————————————————————————————————————— = ——————— = 11·5·3 = 165 n° terne costituibili con un terzetto 3·2·1 |
Più in generale il numero dei sottoinsiemi di k elementi di un insieme di n elementi è pari al numero delle sequenze di k elementi che posso formare diviso per il numero dei modi in cui posso ordinare queste sequenze, cioè:
n° sequenze di k elementi n·(n-1)·…·(n-k+1) ——————————————————————————————— = ————————————————— n° permutazioni di una sequenza k·(k-1)·…·1 |
n n-1 n-k+1
= —·———·…·—————
k k-1 1 |
| [il rapporto tra il prodotto dei primi k numeri interi positivi a scalare da n e il prodotto di quelli a scalare da k] |
| I sottoinsiemi di k elementi di un insieme di n elementi vengono chiamati anche combinazioni di n elementi k a k. | |||||
|
|
 Quanti sono gli insiemi di 10 carte che si possono fare con le 13 carte di picche? (cioè, a ramino, quanti sono i modi di fare colore di picche?)
Quanti sono gli insiemi di 10 carte che si possono fare con le 13 carte di picche? (cioè, a ramino, quanti sono i modi di fare colore di picche?)
È il numero degli insiemi di 10 elementi che si possono fare con 13 elementi, cioè C(13,10). Allora dovrei calcolare:
13/10·12/9·11/8·10/7·9/6·8/5·7/4·6/3·5/2·4/1;
posso fare un po' di semplificazioni: "/10" e "·10" si annullano, e così "/9" e "·9", "/8" e "·8", …, "/4" e "·4", per cui alla fine rimane:
13·12·11/3/2/1 (=13·2·11 = 286), che equivale a C(13,3).
La cosa non deve stupire: scegliere 10 carte tra 13 equivale a sceglierne 3 da scartare:
 Voglio sviluppare (2+x)25. Come faccio a procedere senza fare per esteso tutte e 24 le moltiplicazioni (2+x)(2+x)…(2+x)? Abbiamo già visto in
Voglio sviluppare (2+x)25. Come faccio a procedere senza fare per esteso tutte e 24 le moltiplicazioni (2+x)(2+x)…(2+x)? Abbiamo già visto in  termini equivalenti
come velocizzare lo sviluppo di (A+B)n per n=2, ora vedremo un procedimento più generale.
termini equivalenti
come velocizzare lo sviluppo di (A+B)n per n=2, ora vedremo un procedimento più generale.
Il risultato delle 24 moltiplicazioni di cui sopra è la somma di:
2·2·…·2·2, 2·2·…·2·x, 2·2·…·x·2, 2·2·…·x·x, …, x·x·…·x·x,
cioè di tutti i prodotti ottenuti prendendo in tutte le 25 parentesi di (2+x)(2+x)…(2+x) o 2 o x. Dopo aver raggruppato i termini il risultato sarà un polinomio in x di grado 25.
Quale sarà il termine, ad es., di grado 22? x22 può essere ottenuto prendendo 22 volte x tra le 25 parentesi di (2+x)(2+x)…(2+x), e prendendo le altre 3 volte 2; i modi in cui si può far questo sono C(25,22), ovvero C(25,3), ossia 25·24·23/3/2 = 25·4·23 = 230; il termine di grado 3 è quindi 230·x22·23.
Più in generale il termine in A di grado k di (A+B)n sarà C(n,k)AkBn-k.
Per questo motivo  C(n,0), C(n,1), …, C(n,n) vengono chiamati anche coefficienti binomiali: sono i coefficienti dei termini A0Bn [=Bn], A1Bn-1, A2Bn-2, …, AnB0 [=An] del risultato della potenza n-esima del binomio A+B.
C(n,0), C(n,1), …, C(n,n) vengono chiamati anche coefficienti binomiali: sono i coefficienti dei termini A0Bn [=Bn], A1Bn-1, A2Bn-2, …, AnB0 [=An] del risultato della potenza n-esima del binomio A+B.
a+b = a + b
(a+b)^2 = a^2 + 2 a b + b^2
(a+b)^3 = a^3 + 3 a^2 b + 3 a b^2 + b^3
(a+b)^4 = a^4 + 4 a^3 b + 6 a^2 b^2 + 4 a b^3 + b^4
(a+b)^5 = a^5 + 5 a^4 b + 10 a^3 b^2 + 10 a^2 b^3 + 5 a b^4 + b^5
(a+b)^6 = a^6 + 6 a^5 b + 15 a^4 b^2 + 20 a^3 b^3 + 15 a^2 b^4 + 6 a b^5 + b^6
1 1 n=1
1 2 1 n=2
1 3 3 1 n=3
1 4 6 4 1 n=4
1 5 10 10 5 1 n=5
1 6 15 20 15 6 1 n=6
k = 0 1 2 3 4 5 6
|
Si può dimostrare che questo schema triangolare (noto come triangolo di Tartaglia o di Pascal o, meglio, triangolo artimetico, in quanto già noto almeno quattro secoli prima di Tartaglia), ottenuto disponendo sui lati sinistro e destro degli "1" e sommando man mano due a due gli elementi di una riga per ottenere gli elementi interni della riga successiva, fornisce effettivamente un metodo alternativo per calcolare C(n,k) per qualunque valore di n e k.
 Ho 6 oggetti, chiamiamoli A, B, C, D, E e F.
Voglio fare una confezione contenente alcuni di questi oggetti. In quanti modi posso farla?
Potrei fare una confezione vuota. Potrei fare una confezione contenente solamente A o solamente B o ….
Oppure una confezione contenente A e B o A e C o …. O potrei fare una confezione che li contiene tutti.
Quante sono le possibili confezioni? Una strategia per trovare quante sono è la seguente:
Ho 6 oggetti, chiamiamoli A, B, C, D, E e F.
Voglio fare una confezione contenente alcuni di questi oggetti. In quanti modi posso farla?
Potrei fare una confezione vuota. Potrei fare una confezione contenente solamente A o solamente B o ….
Oppure una confezione contenente A e B o A e C o …. O potrei fare una confezione che li contiene tutti.
Quante sono le possibili confezioni? Una strategia per trovare quante sono è la seguente:
per ognuno dei 6 elementi ho 2 possibilità: lo metto nella confezione o non ce lo metto:
• • • • • •
2 2 2 2 2 2 quindi in tutto ho 26 possibilità.
Più in generale i possibili sottoinsiemi di un insieme di n elementi sono 2n.
Potrei arrivare a questa conclusione anche in un altro modo:
• se a un insieme di N elementi aggiungo un nuovo elemento, il numero dei suoi sottoinsiemi raddoppia, infatti ai sottoinsiemi precedenti se ne affiancano altrettanti ottenuti aggiungendo ad essi il nuovo elemento;
• se indico con
• tenendo conto che un insieme di 0 elementi, ossia l'insieme vuoto, Ø, ha come unico sottoinsieme sé stesso, abbiano anche l'equazione:
• ma queste due equazioni non sono altro che la  definizione ricorsiva che equivale a porre
definizione ricorsiva che equivale a porre
L'insieme dei sottoinsiemi di un insieme A (che è eguale a 2^n se gli elementi di A sono n) viene chiamato insieme potenza di A.
 Quante sequenze costituite da 3 cifre decimali posso scrivere?
Ho 10 possibilità per la prima cifra, poi 10 per la seconda e, infine, 10 per la terza.
Le possibilità sono dunque 10·10·10 = 103 = 1000; del resto i numeri, da 000 a 999, sono 1000.
Quante sono le possibili coppie di uscite che si possono ottenere lanciando due dadi?
6 possibilità per il primo dado, 6 per il secondo; in tutto 6·6 = 62.
Quante sequenze di carte da un mazzo da 40 posso ottenere con 3 alzate? 40·40·40 = 403.
Quante sequenze costituite da 3 cifre decimali posso scrivere?
Ho 10 possibilità per la prima cifra, poi 10 per la seconda e, infine, 10 per la terza.
Le possibilità sono dunque 10·10·10 = 103 = 1000; del resto i numeri, da 000 a 999, sono 1000.
Quante sono le possibili coppie di uscite che si possono ottenere lanciando due dadi?
6 possibilità per il primo dado, 6 per il secondo; in tutto 6·6 = 62.
Quante sequenze di carte da un mazzo da 40 posso ottenere con 3 alzate? 40·40·40 = 403.
| • • • … • | Più in generale le possibili sequenze di k simboli tratti da un alfabeto di n elementi sono n·n·n·…·n = nk. | |
Queste sequenze vengono spesso chiamate anche disposizioni con ripetizione di n elementi k a k, in quanto, rispetto alle  disposizioni, ammettono la possibilità di utilizzare lo stesso elemento più volte nella stessa sequenza (in "999" il "9" compare tre volte). disposizioni, ammettono la possibilità di utilizzare lo stesso elemento più volte nella stessa sequenza (in "999" il "9" compare tre volte). | ||
 La branca della matematica che si occupa dei modi
in cui si possono formare nuovi oggetti (sequenze, insiemi, …) "combinando" gli elementi di un insieme finito viene chiamata
matematica combinatoria (o calcolo combinatorio).
La branca della matematica che si occupa dei modi
in cui si possono formare nuovi oggetti (sequenze, insiemi, …) "combinando" gli elementi di un insieme finito viene chiamata
matematica combinatoria (o calcolo combinatorio).
| Una caratteristica dei problemi di matematica combinatoria è che spesso si ha a che fare con situazioni in cui gli oggetti che vengono generati a partire da un insieme n di oggetti iniziali cresce rapidamente al crescere di n. A lato si vede come crescono rapidamente il numero dei diversi modi in cui si possono mettere in fila n oggetti e il numero dei diversi modi in cui si può formare un insieme prendendone gli elementi da un insieme di n oggetti. Di fronte a fenomeni di questo genere a volte si parla di esplosione combinatoria. Fenomeni di questo tipo sono anche all'origine di situazioni che intuitivamente sembrano altamente improbabili e che, invece, tali non sono. Ad es. non è affatto improbabile che una persona adulta attraverso 6 strette di mano abbia stabilito un contatto con il Presidente degli Stati Uniti: |
| ||||
| supponiamo che la persona abbia dato negli ultimi anni la mano
a solo 100 persone ciascuna delle quali a sua volta abbia dato la mano a 100 altre
persone, e così via; considerando complessivamente trascurabili le persone conteggiate più volte (possiamo farlo
in quanto, in realtà una persona ha dato la mano a ben più di 100 persone):
in tutto le persone raggiungibili con al più 6 strette di mano sarebbero
100·100·100·100·100·100 = 1006
= 1012 = mille miliardi, una quantità ben maggiore della popolazione mondiale. Questo calcolo ci può indurre a riflettere e a renderci conto che la cosa, in effetti, non è per niente strana: la persona può aver dato la mano al suo medico che, quando si è laureato, può aver dato la mano al preside della facoltà, che può aver dato la mano al rettore, che può aver dato la mano al ministro della pubblica istruzione, che può aver dato la mano al presidente della Repubblica Italiana, che può aver dato la mano a quello degli Stati Uniti. | |||||
 Come fare i calcoli
con R, ad esempio di 6!, D(8,3), Cbin(13,10):
Come fare i calcoli
con R, ad esempio di 6!, D(8,3), Cbin(13,10):
factorial(6); factorial(8)/factorial(8-3); choose(13,10)
720 336
286