Calcolo delle probabilità

  Nei giochi e nella "realtà" spesso si hanno da fare scelte di cui non si sanno prevedere esattamente le conseguenze (quale carta conviene scartare? in quale orario conviene partire per incontrare meno traffico in autostrada? …) o, comunque, si hanno da affrontare fenomeni di cui non si sa prevedere esattamente lo sviluppo (l'uscita di un dado, l'evolvere del tempo atmosferico, …).
    La parte della matematica che si occupa degli strumenti che permettono di razionalizzare le interpretazioni dei (e le scelte di fronte ai) fenomeni casuali (cioè di affrontarle ricorrendo alla ragione invece che affidandosi a pregiudizi, a superstizioni o al fato) è detta calcolo delle probabilità.
    Gli strumenti impiegati hanno una stretta parentela con quelli considerati nelle voci  "statistiche". Partiamo da tre semplici esempi.

Primo esempio.  Sta per disputarsi la partita Roma-Juventus. Gigi ritiene che la Roma 30 su 100 vincerà e 40 su 100 pareggerà. Qual è la probabilità per Gigi che vinca la Juventus?  Se da 100 tolgo 30 e 40 rimangono 30: per lui la Juve vince al 30 per 100. Volendo sintetizzare con qualche formula, uso Pr(…) per indicare la probabilità per Gigi che avvenga "…", indico con E l'esito della partita, che potrà essere "1", "2" o "X" (caratteri con cui indico rispettivamente la vittoria, la sconfitta o il pareggio della squadra di casa) ho:

Pr(E="1") = 30%,  Pr(E="X") = 40%,  Pr(E="1" OR E="X") = 30%+40% = 70%,  Pr(E="2") = 1 – Pr(E="1" OR E="X") = 1 – 70% = 30%.

| 1 | X | 2 | ||||||||||||||||||||||||||||||||||||||||||| | 3 0 % | 4 0 % | ? |

  Secondo esempio.  Voglio effettuare uno studio sociologico sui giovani e in questo ambito mi interessa valutare (1) la probabilità che un generico studente universitario si laurei compiuti i 29 anni e (2) quella che si laurei tra i 24 anni e mezzo e i 27 anni e mezzo. Considero l'istogramma, ovvero il box-plot, raffigurato alla voce percentili e ipotizzo (in assenza di altre informazioni) che anche ai nostri giorni e nei prossimi anni l'età di laurea si distribuisca in tal modo. Indico con E l'età di laurea e con  Pr(29 < E)  (o Pr(E>29)) e  Pr(24.5 ≤ E ≤ 27.5)  le due probabilità cercate.

(1)  Dal box-plot ricavo che il 75° percentile è 29.2, cioè circa 29 anni. Posso quindi stimare che la probabilità Pr(E≤29) di laurearsi al più a 29 anni sia 75%=0.75.    Da qui (vedi figura sotto a sinistra) posso ricavare la stima che Pr(29<E) = 100%–75% = 25% (se il 75% degli studenti ha E≤29 i rimanenti 25% hanno E>29).
[oltre che Pr(29<E)=25% posso dire anche che Pr(29≤E)=25% in quanto è trascurabile la probabilità Pr(E=29) che l'età di laurea sia esattamente 29 anni, cioè 29 anni e 0 giorni]
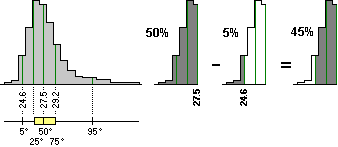(2)  Dal box-plot ricavo che 24.6 (che è circa 24.5, cioè 24 anni e mezzo) e 27.5 sono il 5° e il 50° percentile deducendone che Pr(E≤24.6)=5% e Pr(E≤27.5)=50%.     Gli studenti che si laureano tra 24.6 e 27.5 anni si ottengono sottraendo quelli che si laureano con meno di 24.6 anni da quelli che si laureano con meno di 27.5 anni (vedi figura sopra a destra); quindi: Pr(24.6≤E≤27.5) = Pr(E≤27.5)–Pr(E<24.6) = 50%–5% = 45%. Poiché 24.5 ≈ 24.6, posso concludere che Pr(24.5 ≤ E ≤ 27.5) ≈ 45%.
[ho considerato trascurabile la probabilità Pr(E=24.6), cioè ho identificato Pr(E<24.6) e Pr(E≤24.6)]

  Terzo esempio.  Voglio valutare la probabilità che lanciando un dado esca un numero pari. Suppongo che il dado sia equo, ovvero non sia truccato. Ciò significa supporre che l'uscita U abbia uguale probabilità di essere 1, 2, … o 6:
Pr(U=1) = Pr(U=2) = … = Pr(U=6).    Sia p il valore di questa probabilità.
Poiché  Pr(U=1)+Pr(U=2)+…+Pr(U=6) = 100% = 1, ho p+p+…+p = 6p = 1, da cui p=1/6.
Cioè:  Pr(U=1) = Pr(U=2) = … = Pr(U=6) = 1/6   Per trovare la probabilità che l'uscita sia pari posso fare:
Pr(U è pari) =Pr(U=2) + Pr(U=4) + Pr(U=6) = 1/6 + 1/6 + 1/6 = 3/6 = 1/2.

Posso rappresentare l'ipotesi che il dado sia equo con la figura a lato. Infatti l'ipotesi equivale a supporre che le uscite che si ottengono lanciando ripetutamente un dado tendano a distribuirsi secondo un istogramma in cui tutte le colonne abbiano la stessa altezza. La probabilità che un'uscita sia pari equivale alla somma delle frequenze delle colonne 2, 4 e 6, che corrispondono a metà della superficie dell'istogramma, ossia questa probabilità vale 50%.

Esercizi:   testo e soluzione,   testo e soluzione,   testo e soluzione

  Nel primo e nel secondo degli esempi precedenti ho associato ad alcuni eventi A un numero compreso tra 0 e 1 (=100%) come Pr(A) (probabilità di A).  Nel terzo ho fissato delle condizioni sulla funzione A → Pr(A): ho supposto che Pr(U=1) = Pr(U=2) = ….
    In tutti i casi ho poi dedotto le probabilità relative ad altri eventi applicando a Pr alcune delle proprietà che si erano già usate per le frequenze percentuali.
    Rivediamo più sistematicamente queste proprietà.

	• Pr(NOT A) = 100% – Pr(A) • Pr(A OR NOT A) = 100% =1 • Pr(A AND NOT A) = 0
Esempio:  Pr(E>29) = Pr(NOT E≤29) = 100% – Pr(E≤29)
	• Pr(A1 OR A2 OR A3 OR …) = Pr(A1) + Pr(A2) + Pr(A3) + … se  A1, A2, A3, … sono tra loro incompatibili, cioè se due qualunque eventi Ai e Aj non possono essere veri contemporaneamente.
Esempio:  Pr(U è pari) = Pr(U=2 OR U=4 OR U=6) = Pr(U=2)+Pr(U=4)+Pr(U=6)

   Quest'ultima proprietà è nota come proprietà additiva.

   La proprietà additiva vale nel caso di una sequenza A₁, A₂, A₃, … di eventi finita o infinita.  Ad esempio consideriamo una moneta truccata in cui testa esca con probabilità 0.9; lancio ripetutamente la moneta fino a che non esce "testa"; la probabilità che esca testa al primo lancio è 0.9 e quella che non esca è 0.1.  Anche al secondo lancio, che viene effettuato con probabilità 0.1, la probabilità che esca testa è 0.9.  Quindi la probabilità che esca testa nei primi due lanci è 0.9+0.1·0.9 = 0.9+0.09 = 0.99, e che non esca è 0.01.  In quest'ultimo caso effettuo un terzo lancio, e con probabilità 0.9 esce testa. Quindi la probabilità che esca testa nei primi tre lanci è 0.9+0.09+0.01·0.9 = 0.9+0.09+0.009 = 0.999.  Analogamente la probabilità che esca al quarto lancio è 0.9+0.09+0.009+0.0009 = 0.9999.  La probabilità che prima o poi esca testa è pari alla somma infinita 0.9+0.09+0.009+0.0009+0.00009+… = 0.999… = 1, ovviamente.

   Una proprietà analoga vale per le aree: se unisco dei poligoni l'area della figura risultante è la somma delle loro aree solo se essi non sono sovrapposti:

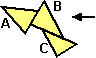Area(A U B U C) = Area(A) + Area(B) + Area(C) Area(A U B U C) ≠ Area(A) + Area(B) + Area(C)

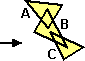   Vediamo una situazione in cui non si può applicare l'additività.  Conosco le percentuali degli studenti con insufficienze in matematica (42%), in fisica (39%) e in entrambe le materie (28%) del primo quadrimestre dell'anno passato nella scuola KK. Voglio valutare la probabilità che quest'anno uno studente debba essere coinvolto in corsi di recupero nell'area matematico-fisica, cioè valutare Pr(S∈ M OR S∈F) (ho indicato con S un generico studente, con M l'insieme di quelli insufficienti in matematica e con F quello degli insufficienti in fisica).
   Non posso usare la proprietà additiva e fare Pr(S∈M)+Pr(S∈F) poiché si può essere insufficienti in entrambe le materie, ma devo fare:
Pr(S∈M OR S∈F) = Pr(S∈M) + Pr(S∈F) – Pr(S∈M AND S∈F) = 42%+39%–28% = 53%
[il 28% degli insufficienti in entrambe è conteggiato due volte, devo dunque toglierne una]

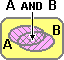Più in generale, di fronte a valutazioni del tipo Pr(A OR B) con A e B eventi non incompatibili, si usa la proprietà: •  Pr(A OR B) = Pr(A) + Pr(B) – Pr(A AND B)

    Questa proprietà come abbiamo visto, è una conseguenza delle altre evidenziate col pallino (•).  Anche la terza proprietà  (Pr(A AND NOT A) = 0)  è una conseguenza delle altre: prova a pensarci e arriverai facilmente a questa conclusione.

  Naturalmente, a seconda di come si scelgono le valutazioni iniziali, per la stessa situazione si possono ottenere diverse misure di probabilità. Le valutazioni iniziali possono essere dedotte dall'esperienza o da considerazioni di tipo fisico o da propri convincimenti o … . Devono comunque essere tali da non condurre a contraddizioni: a partire da esse, applicando ripetutamente le proprietà elencate nel punto precedente, non posso ottenere valutazioni diverse per uno stesso evento, non posso ottenere probabilità negative o superiori al 100%, … (ad es. non posso valutare 60% la probabilità che nella prossima partita Roma-Lazio vinca la Roma e 50% che pareggino; verrebbe contraddetta la prima proprietà).
Si osservi che il ruolo delle valutazioni iniziali mostra come anche in questo caso, come in altri discussi in altre voci, le conoscenze matematiche non sono di per sé sufficienti per modellizzare o risolvere "razionalmente" un problema. Per altri aspetti di come l'impiego di metodi matematici da solo non basti per affrontare scelte in condizioni di incertezza si vedano anche i seguenti esercizi:

testo e soluzione;   testo e soluzione.

La caratterizzazione del concetto di probabilità descritta sopra (non defininendo che cos'è la "probabilità" ma elencando le proprietà che deve avere una "misura di probabilità") è simile alla caratterizzazione di altri oggetti matematici (abbiamo visto ad esempio che vi sono diversi modi di definire una "distanza" tra due punti o, addirittura, diversi modi di definire uno "spazio"). Vedrai più avanti che le proprietà sopra elencate che deve avere una misura di probabilità per essere considerata tale vengono chiamate assiomi. Vedrai come anche lo spazio ed altri oggetti matematici possono essere definiti in questo modo: non esplicitando che cosa sono ma esplcitando le proprietà che essi devono soddisfare.

  Precisiamo meglio che cosa sono gli eventi.

   Chiamo fenomeno (o esperimento) casuale un fenomeno determinato da molti fattori alcuni dei quali li so valutare (so individuarli, ho gli strumenti per misurarli, non è troppo dispendioso rilevarli, … – nel caso del lancio del dado potrebbero essere le caratteristiche fisiche del dado), altri li ritengo casuali (nel caso del dado: l'impulso che gli dò, la rugosità e l'inclinazione della superficie della tavola, la presenza di correnti d'aria, …). La distinzione tra fattori casuali e non casuali è soggettiva, dipende dallo stato di conoscenze, dal tempo e dalle risorse che voglio dedicare all'analisi del problema, … : disponendo di strumenti sofisticati potrei misurare l'impulso che dò al dado, valutare la presenza di correnti d'aria, ….
    Chiamo condizioni l'insieme dei fattori che riesco a valutare. A parità di condizioni (ad es. usando sempre un dado della stessa forma, dello stesso materiale, …), un fenomeno casuale può realizzarsi diversamente; in altre parole, più prove dell'esperimento possono dar luogo a risultati diversi.
    Chiamo deterministico un fenomeno che non dipende da fattori casuali.
    Un evento è un fatto che riguarda un fenomeno casuale; ogni volta che, a parità di condizioni, il fenomeno si realizza, l'evento può verificarsi o no: nel contesto del lancio di un dado, un evento può essere, lanciato un dado, "esce la faccia del dado con 4 pallini"; nel contesto delle "insufficienze" un esempio di evento è, preso uno studente alla fine del 1° quadrimestre, "lo studente è insufficiente in matematica e non in fisica".
    Passando al modello matematico:

•  rappresentiamo il fenomeno individuando uno o più oggetti matematici che rappresentino le grandezze o gli aspetti attraverso cui si manifesta il fenomeno; li indichiamo con dei nomi, così come si fa per le variabili nelle formule che descrivono fenomeni deterministici; per questo essi sono chiamati variabili casuali;
•  gli eventi vengono rappresentati mediante formule (eventualmente combinate con operatori logici) in cui compaiono variabili casuali riferite al fenomeno in questione:
– nel caso del lancio di una coppia di dadi posso considerare i numeri U₁ e U₂ pari alle quantità dei pallini che compaiono sulle facce superiori dopo il lancio e rappresentare il fatto che "venga 7" con U₁+U₂=7
– nel caso delle insufficienze posso indicare con S lo studente e scrivere S∈M AND NOT S∈F per indicare l'evento "lo studente è insufficiente in matematica e non in fisica"

Esercizio   (soluzione)

Nota.  Le variabili casuali possono essere di tipo qualitativo o di tipo quantitativo. La distinzione non è però netta. Proviamo a precisarla.  Se consideriamo l'altezza delle persone di una certa popolazione, possiamo sicuramente considerarla come una variabile quantitativa: ad ogni altezza associamo un numero o, meglio, un intervallo di numeri reali (dire che una persona è altra 176 cm significa che la sua altezza in centimetri sta tra 175.5 e 176.5).  Se consideriamo il primo arrivato ad una corsa in cui i concorrenti sono individuati con dei numeri non possiamo considerarla una variabile quantitativa: i numeri sono semplicemente dei nomi usati per individuare i singoli concorrenti; possiamo considerarla una variabile qualitativa.  Questo semplice esempio pone però già qualche problema: se i numeri fossero assegnati ai concorrenti non a caso ma, ad esempio, tenendo conto della loro "bravura" (valutata ad esempio sulla base delle loro prestazioni dell'ultimo anno), potremmo individuare una qualche "relazione d'ordine".  Per un esempio più esplicito consideriamo i numeri 0, 1, 2, 3 usati per classificare il livello della attività sportiva fatta da degli individui intervistati, classificata attraverso degli opportuni criteri più o meno definiti. Non si tratta di una misura "fisica", però si tratta di dati che ha senso ordinare, e di cui, sotto opportune ipotesi, si possono anche trovare i valori medi. Questa è una variabile qualitativa o quantitativa? Considerazioni analoghe possono essere fatte, ad esempio, per i colori: in molti casi possono essere assunti come variabili qualitative, ma in altri possono essere considerati quantitative, quando, ad esempio, vengono impiegati per rappresentare altitudini, densità, frequenze, … diverse utilizzando la loro codifica numerica ( colori).  In definitiva, una distinzione netta non può essere fatta in assoluto: dipende dal tipo di analisi a cui si vogliono sottoporre i dati.  Nel caso degli esempi semplici considerati in questa scheda posso comunque dire che mentre E nel secondo è una variabile quantitativa nel primo è una variabile qualitativa.

  Se U è una variabile casuale a cui si è associato, come insieme di valori su cui può variare, un insieme di oggetti matematici {a₁,a₂,a₃,…}, dotare U di una legge di distribuzione vuol dire descrivere come calcolare i valori di una misura di probabilità Pr per gli eventi U = a_i.

•  Nel caso del lancio di un dado, indicata con U l'uscita, posso associare a U come insieme di valori possibili l'insieme finito {1,2,…,6} e, se ipotizzo che il dado sia equo, considerare la misura di probabilità Pr così definita per ogni h in {1,2,…,6}:  Pr(U=h) = 1/6. Posso rappresentare tale legge di distribuzione anche con l'istogramma visto sopra.
    In questo caso ho dotato U di una legge di distribuzione uniforme sull'insieme {1,2,…,6}.
    Per calcolare Pr(U è pari) invece di procedere come ho fatto in precedenza, posso osservare che l'esito di sommare 1/6 tante volte quanti sono i casi "favorevoli" (cioè 3 volte, quanti sono i numeri pari) è pari a 3/6.
    Analogamente, nel caso di U distribuita uniformemente su un insieme finito di n elementi, se so che un evento A equivale all'uscita di uno tra k elementi, si dice che i casi possibili sono n, i casi favorevoli sono k e Pr(A) può essere calcolata facendo k / n.
•  Supponiamo di lanciare ripetutamente una moneta fino a che non esce "testa" (T). Vogliamo valutare il numero N dei lanci necessari. In questo caso i valori che può assumere N non sono in quantità finita, come invece accadeva per U nell'esempio precedente: sarà N=1 se esce T al primo lancio, N=2 se esce T al secondo lancio, …. Non esiste un limite superiore al valore che può assumere N: la moneta potrebbe essere truccata in modo tale che non esca mai T, o, anche se essa fosse equa, potrebbe capitare che esca sempre "croce" (C) per una lunga sequenza di lanci, senza che a priori si possa stabilire quanto sia questa lunghezza.
    Proviamo a valutare Pr(N=2) nel caso in cui la moneta sia equa. Al primo lancio al 50% (cioè con probabilità 1/2) esce T, e mi fermo, e al 50% esce C, e proseguo; quindi Pr(N=1)=50%. Se effettuo un secondo lancio ho nuovamente che possono uscire con la stessa probabilità sia T (nel qual caso mi fermo: N=2) che C (nel qual caso proseguo: N>2). Quindi Pr(N=2) è la metà di 50%, cioè 25%.
    Analogamente l'evento N=3 equivale all'uscita di T al terzo lancio, ed ha probabilità metà di 25%, cioè 12.5% (1/8). Più k è grande; più Pr(N=k) è piccolo: ad ogni incremento di 1 di k Pr(N=k) si dimezza. Il fatto che siano necessari 5 lanci è poco probabile (Pr(N=5) = 1/2/2/2/2/2 = 3.125%), ma non impossibile.

  Se invece a U è associato, come insieme di valori su cui può variare, un intervallo I di numeri, dotare U di una legge di distribuzione vuol dire descrivere come calcolare i valori di una misura di probabilità Pr per gli eventi del tipo U∈J con J sottointervallo di I.

   Nel caso dell'esempio della età di laurea E, l'assunzione che E si distribuisca come nel box-plot raffigurato alla voce percentili è traducibile così:
Pr(E ≤ 24.6) = 5%,  Pr(E ≤ 26.2) = 25%,  Pr(E ≤ 27.5) = 50%,  Pr(E ≤ 29.2) = 75%,  Pr(E ≤ 34.4) = 95%.
    In questo caso, usando le proprietà di Pr sono in grado di valutare probabilità di vari eventi del tipo E∈J con J sottointervallo di [0,), anche se non di tutti:  so calcolare Pr(E∈(26.2, 34.4]) (= 95%–25% = 70%) ma non so calcolare Pr(E∈[28, 32)).
    Se invece avessi a disposizione le informazioni fornite dall'istogramma raffigurato sopra al box-plot, potrei valutare Pr(E∈J) per tutti gli intervalli J del tipo [m,n) con m e n interi. Ad esempio per Pr(E∈[28, 32)) potrei ricavare le probabilità che E cada in [28,29), [29,30), [30,31), [31,32) e sommarle, ottenendo 32%.

  Il generatore di numeri pseudocasuali (RND in QBasic, random() in JavaScript, runif(1) in R - runif(n) genera una n-upla di numeri pseudocasuali), è una "funzione a 0 argomenti" presente nei linguaggi di programmazione (e nei fogli di calcolo e in molto software matematico) che (ogni volta che è incontrata nel corso dell'esecuzione) assume un valore che cade in [0,1) con legge di distribuzione uniforme. In questo caso ciò significa che, presi comunque due sottointervalli J e K di [0,1) di uguale ampiezza, Pr(RND∈J) = Pr(RND∈K), dove con RND abbiamo indicato le uscite della funzione "generatore di numeri pseudocasuali". RND è usabile per simulare altre variabili casuali (ossia creare degli oggetti matematici che si comportino come esse).
    Ad es. in QBasic l'assegnazione U=FIX(RND*6)+1 (FIX è la funzione che tronca agli interi) dà alla variabile U una distribuzione uniforme in {1,2,…,6}, così da simulare, ad es., il lancio di un dado equo:

	*6		FIX		+1
[0, 1)	→	[0, 6)	→	{0,1,2,3,4,5}	→	{1,2,3,4,5,6}

    Invece U1=FIX(RND*6)+1: U2=FIX(RND*6)+1: U=U1+U2 dà luogo a una variabile U che simula il lancio di due dadi equi.
    U1 <- floor(runif(1,min=1,max=7)); U2 <- floor(runif(1,min=1,max=7)); U <- U1+U2 è ciò che avrei dovuto battere in R.
    Si chiamano "pseudocasuali" e non "casuali" in quanto la casualità è apparente: in realtà il funzionamento di RND è governato da un sottoprogramma incorporato nel programma traduttore (pseudo è un prefisso di origine greca che significa "falso", "fittizio", come in "pseudonimo" = "falso nome", "pseudoscientifico" = "presentato falsamente come scientifico").

Ad esempio per valutare la probabilità che lanciando due dadi si ottenga un'uscita maggiore di 7 possiamo impiegare il programma seguente (clicca QUI [o qui o qui] per una versione in R; qui per una versione in JavaScript; qui (o qui) invece trovi la generazione dell'istogramma di distribuzione all'aumentare dei lanci):
n = 0: ok = 0  Prova:   U1 = FIX(RND*6)+1: U2 = FIX(RND*6)+1   n = n+1: IF U1+U2 > 7 THEN ok = ok+1   PRINT n, ok/n*100;"%" GOTO Prova  che simula il lancio ripetuto di una coppia di dadi, il conteggio (mediante n) delle prove effettuate e (mediante ok) di quelle in cui l'uscita ha superato 7, e il calcolo della frequenza relativa delle uscite maggiori di 7. Si vede dagli output (a lato ne è riprodotta una possibile sequenza) che la frequenza tende a stabilizzarsi attorno a 42%. Possiamo assumere questa come probabilità del nostro evento. Nota. In questo caso era facile determinare la probabilità anche per via teorica:  le "possibili" coppie di uscite, tra loro equiprobabili se i dadi sono equi, sono 6·6 = 36  – (1,1), (1,2), …, (1,6), (2,1), …, (2,6), …, (6,6) –  mentre quelle "favorevoli", che danno luogo ad un numero maggiore di 7, sono 1+2+3+4+5 = 15  – (2,6), (3,5), (3,6), (4,4), (4,5), (4,6), …, (6,6) –  per cui () la probabilità è 15/36 = 5/12 = 0.41666….		n frequenza 1 0% 2 50% 3 33.33333% 4 25% 5 20% ... ... 10 50% ... ... 100 33% ... ... 1000 40.1% ... ... 10000 41.48% ... ... 100000 41.777% ... ... 1000000 41.6927% ... ... 2000000 41.7299% ... ...

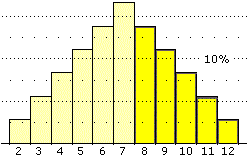
La tabella sottostante riporta le uscite di U1+U2 al variare di U1 e U2.  L'istogramma illustra la legge di distribuzione di U1+U2. L'uscita più probabile è 7, in quanto è quella formabile in più modi. Le parti in giallo scuro corrispondono all'evento U1+U2>7.  Nel caso dell'istogramma la parte scura è i 5/12, ossia il 41.7%, dell'intera superficie.
	U2=1 U2=2 U2=3 U2=4 U2=5 U2=6 U1=1  2 3 4 5 6 7 U1=2 3 4 5 6 7 8 U1=3 4 5 6 7 8 9 U1=4 5 6 7 8 9 10 U1=5 6 7 8 9 10 11 U1=6 7 8 9 10 11 12

  Spesso si tende ad affrontare ogni problema probabilistico cercando di calcolare un rapporto del tipo: "casi favorevoli" su "casi possibili", a cui, come abbiamo visto sopra, si può ricorrere nel caso di distribuzioni finite ed uniformi. Ma a volte lo si fa erroneamente.
    Ad esempio c'è chi può pensare che la probabilità di fare 4 lanciando due dadi sia 1/11, in quanto 4 è 1 tra le 11 uscite possibili (2, 3, …, 12). Facendo così non tiene conto che le 11 uscite non sono tutte equiprobabili.  O c'è chi può pensare che sia 2/36, in quanto 4 posso ottenerlo se escono due 2 o se escono un 1 e un 3 (2 casi favorevoli) mentre i possibili esiti di un lancio sono dati da 6 possibili uscite per il primo dado a ciascuna delle quali possono corrispondere 6 uscite diverse del secondo (6 per 6 casi possibili). Qui l'errore consiste nel non tener conto che l'uscita di un 1 e un 3 posso ottenerla in due modi: l'1 col primo dado e il 3 col secondo, o viceversa. I casi favorevoli sono dunque 3, non 2.
    In altre situazioni non si tiene conto che questo schema di calcolo funziona solo se la distribuzione è uniforme, come quando un insegnante decide di interrogare tra i suoi 18 alunni quello il cui numero d'ordine sul registro di classe è dato dalla somma delle cifre della pagina di un libro aperto a caso, supponiamo senza privilegiare alcuna parte del libro (una pagina verso l'inizio abbia la stessa probabilità di essere pescata di una centrale o una finale). L'insegnante pensa che ogni alunno abbia 1/18 come probabilità di essere chiamato.  Ma … se per es. il libro ha 100 pagine, il primo e il secondo alunno hanno probabilità 3/100 = 3% di essere sorteggiati (pagine 1, 10, 100 per il 1°, pagine 2, 11, 20 per il 2°), il 3° 4% (3, 12, 21, 30), … il 18° 1% (99). Il più sfortunato è l'alunno n. 9, con il 10% di probabilità di essere pescato.
    Vi sono, poi, volte in cui si accetta acriticamente che una distribuzione sia uniforme. Consideriamo ad esempio due dadi di carta realizzati utilizzando materiali e indicazioni presenti in un giornalino per bambini (vedi la figura seguente). Se ammettiamo che la distribuzione delle 6 uscite sia uniforme, possiamo concludere che lanciando due dadi si hanno le stesse probabilità di ottenere 2 (1+1) e 12 (6+6). È corretta questa ipotesi?

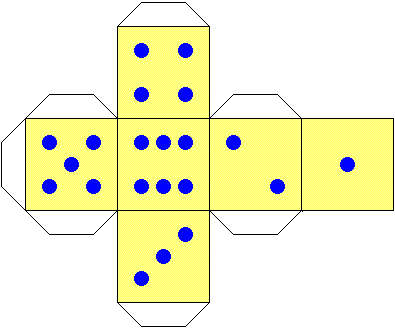
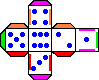
    Come si vede nella figura sopra a destra, mentre sulla faccia "1" sono incollate 3 linguette, sulla faccia "6" non ve ne sono: lanciando un dado è più facile che esca 6 in quanto la sua faccia opposta è più pesante. In effetti se si costruiscono i dadi si può verificare sperimentalmente che il 6 esce con frequenza più che doppia rispetto all'1, e che lanciando due dadi ottenere 12 è abbastanza frequente mentre ottenere 2 è molto raro. [animazioni e approfondimenti: ]

  Gli errori discussi sopra sono in parte causati da confusioni concettuali originate da insegnamenti o libri di testo in cui la probabilità viene definita con frasi del tipo: «si chiama probabilità di un evento il rapporto tra il numero dei casi favorevoli al verificarsi dell'evento e il numero dei casi possibili, purché questi siano ugualmente possibili», scambiando per una definizione quello che è un metodo di calcolo applicabile solo sotto ipotesi molto restrittive.
Per  diversi aspetti questo è un errore più grave dei precedenti. È un errore "didattico" poiché fonte dei fraintendimenti concettuali di cui abbiamo discusso (il "purché …" viene cancellato dalla memoria dagli esercizi ripetitivi in cui si fa poi applicare la definizione). È un errore "tecnico" perché contiene un "circolo vizioso": definisce la probabilità utilizzando il concetto stesso di probabilità: si dice che i casi devono essere "equiprobabili" (supponendo che sia questo che si vuole intendere con "egualmente possibili", perché, a rigore, l'aggettivo "possibile", a differenza dell'aggettivo "probabile", non dovrebbe essere quantificato). Ed è un errore "concettuale", in quanto cattura solo situazioni molto particolari (non si adatta, ad es., ai primi due esempi considerati in questa voce, che corrispondono a situazioni molto comuni in cui si fanno valutazioni probabilistiche).

  Un errore di tipo diverso è quello di basarsi sugli esiti sperimentali di un fenomeno che si ripete (come il lancio di un dado, le uscite al gioco del lotto, …) anche quando si conosce la legge di distribuzione del fenomeno stesso e si sa che ogni nuovo evento accade in modo del tutto indipendente dai precedenti (si usa un dado non truccato, le estrazioni del lotto sono effettuate senza imbrogli, …).  Ad es., riferendoci al gioco del lotto, se sulla ruota di Genova il 13 non esce da 50 estrazioni e il 17 non esce da 70, non c'è alcun motivo per ritenere che alla prossima estrazione sia più probabile l'uscita del 17 rispetto a quella del 13: entrambi hanno la stessa probabilità di uscita in quanto siamo di fronte a una distribuzione uniforme.  In una voce successiva è ulteriormente approfondito il concetto di  indipendenza tra due eventi.

Esercizi: (fino a 1.6)  

 altri collegamenti     [nuova pagina]