Rappresentazione decimale dei numeri

  Si chiama rappresentazione decimale dei numeri la loro usuale scrittura, che impiega le dieci cifre 0, 1, 2, …, 9 ed eventualmente un punto (o una virgola) e il segno "–" (simbolo di negazione, o simbolo "meno").

Il segno "–" distingue un numero dal suo opposto, ossia da quello che, rappresentando i numeri su una retta, sta in posizione speculare rispetto a 0: se considero passi lunghi due quadretti e indico con 4 la posizione che raggiungo allontanandomi dalla posizione "zero" di 4 passi a destra, -4 indica la posizione che raggiungo con la stessa quantità di passi andando in direzione opposta;  la "distanza" percorsa si chiama valore assoluto:  4 e -4 hanno lo stesso valore assoluto: 4.

Nel seguito ricordiamo il significato del segno "." (il punto decimale, che in Italia, nelle attività commerciali, spesso è sostituito con ",", la virgola decimale) e le diverse quantità che rappresentano le cifre a seconda della loro posizione.

A fianco è raffigurato, mentre sta passando da 9 a 10, un contagiri che rappresenta la quantità di giri in forma decimale. [ animazione]     Esso illustra bene il significato della scrittura decimale: ogni dieci aumenti di una unità si ha un aumento di una decina, ogni dieci aumenti di una decina si ha un aumento di un centinaio, ...   Il riquadro seguente generalizza questo esempio e ricorda che cos'è il posto di una cifra:

– se con un numero si vuole rappresentare una certa quantità di "cose", la cifra di posto 0 rappresenta quante volte (0,1,… o 9) deve essere presa una copia della cosa (nel caso dell'esempio iniziale le "cose" erano i "passi" di cui spostarsi); 
– andando verso sinistra, le cifre di posto maggiore indicano quante volte devono essere prese porzioni di cose man mano pari a 10 volte la porzione precedente (al posto 1 sono indicate quante decine, ossia porzioni costitituite da 10 cose, prendere; al posto 2 quante porzioni da 100 cose prendere; …) 
– andando a destra della cifra di posto 0, le cifre di posto minore indicano quante volte devono essere prese porzioni di cosa man mano pari a un decimo della porzione precedente; queste cifre, che rappresentano frazioni di "cosa", vengono dette cifre frazionarie.

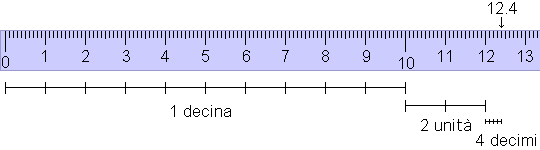
Nel caso di 12.4 cm (→ figura seguente) la "cosa" è 1 cm.

Quando la "cosa" è una unità di misura fondamentale di una grandezza fisica (grammo, secondo, metro, …) per indicare alcuni "multipli" e "sottomultipli" di essa si usa premettere al simbolo (g, s, m, …) che la rappresenta un opportuno prefisso; ad es. km, cm, mm e μm (micrométro o micron) stanno a indicare, in ordine, un migliaio di metri, un centesimo, un millesimo e un milionesimo di metro.  Quindi 12.4 cm, che sta per 12.4 centesimi si metro, equivale a 12.4/100 m = 0.124 m.

  Un numero privo di cifre frazionarie (o le cui cifre frazionarie sono tutte 0, come 13.000…) viene detto numero intero: esso indica che non occorre prendere frazioni (decimi, centesimi,…) della "cosa" di cui si vuole esprimere una quantità.

	Si dice che: 83628 ha ordine di grandezza delle decine di migliaia, 3.56 ha ordine di grandezza delle unità, 0.02419 dei centesimi, … .    Si può pure dire che 83628 ha ordine di grandezza 4, 3.56 ha ordine di grandezza 0, 0.02419 ha ordine di grandezza -2. In generale l'ordine di grandezza di un numero è il posto della sua prima cifra a sinistra diversa da 0.
Qualcuno dice anche che 83628 ha ordine di grandezza 100 mila o ha ordine di grandezza del centinaio di migliaia, intendendo che 100 mila è la potenza di 10 a cui 83628 è più vicino.
Nota.  Quest'ultimo modo di esprimersi presenta comunque qualche ambiguità: 540 è più vicino a 100 che a 1000 (infatti a metà tra questi valori c'è 550, non 500) ma verrebbe naturale pensare più all'ordine di grandezza del migliaio che all'ordine di grandezza cento. Chi usa la definizione citata probabilmente, confondendosi con i criteri che si usano per arrotondare [ Approssimazioni], crede, sbagliando, che essa sia equivalente alla seguente: un numero ha come ordine di grandezza la potenza di 10 che compare nella sua espressione in notazione scientifica se la sua prima cifra è minore di 5, la potenza di 10 di esponente successivo altrimenti.  Con questa definizione 540 avrebbe effettivamente 1000 come ordine di grandezza. Si tratterebbe, comunque, di una definizione poco significativa: pensando alle potenze di 10, poiché 10 alla 2.5 (numero a metà tra 2 e 3), ossia √100000 [per le potenze a esponente non intero potenze (2) ], fa 316.227... e 10 alla 3.5, ossia √1000000, fa 3162.27..., sarebbe forse più corretto dire che i numeri compresi tra 316.227... e 3162.27... hanno ordine di grandezza del migliaio.

Esempio: la velocità in km/h massima di una tartaruga ha ordine di grandezza –2 (cioè dei centesimi di km/h) quella di un'aquila 2 (centinaia di km/h). Quindi il rapporto tra la velocità di un'aquila e quella di una tartaruga è circa 10²/10^–2 = 10^2–(–2) = 10⁴: la velocità dell'aquila è circa 10 mila volte quella della tartaruga.

  Spesso i numeri che hanno ordine di grandezza negativo (cioè inferiore a quello delle unità), come 0.57, 0.024, ..., vengono scritti trascurando la cifra 0 prima del punto, cioè nella forma: .57, .024, … . Così si comportano durante la stampa o la visualizzazione delle uscite molti programmi per computer. Anche impiegando una calcolatrice si può evitare di battere lo 0 iniziale.

  Il punto (o la virgola) decimale nel linguaggio orale viene letto spesso "e"; ad esempio "1.23" viene letto "uno punto ventitre" o "uno e ventitre", oltre che "uno e ventitre centesimi"; di fronte a "5.03", se non si aggiunge "centesimi", occorre dire "cinque e zero tre", per evitare di confoderlo con "5.3". Ma è meglio usare "punto" o "virgola" al posto di "e" (a meno che non si aggiunga "centesimi" o "decimi" o … a seconda dei casi).  Nei dialoghi quotidiani spesso si usano convenzioni diverse a seconda del contesto in cui ci si trova. Ad esempio parlando di automobili, con "cilindrata mille e tre" non intendiamo 1003, ma 1300, ossia "mille e trecento"; in altre parole si sottintende il "cento". Parlando di soldi, con "un euro e tre" in genere si intende 1.03 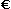, ossia "un euro e tre centesimi", non 1.3 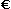(ossia "un euro e trenta centesimi").

Esercizio 1:  testo   e   soluzione Esercizio 2:  testo   e   soluzione Esercizio 3:  testo   e   soluzione     [esercizi più semplici: ]

L'UNO e lo ZERO

 altri collegamenti     [nuova pagina]