more
Da L'insegnamento della matematica e delle scienze integrate, vol. 18 B, n.2, 1995
L'INSEGNAMENTO DELLA GEOMETRIA NELLA
SCUOLA SECONDARIA SUPERIORE – 1a
parte
Arturo
Bosco, Carlo Dapueto, Maria Teresa Gaggero, Carlo Mortola, Gabriella Tiragallo
Nucleo di Ricerca Didattica MaCoSa
c/o Dipartimento di Matematica dell'Università di Genova
Summary
In the 1st part of this paper we present the questions we have put to the partecipants in a refrescher course (for secondary school teachers) on Geometry teaching. The questions have the aim of pointing out and clarifying some cultural and didactic aspects we think basic for planning curricula and activities on this subject.
In the 2nd part we discuss the questions and some problems related to them.
Introduzione
Nel
1993 il nucleo di ricerca didattica MaCoSa ha promosso un corso di aggiornamento sull'insegnamento della
geometria nella scuola secondaria superiore. La preparazione del
corso è stata curata dal gruppo di lavoro che si sta occupando
della progettazione delle unità didattiche riferite ai temi
geometrici.
Gli insegnanti
che intendevano partecipare al corso dovevano ritirare una settimana
prima dell'inizio di esso un fascicolo in cui erano proposti alcuni
quesiti su cui dovevano riflettere e la cui discussione è
poi stata impiegata come canovaccio per la conduzione del corso. In
questo articolo riportiamo il materiale impiegato per il corso, con
qualche taglio e alcune piccole modifiche. Per dare natura
"operativa" all'articolo, lo abbiamo spezzato in due
parti.
In questa 1a
parte riportiamo i quesiti. Nella 2a
parte, che verrà pubblicata successivamente, verranno
analizzate le questioni sollevate dai quesiti stessi.
I quesiti verranno utilizzati anche
come base per il gruppo di lavoro sull'insegnamento della geometria
che condurremo nell'ambito del 17° Convegno dell'U.M.I.
sull'insegnamento della matematica.
I quesiti proposti
|
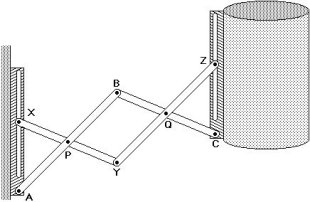
Q1 Considera
il dispositivo descritto in figura 1. Come
motiveresti a una persona che non abbia compiuto (o non ricordi)
studi di tipo geometrico il fatto che (se il sostegno a sinistra è
fissato verticalmente) il contenitore, comunque venga allontanato dal
sostegno, si mantiene in posizione verticale?
Q2 Come
modellizzeresti matematicamente la situazione e con quale
proposizione descriveresti quanto
sopra affermato? |
figura 1
 |
|
Q3 Prova
a esplicitare in tutti i passaggi come tale proposizione è
dimostrabile usando gli assiomi e le definizioni presenti in un libro
di testo recente che offra una presentazione completa della geometria
piana (ripercorri anche le dimostrazioni dei teoremi intermedi). Fai
la stessa cosa riferendoti ai libri seguenti, di cui nelle appendici
1 e 2 abbiamo riportato estratti con assiomi, definizioni
e teoremi rispettivi:
– F.Enriques-U.Amaldi, Elementi di Geometria (edizione ridotta), Bologna, 1936
– G.Prodi, Matematica come scoperta, Messina-Firenze, 1977
Confronta
le differenze tra i diversi itinerari dimostrativi e tra questi e il
modo in cui si può spiegare a una persona "normale"
il principio di funzionamento del dispositivo considerato.
|
Q4 In
vari libri di testo i criteri di eguaglianza per i triangoli vengono
introdotti nel modo seguente.
In capitoli o
paragrafi introduttivi sulla natura della geometria si spiega che
tutte le proposizioni devono essere dimostrate a partire dagli
assiomi e che tutti i concetti devono essere definiti a partire dai
concetti primitivi, il cui significato è caratterizzato
implicitamente dagli assiomi. Tra i concetti primitivi si pongono
quelli di punto, retta, piano e movimento rigido. Vengono
definite uguali due figure quando esiste un movimento che
porta una di esse a coincidere punto per punto con l'altra. Come
postulato relativo al movimento si pone solo quello che l'eguaglianza
così definita è una relazione di equivalenza.
Più avanti si trovano
dimostrazioni del 1° criterio di eguaglianza dei triangoli
sintetizzabili così:
Ipotesi:
AB=MN, AC=MP, ∠A=∠M.
Tesi:
ΔMNP=ΔABC
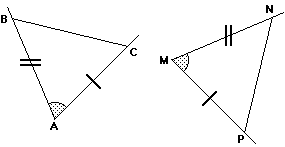
figura 2 |
Poiché
∠A=∠M,
esiste un movimento che fa sovrapporre le semirette MN e MP
rispettivamente alle semirette AB e AC.
Poiché
AB=MN e AC=MP lo stesso movimento deve far coincidere pure N con B
e P con C.
Quindi con
un movimento è possibile far coincidere i vertici dei due
triangoli, che sono dunque uguali.
 |
(1) Pierino, un po'
cocciuto e senza un grande feeling con l'insegnante di matematica,
che ha adottato un libro del tipo sopra descritto, non capisce a che
serve dimostrare l'eguaglianza di due figure che sono evidentemente
uguali.
(2) Poi, gli sembra
che qualcosa non torni nel ragionamento condotto dal libro, ma non
riesce a precisare meglio questa sensazione.
(3) Infine, quando
si trova a dover studiare il 3° criterio di eguaglianza, alla cui
dimostrazione il libro dedica quasi due facciate, perde ogni fiducia,
non sa se in sé o nella matematica: perché tanti
discorsi quando era facile procedere con qualche "movimento"
come nel caso del 1° criterio?
Discuti
(1), (2) e (3).
|
Q5 L'insegnante
propone agli alunni di dimostrare (per assurdo) che se (vedi
figura 3) le rette RS e PQ sono parallele,
due angoli interni che sono dalla
stessa parte rispetto alla trasversale HK hanno come somma 180°.
Gigi procede in questo modo:
Supponiamo che la somma degli angoli interni che stanno
dalla stessa parte rispetto alla trasversale sia maggiore di 180°.
Allora a+b>180°,
c+d>180°. Di qui a+b+c+d>360°, contraddicendo il fatto
che a+b+c+d= (a+d)+(b+c)=180°+180°=360°. |
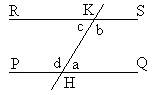
figura 3
|
Analogamente
si ha che è assurdo che la somma degli angoli interni che
stanno dalla stessa parte rispetto alla trasversale sia minore di
180°. 
|
Questa
dimostrazione non può essere corretta poiché non si usa
l'ipotesi che RS e PQ sono parallele. Quale errore ha
commesso Gigi?
Pierino, invece,
non riesce a capire dove è l'errore nella seguente
dimostrazione che 25=24, che ha trovato in un libretto di giochi
matematici:
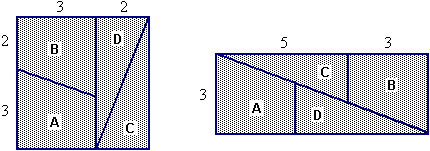
scompongo
un quadrato di lato 5 in due trapezi rettangoli uguali e in due
triangoli rettangoli uguali, nel modo illustrato in figura 4,
a sinistra; con dei movimenti posso trasportare le parti A, B, C e D
ottenendo il rettangolo raffigurato a destra.
Dov'è
l'errore?
figura
4
|
 |
Ritieni
che le difficoltà incontrate da Gigi e da Pierino in queste
due situazioni siano analoghe o siano legate problemi di tipo
differente?
Sai
trovare situazioni o attività di altro tipo che
possano essere impiegate didatticamente per mettere a fuoco i
problemi o esercitare le abilità che sono all'origine di
queste difficoltà?
Q6 Per
dimostrare che la somma degli angoli interni dei triangoli è
uguale a 180° si può procedere nel modo
seguente?
|
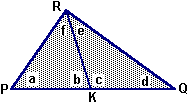
Sia
S la somma degli angoli interni dei triangoli. In figura 5
è raffigurato un generico triangolo.
Si ha:
a+b+f=S e c+d+e=S. Quindi a+b+f+c+d+e=2S.
Ma anche
a+d+e+f=S, mentre b+c=180°.
Quindi
S+180°=2S, da cui 180°=S.
 |
figura 5
|
Q7 Secondo
te:
(1) le dimostrazioni
nell'insegnamento devono essere un oggetto di attività
conoscitive o uno strumento conoscitivo?
(2) sono
culturalmente più significative attività volte a
seguire una dimostrazione, a trovare una dimostrazione, a
congetturare proprietà, o … ?
(3) tra le
dimostrazioni che hai studiato nella maggior parte dei corsi
universitari, le dimostrazioni della logica simbolica e le
dimostrazioni della cosiddetta geometria euclidea trovi delle
differenze?
(4) capire passo per
passo i procedimenti attraverso cui si svolge una dimostrazione ti
sembra che sia assimilabile al "capire" un programma (in un
linguaggio di programmazione) o alla attività del programma
traduttore (compilatore, interprete, …) che deve tradurre questo
programma in una sequenza di istruzioni macchina?
Q8 Come
ci si può assicurare che un sistema di assiomi per la
geometria definisca effettivamente qualcosa, cioè non porti a
contraddizioni?
|
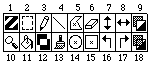
Q9 Un
semplice programma per realizzare disegni mediante computer è
dotato del "menu" raffigurato a lato: con un clic del
mouse in un riquadro si aziona il comando raffigurato
emblematicamente nel riquadro stesso. |
 |
Con altri comandi
azionabili da un menu a cascata è possibile comandare la
memorizzazione (Copy/Copia) e la riproduzione (Paste/Incolla) di
porzioni di schermo.
Ad
esempio il riquadro 1 consente di battere delle parti di testo
sul disegno.
2
consente di impiegare il mouse per "selezionare" una
porzione rettangolare del disegno sui cui poi operare con successivi
comandi.
3, 4,
5 e 6 consentono di usare il mouse per,
rispettivamente, tracciare linee a mano libera, tracciare segmenti,
tracciare poligonali, azionare una "gomma".
14 e 15
consentono di tracciare (descrivendo con il mouse il rettangolo che
li circoscrive) ellissi (cerchi con Shift premuto) o rettangoli
(quadrati con Shift).
7 e 8
ribaltano verticalmente o orizzontalmente quanto racchiuso nella
parte di schermo selezionata. 16 e 17 effettuano,
invece, una rotazione di 90° o di –90°.
9 fa sì
che il rettangolo selezionato e traslato mediante il mouse venga
sovrapposto "opacamente" al nuovo rettangolo su cui si è
posizionati (cioè cancelli le eventuali figure preesistenti),
18 fa sì che la sovrapposizione sia "trasparente".
|
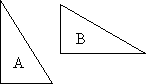
figura 6
|
Per
la realizzazione di un particolare disegno devo ottenere dalla
figura A la figura B, "inversamente uguale" (vedi figura
6).
Come
posso procedere dopo aver selezionato (vedi figura 7) la
figura A?
C'è
un'unica strada? |
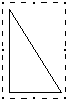
figura 7 |
Se invece devo
individuare il centro di un cerchio posso procedere per esempio nel
modo illustrato sotto:
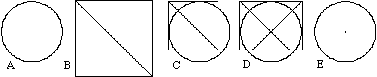
dato il cerchio (A),
traccio un quadrato capace di contenerlo e una sua diagonale (B),
seleziono una parte del quadrato che contenga un estremo e almeno
metà della diagonale, la copio e la incollo in trasparenza in
modo che i lati siano tangenti al cerchio (C), ne riproduco un'altra
copia, la ribalto orizzontalmente e la dispongo in modo che i lati
siano tangenti al cerchio (D), cancello le parti incollate sul
cerchio lasciando solo il punto di intersezione delle due diagonali
(E).
Secondo
te è più utile (didatticamente e culturalmente)
riflettere sulla conoscenze geometriche "incorporate" in
una / necessarie per usare una "vera"
applicazione per fare disegni o utilizzare del software specifico per
l'insegnamento della geometria euclidea (forse conosci qualche
prodotto di questo genere)?
Q10 Nell'appendice
3 è riprodotta la griglia per una lettura critica dei
"nuovi programmi" utilizzata in un corso di aggiornamento
sui nuovi programmi svoltosi nel 1992. Esamina i "nuovi
programmi" per il biennio e per il triennio, insieme ai
programmi della scuola media inferiore e ai "vecchi programmi"
(ad esempio dello scientifico) e, liberamente, o utilizzando la
griglia (riferendola alla geometria), cerca di mettere a fuoco
i principali problemi che comporta l'attuazione dei nuovi
programmi.
[Il fascicoletto distribuito agli insegnanti che avrebbero partecipato al corso conteneva, oltre ai quesiti, i programmi "Brocca" e "PNI" e gli altri programmi citati in Q10]
Appendice
1: dal manuale di Enriques e Amaldi
[Sono stati riportati, con alcune modifiche linguistiche inessenziali, solo una parte degli assiomi, delle definizioni e dei teoremi (includendo corollari e lemmi tra i "teoremi"), parte comunque sufficiente per affrontare Q3]
|
1 | |
ASS.
Per due punti A e B passa un'unica retta , che viene detta
retta AB. |
|
2 |
ASS.
Vi sono infinite rette. |
|
3 |
ASS.
I punti della retta sono ordinati secondo due versi opposti
e tali che in ciascuno di essi non vi è né primo né
ultimo punto e fra due punti vi sono infiniti punti intermedi. |
|
4 |
DEF.
Dati i punti A e B dicesi semiretta AB la parte della retta
AB che contiene A e i punti successivi nel verso secondo cui B
segue A. |
|
5 |
DEF.
Dati due punti A e B dicesi segmento AB la parte comune
alle semirette AB e BA. |
|
6 |
DEF.
Due segmenti aventi in comune un unico punto che è estremo
di entrambi si dicono consecutivi. |
|
7 |
DEF.
Dati due segmenti consecutivi AB e BC contenuti nella stessa
retta, il segmento AC si dice somma di AB e BC. AB dicesi
differenza di BC da AC. |
|
8 |
ASS.
L'uguaglianza tra segmenti è transitiva. Somme di
segmenti uguali sono uguali. Dati una semiretta AB e un segmento
CD, esiste un segmento AE uguale a CD e contenuto nella semiretta
AB. |
|
9 |
TEO.
L'operazione di somma tra segmenti è associativa e
commutativa |
|
10 |
TEO.
Differenze di segmenti uguali da segmenti uguali sono uguali |
|
11 |
ASS.
Dati due segmenti AB e AC, il primo contenuto nel secondo, esiste
un numero naturale n tale che, sommando ad AB n
segmenti uguali ad AB, si ottiene un segmento AD che contiene AC. |
|
12 |
ASS.
Una retta r determina due insiemi di punti, detti semipiani
limitati da r, tali che: r è contenuta in
entrambi i semipiani, ogni altro punto appartiene a uno solo di
essi, il segmento che ha per estremi due punti che non stanno su r
interseca r se e solo se i due punti appartengono a
semipiani diversi. |
|
13 |
DEF.
Dati tre punti A,B,C non allineati dicesi angolo [convesso]
ABC l'insieme dei punti comuni al semipiano limitato dalla retta
BA e contenente C e al semipiano limitato dalla retta BC e
contenente A. Le semirette BA e BC diconsi lati dell'angolo
ABC. |
|
14 |
DEF.
Se due rette AB e CD si intersecano in O gli angoli BOC e AOD si
dicono opposti al vertice. Due angoli con un lato in comune
si dicono consecutivi. |
|
15 |
DEF.
Dicesi somma di due angoli consecutivi AOB e BOC la figura
costituita dai punti dell'uno e dai punti dell'altro; AOB dicesi
angolo differenza di BOC da essa. Le figure ottenibili come
somma di angoli e che non sono angoli convessi vengono dette
angoli piatti se sono dei semipiani, angoli concavi
altrimenti. |
|
16 |
ASS.
L'uguaglianza tra angoli è transitiva. Somme
di angoli uguali sono uguali. Dati un angolo e una semiretta
esiste un'altra semiretta che con essa forma un angolo uguale
all'angolo dato. |
|
17 |
TEO.
Differenze di angoli uguali da angoli uguali sono uguali. |
|
18 |
ASS.
Gli angoli piatti sono uguali tra loro |
|
19 |
TEO.
Angoli opposti al vertice sono uguali. |
|
20 |
DEF.
Dati tre punti A,B,C non allineati dicesi triangolo ABC la
figura costituita dai punti comuni agli angoli CBA, ACB e BAC. |
|
21 |
DEF.
Due triangoli sono uguali se, indicati con A, B, C i
vertici del primo triangolo, è possibile prendere i vertici
del secondo nell'ordine A', B', C' in modo che i lati AB, BC e CA
e gli angoli in A, in B e in C siano ordinatamente uguali ai lati
A'B', B'C' e C'A' e agli angoli in A', in B' e in C'. |
|
22 |
ASS:
il primo criterio di eguaglianza tra triangoli. |
|
23 |
DEF.
Due rette si dicono parallele se non hanno punti in comune. |
|
24 |
DEF.
Una retta intersechi una seconda retta in P e una terza retta in
Q. Un angolo in P e un angolo in Q che contengano il segmento PQ e
stiano in semipiani opposti rispetto alla retta PQ diconsi
alterni interni. |
|
25 |
TEO.
Due rette intersecate in P e Q da una terza retta formando una
coppia di angoli alterni interni uguali sono parallele. |
|
26 |
ASS.
Esiste un'unica retta parallela a una retta data e passante per un
punto dato. |
|
27 |
TEO.
La relazione di parallelismo è transitiva. |
|
28 |
TEO.
Due rette parallele intersecate in P e Q da una terza retta
formano angoli alterni interni uguali. |
|
29 |
DEF.
Dato un punto O e un segmento OA, l'insieme dei punti P tali che
OP è uguale ad OA viene detto circonferenza di
centro O e raggio OA. |
|
30 |
DEF.
I punti dei raggi di una circonferenza che non appartengono alla
circonferenza stessa vengono detti punti interni ad essa. |
|
31 |
ASS.
Data una circonferenza e un punto A interno ad essa, ogni
semiretta di origine A ha un unico punto in comune con la
circonferenza. |
|
32 |
ASS.
Date due circonferenze a e b di centri A e B
distinti, siano AP un raggio di a contenuto nella semiretta
AB e BQ un raggio di b contenuto nella semiretta BA. Se P e
Q sono distinti e AP e BQ hanno QP come intersezione, a e
b hanno esattamente due punti in comune. |
|
33 |
ASS.
Se, per ogni numero naturale n, An+1Bn+1
è un segmento contenuto nel segmento AnBn,
allora esiste un punto P che, per ogni n, appartiene al
segmento AnBn. |
Appendice
2: dal manuale di Prodi
[Sono stati riportati, con alcune modifiche linguistiche inessenziali, solo una parte degli assiomi, delle definizioni e dei teoremi (includendo corollari e lemmi tra i "teoremi"), parte comunque sufficiente per affrontare Q3]
|
1 | |
ASS.
Esiste una distanza d [cioè una funzione d
che ad ogni coppia di punti associa un numero reale in modo che,
per ogni A, B e C:
•d(A,A)=0,
• d(A,B)>0 se B è
distinto da A, •
d(A,B)=d(B,A),
•
d(A,B)≤d(A,C)+d(C,B)]. |
|
2 |
ASS.
Per due punti A e B passa un'unica retta , che viene detta
retta AB. |
|
3 |
ASS.
Esistono tre punti A, B e C tali che C non appartiene alla retta
AB. |
|
4 |
DEF.
Due rette sono parallele tra loro se non hanno punti in
comune. |
|
5 |
ASS.
Ogni retta ammette una relazione d'ordine "<" e
queste relazioni d'ordine sono tali che: (A, B e C appartengono
alla stessa retta e (A<B<C o C<B<A)) se e solo se
d(A,C)=d(A,B)+d(C,D) |
|
6 |
DEF.
Dati due punti A e B, se A<B dicesi semiretta AB
l'insieme dei punti P tali che A<P e segmento AB
l'insieme dei punti P tali che A²P²B, se B<A
dicesi semiretta AB l'insieme dei punti P tali che P<A e
segmento AB l'insieme dei punti tali che B²P²A. |
|
7 |
ASS.
Per ogni semiretta di origine O e ogni numero reale positivo x
esiste un unico punto P della semiretta tale che d(O,P)=x |
|
8 |
ASS.
Per ogni retta r esistono due insiemi di punti disgiunti e
non contenenti r tali che un segmento AB non taglia r
se e solo se A e B appartengono al medesimo di tali insiemi (tali
insiemi diconsi semipiani di bordo r) |
|
9 |
DEF.
Si dice angolo ogni coppia di semirette a e b
aventi la stessa origine. Se a e b sono contenute
nella stessa retta, l'angolo viene detto piatto. Se a
e b non sono contenute nella stessa retta, viene chiamata
regione angolare di lati a e b l'intersezione
del semipiano che contiene a e ha bordo contenente b
con il semipiano che contiene b e ha bordo contenente a;
l'origine delle semirette viene chiamata vertice della
regione angolare. |
|
10 |
DEF.
Si dice triangolo ABC ogni terna di punti A, B e C non
appartenenti alla stessa retta. Si chiama regione triangolare
associata al triangolo ABC (o regione triangolare ABC)
l'intersezione delle tre regioni angolari aventi come lati le
semirette AB e AC, BA e BC, CA e CB. |
|
11 |
DEF.
Una isometria è una applicazione bigettiva F del
piano in sé stesso tale che per ogni coppia di punti A,B
d(A,B)=d(F(A),F(B)). |
|
12 |
TEO.
Una isometria trasforma una retta in una retta. |
|
13 |
DEF.
Data una retta r, una simmetria assiale di asse r
è una isometria F tale che se P sta in r allora
F(P)=P, altrimenti F(P) è dall'altra parte rispetto a r
e F(F(P))=P. |
|
14 |
ASS.
Per ogni retta esiste un'unica simmetria assiale che l'ha come
asse. |
|
15 |
DEF.
Una retta s è perpendicolare alla retta r
se è distinta da r e se viene trasformata in sé
dalla simmetria di asse r. |
|
16 |
TEO.
Dati un punto P e una retta r non passante per esso, esiste
un'unica retta perpendicolare a r e passante per P. |
|
17 |
DEF.
Dati un punto P e una retta r non passante per esso, dicesi
proiezione di P su r l'intersezione di r con
la retta perpendicolare a r e passante per P |
|
18 |
TEO.
Dati un punto P e una retta r non passante per esso, c'è
un solo punto di r che ha distanza minima da P, e è
la proiezione di P su r. |
|
19 |
TEO.
La relazione di perpendicolarità è simmetrica |
|
20 |
TEO.
Una qualunque isometria trasforma due rette tra loro
perpendicolari in due rette tra loro perpendicolari. |
|
21 |
ASS.
Data una retta r e un punto P di essa, esiste un'unica
retta perpendicolare a r e passante per P. |
|
22 |
TEO.
Due rette perpendicolari a una stessa retta sono tra loro
parallele. |
|
23 |
TEO.
Dati una retta r e un punto P, esiste una parallela a r
passante per P. |
|
24 |
DEF.
Dicesi simmetria centrale di centro O l'applicazione che
manda O in O e ogni altro punto P nel punto P' della semiretta PO
tale che d(O,P)=d(O,P'). |
|
25 |
TEO.
Componendo due simmetrie assiali con assi perpendicolari fra loro
si ottiene la simmetria centrale che ha come centro il loro punto
di incontro. |
|
26 |
TEO.
Una simmetria centrale è una isometria. |
|
27 |
TEO.
Una simmetria centrale trasforma una retta in una retta ad essa
parallela. |
|
28 |
ASS.
Se r e s sono rette che si incontrano in O, se
indichiamo con P un punto di r e con P' la sua proiezione
su s, si ha che d(O,P') è proporzionale a d(O,P). |
|
29 |
TEO.
È unica la parallela mandata a una retta da un punto ad
essa esterno. |
|
30 |
TEO.
La relazione di parallelismo è transitiva. |
|
31 |
TEO.
Dati due punti A, B di una retta r e due punti P,Q di una
retta s con d(A,B)=d(P,Q), fissati due semipiani a e
b con bordi, rispettivamente, r e s, esiste
un'unica isometria che manda A in P, B in Q e trasforma a
in b. |
|
32 |
ASS.
Esiste un'unica funzione M, detta misura angolare, che fa
corrispondere a ogni angolo (a,b) un numero reale
in modo che:
•
M(a,b)=0 se e solo se a=b, M(a,b)=π
se (a,b) è piatto, l'immagine di M è
[0,π],
• s e c
è una semiretta contenuta nella regione angolare (a,b)
e ha la stessa origine di a e b, allora
M(a,b)=M(a,c)+M(c,b),
•
M(a,b)=M(c,d) se (a,b) e
(c,d) sono isometrici. |
|
33 |
TEO.
M(a,b)=M(c,d) se e solo se (a,b)
e (c,d) sono isometrici. |
|
34 |
TEO:
primo criterio di eguaglianza (isometria) per i triangoli. |
Appendice
3: una griglia per la lettura dei nuovi programmi
La
griglia era stata usata per un'iniziativa sui programmi della scuola
secondaria superiore realizzata in collaborazione con il nucleo di
ricerca didattica Grem e con il Cidi. [Vedi: C.Dapueto & F.Furinghetti, "Un'esperienza di lettura critica dei Nuovi Programmi di Matematica per il primo biennio della scuola secondaria superiore", Insegnare, n.11-12, 1992]
Punti in
cui articolare la lettura di ciascuna area matematica
A) Uno
dei problemi di fondo per l'attuazione dei programmi è quello
del raccordo con la scuola media inferiore, che si può
articolare nei seguenti punti:
-
1) Ciò
che gli alunni dovrebbero sapere dalla scuola media (in relazione a
questa area).
-
2) Ciò
che (mediamente) sanno dalla scuola media.
-
3) Ciò
che l'insegnante ("standard") dà per scontato che
sappiano.
-
4) Che
cosa cambia, al riguardo, per chi svolge i "nuovi programmi".
B) Per
cogliere meglio il senso dei cambiamenti è utile
confrontare i programmi della Commissione Brocca sia con i
vecchi programmi che con quelli del P.N.I. (rispetto a questi ultimi,
alcuni temi sono stati riscritti rendendo meno esplicite le
innovazioni). Per valutare la direzione dei cambiamenti "reali"
nella pratica dell'insegnamento è utile tener conto di come
nuovi e vecchi programmi sono stati "interpretati" dai
libri di testo.
-
1) Cambiamenti
rispetto ai programmi vecchi (del Liceo Scientifico o di altra
scuola): che cosa resta, che cosa sparisce, che cosa viene
modificato (in questa area).
-
2) Confronto
tra "Brocca" e "P.N.I." (riguardo sia ai
contenuti che ai commenti).
-
3) "Interpretazione"
dei vecchi e dei nuovi programmi da parte dei libri di testo
(riguardo sia ai contenuti che alla loro impostazione).
C) Dalla
lettura del complesso dei programmi di matematica, da quelli per le
elementari fino a quelli per il 1° biennio della scuola
secondaria superiore, emerge l'indicazione di un insegnamento a
spirale: gli argomenti vengono man mano ripresi con
successivi livelli di approfondimento, formalizzazione e
integrazione con altre aree matematiche.
-
1) Aspetti
che, in questo senso, caratterizzano (in questa area contenutistica)
gli obiettivi del biennio superiore rispetto a quelli della scuola
media.
-
2) Alla
luce di quanto in 1), abilità e concetti da dare per
"scontati" e da "recuperare". Quanto questa
valutazione dipende dal tipo di scuola secondaria superiore.
D) Nei
nuovi programmi sono presenti avvertenze didattiche
(sia nella parte generale che in quella articolata per temi) relative
al modo in cui introdurre e sviluppare gli argomenti, anche al fine
di focalizzare meglio gli aspetti significativi della matematica e
delimitare il peso, nell'insegnamento e nella valutazione, degli
aspetti più nozionistici e fuorvianti.
-
1) Obiettivi
di apprendimento da perseguire (in sintesi) e cose "da non
fare" e metodi da non seguire (esempi). Eventuali perplessità
riguardo a queste indicazioni.
-
2) Come
accogliere (per quest'area contenutistica) l'indicazione di «partire
da situazioni didattiche che favoriscano l'insorgere di problemi
matematizzabili, …» (vedi il primo
capoverso delle "Indicazioni didattiche"): esempi.
E) Nei
programmi è data l'indicazione di non usare l'ordine di
presentazione dei temi come ordine di svolgimento ma di sviluppare
i temi in modo integrato.
-
Aspetti di questa
area contenutistica che possono essere sviluppati in maniera
integrata (risparmiando "tempo" e favorendo reciproche
"motivazioni") con quelli di altre aree contenutistiche o
del "laboratorio". Esempi e difficoltà a realizzare
questa integrazione.
Nota.
Il punto A1 della griglia è un po' ambiguo: si pone il
problema "dovrebbero sapere" rispetto a che cosa? (1) agli
obiettivi dei programmi della SMI o (2) alle esigenze della
SSS? Il problema in parte dipende dalla soluzione del nodo:
biennio come ultimo segmento della scuola dell'obbligo o no?
Comunque a noi è
parso che ci si debba riferire essenzialmente a (1): ogni livello
scolastico deve raccordarsi con quello precedente e deve tener conto
dei programmi ivi in vigore. Invece spesso accade che chi è
nel livello precedente si preoccupi (o sia indotto a preoccuparsi)
più che dei propri programmi di quello che potrebbe essere
preteso nel livello successivo. E` un problema che si ripropone ad
ogni passaggio di scuola o di ciclo (anche tra biennio e triennio).
In particolare spesso l'insegnante di SSS non conosce neanche i
programmi della SMI.
Del
resto la SMI deve fornire/sviluppare un bagaglio di conoscenze e di
"atteggiamenti" utile sia a chi conclude la scuola che a
chi prosegue gli studi. Quindi, affrontando A1 e A2, occorre tener
conto della propria esperienza con gli alunni delle classi prime per
individuare quali aspetti ritenuti prioritari dai programmi della SMI
sono scarsamente o malamente perseguiti e sarebbero invece importanti
per innestare l'insegnamento secondario superiore.
Seconda Parte