Q3  Vediamo come è possibile dimostrare il teorema (#) riferendosi alle presentazioni assiomatiche utilizzate nei manuali indicati, lasciando al lettore il confronto con quanto si può fare riferendosi ad altri manuali.

Possibile dimostrazione usando l'"Enriques-Amaldi": 

–    i due triangoli APX e YPB per ipotesi hanno AP=BP, XP=YP e hanno gli angoli in P uguali in quanto opposti al vertice; quindi, per il 1° criterio di eguaglianza, i due triangoli sono uguali; –    in particolare sono uguali gli angoli in A e in B; quindi, poiché questi angoli sono alterni interni rispetto alla coppia di rette AX e BY e alla loro trasversale AB, le rette AX e BY sono parallele; analogamente la retta BY è parallela alla retta CZ; –    quindi, per la transitività del parallelismo, AX è parallela a CZ.

Possibile dimostrazione usando il "Prodi" (seguendo l'impostazione di questo manuale, in (#) al posto di AB=BC, … si dovrebbe scrivere d(A,B)=d(B,C), … ):  –    sia A e B che X e Y si corrispondono nella simmetria centrale di centro P; –    poiché le simmetrie centrali trasformano ogni retta in una retta ad essa parallela, la retta AX è parallela alla retta BY; analogamente la retta BY è parallela alla retta CZ; –    quindi, per la transitività del parallelismo, la retta AX è parallela alla retta CZ.

Nota.  In entrambe le dimostrazioni non si sono utilizzate le ipotesi AB=YZ e XY=BC, che possono quindi essere eliminate. Anche il dispositivo a fianco, infatti, manterrebbe il contenitore verticale. Tuttavia questo dispositivo non si potrebbe richiudere completamente! Il parallelismo tra AX e CZ non esaurisce tutti gli aspetti del funzionamento del dispositivo.

    La seconda dimostrazione appare decisamente più semplice. Ma, per ora, abbiamo considerato solo la parte finale della dimostrazione "completa". Esaminiamo, dunque, l'intera dimostrazione.

    Nella pagina seguente, mediante due grafi ad albero, per ciascuna delle due impostazioni sono indicate le "cose" (tra assiomi (A), definizioni (D) e teoremi (T) elencati nelle appendici 1 e 2 della prima parte dell'articolo) necessarie per comprendere l'enunciato (En) e la dimostrazione (Dim) del teorema (#), le ulteriori "cose" necessarie per comprendere gli enunciati e (se si tratta di teoremi) le dimostrazioni di queste "cose", e così via.
    Abbiamo usato "…" al posto di sottografi in cui comparirebbero "cose" già richiamate. Per esempio la comprensione dell'enunciato di (#) richiede 5D (definizione di segmento) e 23D (definizione di parallelismo), e la definizione di retta AB, data all'interno di A1; ma A1 è già stato richiamato per la comprensione di 5D, per cui al suo posto si è messo "…".

Nota. Per la comprensione di (#) ci si è posti il problema di risalire ai significati di "segmento AB", "retta AB" e "parallelismo", non al significato di "uguaglianza", che non viene esplicitato con una definizione (è un concetto primitivo il cui uso nelle dimostrazioni viene regolato dagli assiomi, in particolare da: 8A, 16A, 18A, 22A), e al significato di "appartenenza", che viene assunto come noto (al pari di altri concetti insiemistici).
    La spiegazione del principio di funzionamento del dispositivo riferita a una di queste presentazioni assiomatiche indubbiamente non è accessibile a una persona "normale": si pensi alla lunghezza della dimostrazione completa di (#), alla complessità della rete di rimandi, collegamenti, … necessari (di cui danno un'immediata percezione i diagrammi della pagina precedente), … e anche alla scelta dei principi dati per evidenti o noti (assiomi). La spiegazione presentata discutendo Q1, basata su un ragionamento dinamico e che fa uso di sistemi di riferimento (assoluti e relativi), sembra decisamente più efficace.
    Tutto ciò sembra mettere in luce che le sistemazioni disciplinari non sempre offrono presentazioni "naturali" dei concetti che affrontano, sembra mettere in discussione il ruolo della dimostrazione come strumento conoscitivo, …. Prima di affrontare in termini generali le problematiche culturali e didattiche che si aprono, è utile affrontare le ulteriori riflessioni più "tecniche" proposte dai quesiti successivi.

Q4  Il punto (1) del quesito è da collegare al problema della motivazione alla attività di dimostrazione, e, in particolare, ai due seguenti aspetti: 
•   Nel caso di questo teorema, come nel caso di gran parte dei teoremi relativi a una presentazione assiomatica della geometria o ad altre teorie assiomatiche, la dimostrazione non si preoccupa tanto di certificare la verità di quanto affermato, quanto la sua deducibilità dalle cose prese per buone. In altre parole si vuole soprattutto verificare l'adeguatezza dei postulati alla "cattura" delle conoscenze che si vogliono inquadrare assiomaticamente. Ciò, tutto sommato, valeva per Euclide (che, sostanzialmente, ha riorganizzato conoscenze geometriche note e utilizzate da secoli) come vale per la matematica attuale; quello che cambia è il significato che si dà alle "conoscenze" (su questo aspetto ritorneremo successivamente). Senza un inquadramento culturale di questo ruolo delle dimostrazioni sono giustificate (anzi, dovute) le perplessità di Pierino.
•   Anche se questo criterio d'uguaglianza fosse affrontato in un'ottica diversa da quella di una presentazione assiomatica della geometria si porrebbe, comunque, la comprensione del suo significato culturale: a che serve? Si può osservare che la situazione didattica cambierebbe nettamente se il criterio fosse introdotto mediante il problema: "conoscendo un angolo e le misure dei due lati che ne hanno il vertice come estremo, sono in grado di riprodurre il triangolo in una qualunque posizione del piano?", o, quanto meno, se non si disegnasse completamente il secondo triangolo. Questo secondo aspetto del problema della motivazione, essenzialmente legato all'uso di tecniche didattiche più o meno appropriate, è più facilmente abbordabile. 
    L'insoddisfazione di Pierino (o di una qualunque persona che cerchi onestamente di capire il ragionamento condotto dal libro) presentata nel punto (2) nasce probabilmente dalla banalità dell'argomentazione condotta e dal fatto che essa non sembra far riferimento ad assiomi o ad altri teoremi già dimostrati. Insomma, non sembra una dimostrazione.
    A un'analisi più approfondita ci si accorge che la dimostrazione è un piccolo imbroglio: dal fatto che esistono un movimento M1 che trasforma ∠M in ∠A, un movimento M2 che trasforma il segmento MN nel segmento AB e un movimento M3 che trasforma il segmento MP nel segmento AC, non si può dedurre che esiste un "movimento" (M1 o un altro) che fa tutte e tre le cose.
    Dietro alle perplessità di Pierino (e alle difficoltà degli autori dei libri di testo) probabilmente si possono individuare anche questioni più generali legati alla natura della geometria: le figure sono corpi o parti di spazio? i punti sono punti materiali o posizioni? che cosa sono i movimenti rigidi? …, e al significato di eguaglianza: le figure (definite come insiemi di punti) sono uguali come insiemi o come figure? che vuol dire mettere in corrispondenza? …. Sono questioni che vengono eluse dalle presentazioni della geometria che non mettono in luce il concetto di modello matematico, usano un lessico inadeguato (es.: "movimento rigido" invece di "movimento" come modello matematico dello spostamento di un corpo rigido), non fanno confronti tra i diversi significati che un termine può assumere in contesti diversi, …
    Con un "ragionamento" simile a quello impiegato nel libro per il 1° criterio e con qualche difficoltà in meno (invece delle semirette AB, AC, … ho già i segmenti) potrei "dimostrare" il 3° criterio, che, poi, è forse quello più "intuitivo" e che richiede concetti che appaiono come più elementari. Anche le perplessità di Pierino considerate nel punto (3) sono giustificate: il libro di testo non ha delimitato il (ovvero, non ha esplicitato assiomaticamente la portata del) concetto di movimento: le proprietà che i movimenti conservano, il modo in cui possono essere composti, … ; ne ha fatto un uso illecito nella dimostrazione del 1° criterio inducendo una confusione tra spiegazioni "fisiche" e argomentazioni "matematiche".

Q5  L'errore di Gigi è di tipo logico:
la negazione di:		comunque prenda a e b angoli interni dalla stessa parte rispetto a HK, a+b=180°
è:		esistono a e b angoli interni … tali che a+b≠180°
non:		(comunque prenda a e b angoli interni …, a+b>180°) oppure (comunque prenda a e b angoli interni …, a+b<180°)
[e neanche:  comunque prenda a e b angoli interni …, a+b≠180° ]

    L'errore che non riesce a trovare Pierino è il fatto che le quattro sottofigure possono essere ricomposte, senza buchi o sovrapposizioni, in un rettangolo di dimensioni 3 e 8 solo se α (e β) è uguale a γ (e a δ), e la verifica di questa condizione nella dimostrazione viene trascurata. Se effettuo la scomposizione e la ricomposizione concretamente, con carta e forbici, posso verificare che le quattro figure si sovrappongono:

    Senza operare con carta e forbici basta osservare che la pendenza del lato obliquo del trapezio rispetto al lato opposto (1/3) è diversa da quella dell'ipotenusa del triangolo rispetto al cateto maggiore (2/5) e che, quindi, se unisco trapezio e triangolo nel modo suggerito, lato obliquo del trapezio e ipotenusa non si allineano.
    La difficoltà di Pierino è seguire la dimostrazione senza giustificare passaggi in base all'intuizione "sensibile" (a una prima vista α e γ sembrano uguali).
     Il ricorso (ingannevole – come in questo caso – o non giustificato dagli assiomi – come nel caso di Q4) all'intuizione sensibile si combina spesso a un'altra fonte di difficoltà: il fatto che, per illustrare proprietà o agevolare lo svolgimento o la comprensione delle dimostrazioni, si disegnano delle figure che sono casi particolari. Vediamo due esempi tipici, in contesti didattici diversi. 
•   Un libro di testo illustra il "teorema dell'angolo esterno" nel modo raffigurato sotto a destra. Per facilitare la comprensione del teorema il triangolo e i due angoli sono stati scelti in modo che l'angolo esterno (colore scuro) sia evidentemente maggiore dell'angolo interno (colore chiaro). Ma questa è una scelta didattica disastrosa: in questo modo si demotivano gli studenti all'attività dimostrativa. Sarebbe stato molto più significativo ed efficace considerare, eventualmente accanto alla precedente figura, la figura a sinistra, in cui alla vista, senza ragionamenti o misure accurate, non è facile confrontare l'ampiezza dei due angoli. •   Nella dimostrazione che l'area di un triangolo è metà dell'area del rettangolo che ha un lato coincidente con un lato L del triangolo e un altro lato uguale all'altezza del triangolo relativa a L, è facile incorrere nell'errore di limitarsi a considerare una situazione (vedi figura seguente) del tipo A: piede dell'altezza interno al lato; se si è più accorti si può considerare anche la situazione B, affrontabile dimostrando, mediante una somma di triangoli uguali, che parallelogramma e rettangolo sono equiestesi; ma anche questo è un caso particolare: c'è anche la situazione C (proiezione del lato superiore esterna al lato inferiore).  Nota. Per inciso, osserviamo che per affrontare il caso C e, più in generale, per dimostrare l'equiestensione di due parallelogrammi α e β con due lati coincidenti e lati opposti allineati ma disgiunti, oltre che procedendo per scomposizioni e ricomposizioni più complesse di quella operata nel caso B, si può procedere più "dinamicamente" spostando il lato superiore di α lungo la sua retta di appoggio: il parallelogramma man mano si trasforma in un altro parallelogramma a cui è possibile applicare la scomposizione/ricomposizione usata nel caso B. Più formalmente, si tratta di considerare (utilizzando implicitamente la proprietà archimedea) una successione di parallelogrammi γ₁,γ₂,…,γ_n (con α e β come γ₁ e γ_n) tale γ_i e γ_i+1 abbiano lati superiori non disgiunti (nel caso seguente n=4):  Procedimenti "dinamici" di questo tipo si possono utilizzare anche al posto di altre dimostrazioni che, tradizionalmente, sono svolte attraverso sottodimostrazioni "caso per caso" ciascuna basata su una costruzione geometrica diversa dall'altra.

Q6  Come è noto, le proprietà angolari dei poligoni vengono studiate utilizzando il postulato delle parallele. In questa dimostrazione non se ne fa uso, quindi c'è qualcosa che non va. Analizzando più a fondo la dimostrazione ci si accorge che si è utilizzata implicitamente l'ipotesi che la somma degli angoli interni non dipenda dal particolare triangolo. E, in effetti, questa proprietà è equivalente (supposti gli assiomi di collegamento, ordinamento e congruenza) sia al teorema che si vuole dimostrare che al postulato delle parallele.

    Q5 e Q6 hanno messo in luce che, oltre alla difficoltà di comprendere il ruolo delle dimostrazioni in una sistemazione assiomatica della geometria, vi sono anche difficoltà "tecniche" a capire o condurre una particolare dimostrazione: di tipo logico-linguistico, o connesse al ricorso (spesso ingannevole) all'intuizione "sensibile", o che nascono quando per illustrare un teorema relativo a una classe di figure si disegna una particolare figura che inevitabilmente ha proprietà che non sono presenti nell'ipotesi del teorema, o che sono comunque legate al problema di non utilizzare implicitamente proprietà che non sono state dimostrate.
    Sia le difficoltà di tipo logico-linguistico che quelle di controllo delle proprietà che si impiegano sono comuni a tutte le aree matematiche, ma le difficoltà del secondo tipo sono presenti in modo particolare nel caso della geometria. Cerchiamo di approfondire che cosa è all'origine di ciò.
    A tal fine (e anche per avere qualche punto di riferimento per valutare le diverse impostazioni dell'insegnamento della geometria presenti nei libri) è utile fare una rapidissima "storia della geometria".

    Già diversi secoli prima di Euclide, presso Egizi, Babilonesi, Indiani, …, una discreta parte delle proprietà geometriche enunciate nei suoi Elementi erano utilizzate nella pratica, per misurazioni, costruzioni, studi astronomici, … . La fiducia in queste proprietà era fondata essenzialmente o sulla loro evidenza (nei casi più "semplici") o su considerazioni sperimentali.
    Presso i Greci si incomincia a dare un'organizzazione razionale alle conoscenze geometriche, nell'ambito di una speculazione filosofica sulla natura delle cose e, in particolare, dello spazio cosmico. Ecco qualche tappa: 
• i Pitagorici (500 a.C.), che, concependo il "punto" come corpuscolo elementare indivisibile e le figure come quantità finite di punti, tentarono di dare una trattazione aritmetica della geometria, articolata, anche se non organicamente, in postulati (principi ritenuti evidenti) e dimostrazioni;
• la "crisi" dovuta alla scoperta di lunghezze incommensurabili;^*

* È una crisi "filosofica", non "matematica", legata allo studio "fisico" dello spazio come entità cosmica, non come spazio astratto, e che ci è difficile comprendere. Nei libri di testo se ne trovano invece spesso presentazioni banalizzate o caricaturali, così come accade per i paradossi di Zenone, ridotti spesso a un problema di serie convergenti

• la distinzione in Democrito tra particelle elementari (di dimensioni finite, ma varie) e "punti-posizione", e i suoi metodi infinitesimali per calcolare estensioni (a cui poi Eudosso ha dato una sistemazione "∀ε∃"), e il "punto" come idea in Platone (400 a.C.);
• l'ordinamento logico delle scienze descritto da Aristotele: definizioni che associano un nome a un "ente", nel senso di cosa – oggetto o idea – che esiste, che è "reale"; nozioni comuni (o assiomi) che indicano alcuni principi generali comuni a tutte le scienze; postulati che indicano alcune proprietà evidenti da cui si vogliono dedurre le altre proprietà della scienza che si vuole ordinare;
• la realizzazione di questo ordinamento nel caso della scienza che si occupa dello spazio: la trattazione della geometria negli Elementi di Euclide (300 a.C.), che riorganizza e integra gli studi compiuti nei secoli precedenti.

    Nell'appendice 1 abbiamo riprodotto un'estratto della presentazione della geometria fatta negli Elementi di Euclide.
    Come si può osservare, Def1-14 non sono definizioni in senso matematico, sono solo – in accordo con Aristotele – delle assegnazioni di un nome a enti che vengono "individuati" appoggiandosi a concetti il cui significato è lasciato all'intuizione e al linguaggio comune ("lunghezza", "inclinazione", "giace uniformemente", …); la descrizione può non essere perfetta, ma tali enti esistono. Def15-20 sono invece abbastanza simili alle definizioni-abbreviazioni della matematica ("essere un triangolo equilatero" per "essere un triangolo e avere i lati uguali"). Si notino, inoltre, le differenze rispetto ai termini geometrici odierni: linea come arco di linea (Def3, Post1, …), distanza come segmento particolare (Post3), … e l'ottica costruttiva di Post1-3, che garantiscono la possibilità di effettuare alcune "operazioni".
    Per meglio comprendere l'impostazione degli Elementi di Euclide, analizziamo le dimostrazioni di due proposizioni (Prop), riportate in appendice (riscritte con un lessico moderno). 
    Osserviamo che nella dimostrazione di Prop1 il passo 3) non sembra giustificato: non c'è alcun postulato che, date due circonferenze soddisfacenti opportune condizioni, garantisca l'esistenza di punti comuni a entrambe (in determinate condizioni è garantita, da Post 5, solo l'intersezione di rette). 
    Nella dimostrazione di Prop4 al passo 1) si esegue un'operazione di "trasporto" di figure la cui possibilità non viene postulata. Per altro ciò appare in contraddizione con il procedimento complesso (di 12 passi, non riportato) con cui viene dimostrata Prop2, teorema che vuole certificare la possibilità di trasportare segmenti. Anche il passo 5) lascia perplessi, a meno che, dati due punti, Post1 assicuri, oltre all'esistenza, anche l'unicità del segmento che li ha per estremi.

    Nei secoli successivi gli Elementi sono stati oggetti di uno studio intenso (costellato da errori simili a quelli descritti in Q5 e Q6), soprattutto nel tentativo di dimostrare Post5 a partire dagli altri assiomi o di sostituirlo con un altro postulato più evidente, ma si deve arrivare al seconda metà del XIX secolo perché si comincino a mettere a fuoco le "carenze" della presentazione euclidea a cui abbiamo accennato sopra. Deve infatti farsi strada l'idea della geometria come studio degli spazi astratti, che usi definizioni e dimostrazioni che non ricorrano a concetti e argomentazioni di "fisica".
    Un contributo in questo senso era già stato dato dall'ideazione della geometria analitica (Cartesio e Fermat, XVII secolo), con cui erano stati fusi due metodi noti sin dall'antichità, l'impiego dell'algebra in geometria e l'uso delle coordinate, per dare una definizione "numerica" dello spazio e dei concetti geometrici di base.
    Nella prima metà dell'Ottocento si dimostrò l'indipendenza di Post5 dagli altri postulati e si prospettò la possibilità di sviluppare le cosiddette geometrie non euclidee, ma questi studi rimasero del tutto marginali nella comunità scientifica.
    È nella seconda metà dell'Ottocento che (in relazione all'estendersi degli ambiti di applicazione della matematica conseguente agli sviluppi tecnologici e ai mutamenti nell'organizzazione economica) si precisa l'esigenza di dare una fondazione autonoma alla matematica. Inizialmente ciò accade in riferimento all'analisi matematica: fino ad allora la definizione delle operazioni e le proprietà dei numeri reali erano fondate su considerazioni fisiche (la geometria intesa alla Euclide), non ci si preoccupava di definire che cos'è una funzione (che veniva intesa come la descrizione di una "legge" che lega una grandezza fisica a un'altra grandezza), … .
    Diventa man mano chiara la necessità di definire i modelli matematici indipendentemente dai contesti, di usare linguaggi formali con una sintassi e una semantica più rigorose di quelle delle lingue naturali, … al fine di consentire l'applicazione della matematica ai più vari fenomeni, di rendere più controllabili le dimostrazioni e, quindi, più sicuro l'impiego della matematica, … e di favorire lo sviluppo stesso della matematica (facilitare le generalizzazioni, l'individuazione di analogie tra aree matematiche diverse, l'interpretazione di una teoria in altre, …).

    È in questo ambito che viene messa a fuoco la concezione moderna dei sistemi assiomatici e che, tornando alla geometria, si arriva alle prime presentazioni "matematiche" di tipo assiomatico della geometria, di cui la più rigorosa e, nel contempo, con un'articolazione più vicina agli elementi di Euclide, è quella messa a punto da Hilbert (1899): vedi appendice 2.
    L'introduzione che Hilbert premette all'elencazione degli assiomi («Consideriamo tre diversi sistemi di oggetti …») chiarisce la natura del metodo assiomatico matematico, ma viene oscurata dal modo in cui sono stesi gli assiomi: per venire incontro alle difficoltà dei suoi contemporanei di fronte all'uso del linguaggio simbolico, i termini e le relazioni primitive vengono descritte ricorrendo a parole del linguaggio naturale, spesso sostituite con sinonimi o parafrasi, col rischio di far perdere al lettore la natura astratta della formulazione, cioè la profonda differenza dalla presentazione assiomatica di Euclide. Per cogliere meglio questo aspetto può essere utile riscrivere gli assiomi usando dei simboli: 
–    il simbolo ε per indicare la relazione "giacere": ε(A,a) sta per "A giace su a"
–    il simbolo τ per indicare la relazione "fra": τ(A,B,C) sta per "B sta fra A e C"
–    il simbolo ≈ per indicare la relazione "… è congruente a …" 
    Gli assiomi di collegamento caratterizzano "ε". Ad esempio I.3 può essere riformulato così: «Data a, esistono A e B distinti tali che ε(A,a) e ε(B,a), ed esiste c tale che non ε(C,a)».
    Gli assiomi di ordinamento caratterizzano τ. Ad esempio II.1 può essere riscritto così: «Se τ(A,B,C), allora A, B e C sono distinti, τ(C,B,A) ed esiste a tale che ε(A,a), ε(B,a) e ε(C,a)».
    Gli assiomi di congruenza, ovviamente, caratterizzano il simbolo ≈.

    A questo punto possiamo chiarire meglio perché le dimostrazioni nell'ambito di una presentazione assiomatica della geometria sono più "esposte" all'utilizzo implicito di proprietà non ancora dimostrate: si usano gli stessi termini (punto, retta, segmento, …) impiegati per descrivere il concetto intuitivo di spazio che si vuole caratterizzare assiomaticamente, e, quasi con un circolo vizioso, si ricorre a questo (sotto forma di disegni) anche per guidare le dimostrazioni .
    Il rischio è più attenuato nel caso di sistemi di assiomi che non vogliono caratterizzare un unico "oggetto matematico", ma concetti, classi di oggetti, come nei casi degli assiomi dei gruppi, della definizione di distanza, di probabilità, …. In questi ambiti è più chiaro anche il ruolo della dimostrazione a partire degli assiomi: si vogliono individuare delle proprietà che valgono per tutti gli oggetti che verificano gli assiomi.
    I libri impostati come quello di Q4 hanno un'introduzione che fa più o meno riferimento alla concezione matematica dei sistemi assiomatici (quella descritta da Hilbert nella premessa), ma, poi, hanno uno svolgimento "alla Euclide" (il 1° criterio di eguaglianza dei triangoli non è assunto come assioma, come fa Hilbert, ma è dimostrato riproducendo, malamente, la dimostrazione euclidea di Prop4): per Euclide i concetti e i procedimenti impiegati traevano comunque giustificazioni dalla loro realtà nel "mondo delle idee", nel caso di questi libri "dimostrazioni" come quella riportata oscurano il ruolo della matematica, la natura dei modelli matematici.
    A questo punto sospendiamo la panoramica storica, che riprenderemo affrontando Q8.

Q7  Incominciamo dal punto (4) del quesito, ponendoci il problema:
    Che cosa vuole dire "capire" il seguente programma?

PRINT "Introduci M,N interi positivi non superiori a 40" INPUT M, n FOR r = 1 TO M : FOR c = 1 TO N   LOCATE r, c   IF c=1 OR c=N OR r=1 OR r=M THEN PRINT "I" ELSE PRINT "O" NEXT : NEXT

[LOCATE r,c posiziona la "penna" del computer nella riga ra, alla ca colonna]

• Saper eseguire passo per passo le azioni che vengono comandate al computer? o • Prevedere che il programma dà luogo alla stampa di una figura simile a quella a fianco?

IIIIIIIII IOOOOOOOI IOOOOOOOI IOOOOOOOI IIIIIIIII

    A tutti pare ovvio che la risposta corretta sia la seconda. Ma, se facciamo una trasposizione dai programmi alle dimostrazioni, ci si rende conto di una cosa forse meno ovvia: spesso, a scuola (e nei corsi universitari, in cui gli insegnanti - e i ricercatori - sono formati …) non si fanno "capire" le dimostrazioni agli alunni: 
–   per usare termini già usati dagli antichi greci, si presenta loro la sintesi della dimostrazione senza l'analisi (come ricondurre la proposizione [il problema] ad altre già dimostrate [risolti] o che appaiono più agevoli da dimostrare [risolvere]?), 
–   sono assenti, o rare, attività in cui vengono congetturate proprietà, in cui vengono formulati problemi («è indispensabile che le aste siano incernierate a metà affinché il dispositivo di Q1 funzioni?»), in cui si sperimentano proprietà, … 
–   non viene chiarita (storicamente o riferendosi ai nostri giorni) la distinzione tra le fasi della ideazione, costruzione, … dei "contenuti" della matematica e quelle della loro sistemazione e della loro esposizione; 
–   nel dare molto spazio ad attività dimostrative riferite a teoremi "classici", nel proporre la dimostrazione come "strumento" attraverso cui costruire le conoscenze degli alunni invece che come "oggetto" di studio, … si dà quindi anche un'immagine distorta del lavoro dei matematici (che, per altro, in genere non esaminano le dimostrazioni dei teoremi che utilizzano, a meno che non pensino di ricavarne una comprensione più profonda del teorema, trarne spunti per generalizzazioni, individuare strategie applicabili in altri contesti, …)^*

* Sarebbe un po' come dire che è attraverso gli esperimenti che sono state messe a punto le leggi della fisica, come sostenere che gli alunni devono imparare la fisica attraverso gli esperimenti, come pensare che un fisico riproduca gli esperimenti con cui è stata convalidata una legge prima di utilizzarla nella sua attività …

    Più avanti daremo indicazioni bibliografiche per l'approfondimento di tali aspetti.^*

* Si vedano in particolare [5] e [11]. A proposito del punto (3) del quesito, che potrebbe aprire una riflessione più ampia su natura e ruolo delle dimostrazioni, qui ci limitiamo a una breve annotazione:  le dimostrazioni più comunemente svolte in un corso universitario integrano tecniche e proprietà riferite a varie aree matematiche, ricorrono a interpretazioni di una teoria matematica in un'altra (dimostrazioni di analisi che ricorrono alla geometria, di teoria dei numeri che ricorrono alla variabile complessa, …), …; all'opposto, le derivazioni della logica simbolica sono totalmente sintattiche, si presentano come una successione di applicazioni di regole di riscrittura di espressioni

Q8  Per dimostrare la non contradditorietà del suo sistema di assiomi Hilbert ha dimostrato che lo "spazio cartesiano" ne è un modello, cioè che l'interpretazione degli assiomi nello spazio cartesiano (nel caso piano: punti come coppie di numeri reali; rette come equazioni di primo grado; "giacere su …" come verificare l'equazione …; …) dà luogo a proposizioni vere. In altre parole si è ricondotto alla geometria analitica.
    Ma, dato che era già chiaro da qualche decennio come definire i numeri reali autonomamente dalla fisica (attraverso successive costruzioni algebriche a partire dai numeri naturali o precisando il concetto di numero decimale illimitato) e che quindi era soddisfacente una presentazione analitica dello "spazio euclideo", quale necessità c'era di darne anche una definizione assiomatica? 
    Hilbert voleva dare una forma rigorosa alla presentazione assiomatica di Euclide, cioè dare una presentazione del concetto di spazio che fosse il più possibile in termini puramente geometrici. Non a caso nei primi quattro gruppi di assiomi non intervengono neanche concetti insiemistici (l'"appartenenza" non è quella insiemistica, ma è regolata da specifici assiomi) e solo nell'ultimo gruppo di assiomi interviene il concetto di numero naturale.^*

* La versione di V.2 data in appendice riproduce, sostanzialmente, la formulazione della completezza per i numeri reali; quella originale era: «un modello della "geometria piana" è un modello di I, II, III, V.1 tale da non ammettere alcuna estensione propria che verifichi I, II, III, V.1» (un modello della "geometria piana euclidea" deve verificare anche IV); è una versione più difficile per il lettore non "allenato" (non è un assioma in senso stretto) ma più "autonoma" dal concetto di numero reale

    Ciò non solo per fini storico-critici. Attraverso una opportuna scelta dei concetti primitivi e delle proprietà che li caratterizzano, Hilbert voleva rendere chiara la portata dei vari assiomi, dar modo (con tagli e aggiunte che garantissero la categoricità del sistema – esistenza di unico modello a meno di isomorfismi) di definire altri concetti matematici di spazio, …^*

* Gli assiomi di Hilbert sono anche indipendenti ciascuno dai rimanenti; ciò è utile per studiare la portata dei vari assiomi; didatticamente, per semplificare le dimostrazioni, può a volte essere utile trascurare questo aspetto

    A scuola, in genere, si perdono tutti questi aspetti, sostanziali, di una presentazione assiomatica della geometria (quali finalità ha? definisce effettivamente qualcosa? definisce un'unica cosa? …). Sia la significatività che la correttezza di una definizione dipendono dal contesto culturale: non possiamo criticare con gli occhi di oggi la significatività e la correttezza degli Elementi di Euclide, così come è difficile pensare che si possa dare una definizione assiomatica della geometria (oggi accettabile come corretta e significativa) agli studenti della scuola secondaria superiore, che non hanno gli strumenti culturali per affrontarla.^*

* così come non si vede che valenza culturale possa avere - e come possa essere portata a termine correttamente - la costruzione di R (o anche solo di Q) a partire da N, senza inquadrarla storicamente nel tentativo di fondare tutta la matematica sull'aritmetica e di dimostrare sintatticamente la non contradditorietà di una presentazione assiomatica di quest'ultima.

    A questo punto è utile completare la panoramica storica con qualche cenno a varianti o alternative alla presentazione assiomatica hilbertiana. 
    Una prima variante è quella che fa ricorso alla teoria degli insiemi: le figure geometriche vengono interpretate come insiemi di punti e sono soggette alle usuali operazioni e relazioni insiemistiche (appartenenza, inclusione, intersezione, unione, …). Si vedano, per esempio, gli assiomi dell'"Enriques-Amaldi", nella prima parte dell'articolo (si noti, in particolare, che l'assioma di Pasch – II.4 – viene sostituito da quello che abbiamo indicato come 12-ASS, noto come assioma di separazione). 
    Un'ulteriore variante è quella di assumere come primitivo non il concetto di congruenza, ma quello di movimento. Al posto degli assiomi di congruenza abbiamo (nel caso piano):

1)	I movimenti del piano sono funzioni bigettive dal piano nel piano che (rispetto alla composizione di funzioni) costituiscono un gruppo.
2)	Se f è un movimento e s è una semiretta di origine A, f(s) è una semiretta di origine f(A).
3)	Se in un movimento restano fermi tre punti non allineati, tutti i punti restano fermi, cioè il movimento è la funzione identità.

e la definizione:  due figure sono congruenti quando esiste un movimento che trasformi l'una nell'altra. 
    Questi (o altri equivalenti) sono gli assiomi mancanti nel libro di testo di Q4.

    Le presentazioni fin qui discusse vengono a volte chiamate sintetiche, per distinguerle dalle presentazioni che fanno ricorso al concetto di numero reale, che possono essere puramente analitiche (punti come n-uple di numeri reali) o ricorrere alla struttura dei numeri reali solo per semplificare l'ordinamento della retta e l'introduzione della continuità.
    Queste seconde presentazioni, decisamente "ibride", di cui si è iniziato a fare uso negli anni trenta, vengono usualmente descritte come approccio metrico alla geometria. Come concetti primitivi si considerano due funzioni a valori in [0,∞): 
d,  avente come argomenti le coppie di punti, con gli assiomi che la caratterizzano come distanza e l'assioma del righello (per ogni retta r esiste f: r → R bigettiva tale che d(A,B) = | f(A) - f(B) | per ogni A,B∈r), 
m,  avente per argomenti gli angoli (intesi come coppie di semirette con origine comune), con assiomi che la caratterizzano come misura angolare (sostanzialmente dando una rappresentazione astratta delle caratteristiche del goniometro). 
    Il postulato del righello, che, in pratica, dota la retta di un sistema di coordinate, consente di definire la relazione "C sta tra A e B" come "A, B e C sono allineati e d(AB) + d(BC) = d(AC)". È evidente come la congruenza sia riconducibile a d e m. 
    La continuità della retta è "scaricata" su R. 
    È abbastanza facile dimostrare sia il teorema "Retta-cerchio" (esistenza di due punti comuni a un cerchio e a una retta che abbia un punto esterno e uno interno al cerchio) che il teorema "Due-cerchi" (esistenza di due punti comuni a due cerchi aventi la distanza fra i rispettivi centri minore della somma dei rispettivi raggi: proprietà utilizzata implicitamente da Euclide dimostrando Prop1).
    Questi teoremi sono di più difficile dimostrazione in una trattazione sintetica. Vi sono, dunque, anche assiomatizzazioni di tipo sintetico in cui al posto dell'assioma di completezza vengono assunti come assiomi i due teoremi stessi. In questo modo, tuttavia, si perde la categoricità del sistema assiomatico ^* (l'"Enriques-Amaldi" introduce questi due assiomi per affrontare la costruzione di perpendicolari, trasporti di angoli, …, rinviando a un secondo momento, per affrontare il concetto di misura, l'introduzione dell'assioma di completezza).

* Con tale sostituzione il sistema ha come modello sia l'usuale piano cartesiano che quello che si ottiene rimpiazzando R con l'insieme I così definito:  1∈I; se a∈I allora √(1+a²)∈I; se a,b∈I allora a+b, a-b, a·b e (se b≠0) a/b sono elementi di I

    Vi sono molti libri di testo che utilizzano l'approccio metrico, ma quasi tutti (non il "Prodi": vedi 5-ASS) con errori grossolani. Ecco due tipici esempi: 
•  il postulato della continuità presentato come: «esiste una corrispondenza biunivoca tra la retta e R», non mediante l'assioma del righello o simili, senza stabilire collegamenti con la metrica, consentendo che la retta sia zeppa di "buchi" e che sia "limitata" (a volte si aggiunge l'assioma "ogni retta è illimitata in entrambi i sensi", ma senza spiegare che cosa voglia dire "illimitata"); 
•    la lunghezza presentata, dopo aver introdotto i concetti di distanza e di isometria, come «quel "quid" che accomuna i segmenti che appartengono a una stessa classe di equivalenza, associata alla relazione di isometria», mescolando, rozzamente («quel "quid" …), approccio sintetico e approccio metrico: in un approccio sintetico ha senso introdurre la lunghezza come classe di equivalenza di segmenti congruenti, non ha alcun senso farlo se si dispone già del concetto di distanza. 

    Negli anni sessanta sono state proposte alcune "eleganti" caratterizzazioni puramente algebriche della geometria. Famose sono quella proposta da Blumenthal (lo spazio euclideo come spazio metrico completo, dotato di un determinante opportunamente definito, che verifica quattro assiomi dalla formulazione molto "semplice") e, soprattutto, quella proposta da Dieudonné: il piano [lo spazio] euclideo come spazio vettoriale su R munito di un prodotto scalare × (la distanza tra P e Q diventa √((P-Q)×(P-Q))). 
    Anche queste sono formulazioni equivalenti a quelle di Hilbert, ma … si perde ogni collegamento diretto con l'intuizione spaziale. La presentazione di Dieudonné è particolarmente economica e è indubbiamente significativa nell'ambito di in un corso universitario, ma, ahimè, Dieudonné, col motto «abbasso Euclide» la propose come punto di riferimento per l'insegnamento nella scuola secondaria! 
    Choquet, negli stessi anni, cercò di realizzare un compromesso tra la geometria intesa come struttura algebrica e la geometria "classica", definendo i vettori e il prodotto scalare non assiomaticamente, ma a partire da assiomi più "geometrici":
–   postulati di incidenza e di ordine (sostanzialmente il I, il II e il IV gruppo di assiomi di Hilbert),
–   postulati di struttura affine (sostanzialmente, il postulato del righello e il "teorema di Talete"), e definizione dei vettori,
–   postulati di struttura metrica (assiomi che caratterizzano la nozione di perpendicolarità), e definizione del prodotto scalare. 
   La presentazione assiomatica di "Prodi" può essere considerata una variante del sistema proposto da Choquet che cerca di ridurne i formalismi e accentuare i collegamenti con l'intuizione spaziale. Una differenza che val la pena di sottolineare è la definizione di angolo. Choquet, dopo aver criticato le usuali definizioni di angolo, propone un'altra definizione o, meglio, definisce un'altra cosa: chiama angoli in P non delle figure, ma le rotazioni di centro P (cioè le isometrie che lasciano fisso il solo punto P), e lo fa dopo uno studio sistematico delle isometrie. Prodi, invece, anticipa la definizione di angolo, che dà "alla Hilbert", come coppia di semirette. 
    Vi sono diversi libri di testo che si sono ispirati alle proposte di Choquet, ma anche in questo caso spesso con errori abbastanza vistosi. Tipico è quello di far seguire alla definizione di angolo come rotazione (alla Choquet, non come parte di piano generata da una semiretta che ruota attorno all'origine) definizioni e teoremi in cui si fa riferimento ad angoli intesi come figure (ad es. la definizione di bisettrice di un angolo come asse di simmetria dei suoi lati, mentre gli angoli alla Choquet non hanno lati!).^*

* Nella sintesi storica non ci si è soffermati sulla caratterizzazione generale della geometria data nel 1872 da Klein: «dato un insieme S di elemnti (ad es. punti, rette, cerchi, …) e un gruppo G di trasformazioni applicate a S, la geometria associata a S e G è lo studio delle proprietà di S che rimangono invariate se a S sono applicate trasformazioni appartenenti a G». In questo modo venne precisato (e relativizzato) il significato di proprietà geometrica (se G è il gruppo dei movimenti abbiamo le proprietà metriche, se è il gruppo delle trasformazioni lineari abbiamo le proprietà affini, …

Q9  Per ottenere la figura B dalla figura A posso procedere nel modo illustrato a lato. Non è l'unico modo possibile. Si può anche procedere così: o così: o così:

    Queste sono i procedimenti che comportano la composizione del minor numero di trasformazioni.

    Il quesito, illustrando attività di costruzione geometrica al calcolatore mediante un semplice programma di tipo "paint" (cioè che realizza e memorizza i disegni come insiemi di pixel^*), mette in luce le opportunità didattiche che offre l'uso di una applicazione per fare disegni al calcolatore: che cosa fanno i vari comandi? a quali costruzioni e quali trasformazioni geometriche corrispondono? quali conoscenze geometriche (e in che forma) sono incorporate in una applicazione di questo tipo? …

* a differenza dei programmi di tipo "draw" (o "vettoriale"), che possono memorizzare separatamente le componenti di un disegno, registrare un segmento come coppia di punti, un poligono come successione finita di punti, …

    Sorgono, però, anche alcuni problemi, che, qui, ci limitiamo a enunciare (rinviando la loro discussione a uno specifico articolo sull'uso del calcolatore nell'ambito dell'insegnamento della geometria): 
•    l'uso del calcolatore quando, fino a che punto, … può sostituire l'uso di carta, matita, strumenti da disegno tradizionali?
•    l'impostazione dell'insegnamento della geometria dovrebbe essere rivisto anche alla luce delle caratteristiche del software grafico "vero" (quello che si usa nelle attività di disegno al calcolatore, sia amatoriali che didattiche o professionali), che ha strumenti diversi rispetto a compasso, riga, squadra, … tradizionali?
•    l'uso di software didattico (come "Cabri" e altri) che utilizza il calcolatore per fare costruzioni geometriche con linguaggio e strumenti "euclidei" trova una buona accettazione da parte di insegnanti che, invece, hanno difficoltà di fronte alle applicazioni grafiche standard: ciò è indice dell'efficacia di questo software o è la spia di un ulteriore tentativo, più o meno esplicito, più o meno consapevole, della scuola (e dell'insegnamento della matematica, in particolare) per "digerire" il nuovo (nella tecnologia, nelle professioni, nelle comunicazioni, …) senza cambiamenti sostanziali? 
    Naturalmente l'uso del calcolatore in ambiti geometrici non si ferma a questi aspetti: basti pensare allo studio delle trasformazioni dei più vari tipi (affini, proiettive, topologiche, conformi, …), che nel calcolatore trova un supporto eccezionale per visualizzazioni, congettura e sperimentazione di proprietà, …, allo studio delle curve, al calcolo delle estensioni, … e allo studio di problemi mediante la simulazione. 
    Relativamente all'ultimo aspetto, si pensi alle attività didattiche che si possono realizzare mettendo a punto insieme agli alunni (nel triennio) programmi che simulino situazioni come quella presentata in Q1. Sotto sono riprodotte alcune immagini generate da un programma che simula il dispositivo di Q1 (con XY/AB=0.85).

L'asta AB ruota man mano di 0.1°; dopo l'immagine riportata a destra il programma si arresta segnalando un errore di fuori dominio: 58.2° è il troncamento ai decimi di grado dell'inclinazione massima che può raggiungere l'asta AB.

Q10  Nel discutere il quesito ci riferiremo alla griglia riprodotta nella prima parte dell'articolo (e terremo conto delle osservazioni dei partecipanti agli incontri di aggiornamento in cui si sono proposti i quesiti), anche se per problemi di spazio trascuremo alcuni aspetti (su cui il lettore-insegnante è comunque invitato a riflettere).

A.1-2, C.2    Nei programmi della scuola dell'obbligo e in quelli del biennio e, in parte, in quelli del triennio, sono presenti gli stessi temi e gli stessi argomenti, ma non emerge con sufficiente chiarezza quali debbano essere man mano i diversi livelli di formalizzazione rispetto al ciclo scolastico precedente.
    A noi pare che gli obiettivi che sarebbe importante raggiungere nella scuola media inferiore e privilegiare nelle verifiche iniziali e nel recupero nel biennio (all'inizio della prima classe o prima di affrontare specifici argomenti) siano più quelli di "atteggiamento cognitivo" e di capacità di "operare" consapevolmente con le conoscenze di base per risolvere problemi. Ad esempio: 
(a)    saper usare strumenti di misura (righello, goniometro, cilindro graduato, bilancia, …) per determinare estensioni (direttamente o misurando altre grandezze fisiche con cui esistano legami di proporzionalità), saper calcolare l'area di qualche figura "strana" usando quadrettature o mediante triangolarizzazioni, saper confrontare ad occhio l'ampiezza di angoli disegnati (prescindendo dalle dimensioni dei segmenti con cui sono sono stati rappresentati i lati), saper associare a una misurazione la corrispondente precisione, avere idea che la precisione sulle misure dirette influisce sulla precisione delle misure indirette, … più che saper recitare formule (dirette e inverse) per il calcolo di aree di figure standard, essere addestrati a risolvere problemi stereotipati con coni sovrapposti a cubi, …; 
(b)    saper usare strumenti da disegno (tracciare perpendicolari e parallele usando squadra e riga, …), sapersi organizzare il "foglio di lavoro" (dal problema della scelta delle unità sugli assi al problema del dove e quali figure disegnare per prime per ottenere una certa figura composta), saper schematizzare con figure astratte situazioni concrete, saper passare da una descrizione verbale di una figura al suo disegno e viceversa, … più che ripetere definizioni e saper identificare con disinvoltura figure o elementi di figure disposte in modi "standard"; 
(c)    saper costruire/interpretare riproduzioni in scala (utilizzando equazioni del tipo y=kx, non con le famigerate regolette ad hoc per le proporzioni), saper calcolare distanze inacessibili utilizzando similitudini, saper associare ombre a oggetti e altri trasformati a figure originali, … più che conoscere i termini "trasformazioni affini", "omotetie", … 
(d)    aver riflettuto (non genericamente) sulle differenze tra linguaggio comune e linguaggi specialistici, aver svolto (in contesti semplici, ma non banali) qualche attività di sperimentazione-congettura-verifica-dimostrazione, avere confidenza con il ricondurre problemi ad altri problemi (ricondurre problemi di tipo geometrico ad altri problemi di tipo geometrico – sono esempi in questo senso anche alcune delle attività considerate in (a) –, realizzare o interpretare rappresentazioni grafiche di relazioni tra grandezze, visualizzare geometricamente proprietà algebriche, …), … più che aver imparato cose del tipo «il punto è l'ente geometrico senza dimensioni», «non si deve parlare di triangoli uguali ma di triangoli congruenti perché in matematica due oggetti sono uguali solo se sono la stessa cosa», …

C.1    Per esemplificare i livelli più alti di formalizzazione e precisione linguistica, di generalizzazione, di riflessione "interna", … a cui si deve puntare nel biennio, possiamo citare: 
(a)    l'uso delle coordinate non solo per rappresentare graficamente dati e funzioni ma come modo di fare geometria,
(b)    il teorema di Pitagora non solo per risolvere problemi ma anche come cardine della metrica euclidea,
(c)    le trasformazioni geometriche presentate anche analiticamente e mettendo a fuoco il concetto di "invariante".

B.1-2    Rispetto ai "vecchi" programmi vi sono grosse novità, tutte più o meno riconducibili all'esigenza di raccordarsi ai programmi della scuola media (del 1979): l'introduzione della geometria analitica (i programmi del liceo scientifico prevedevano solamente l'impiego del sistema di riferimento cartesiano per il tracciamento del grafico di alcune funzioni) e delle trasformazioni geometriche, il rinvio a eventuali studi successivi di una presentazione assiomatica della geometria, il suggerimento di integrare metodi sintetici, metodi analitici, utilizzo di trasformazioni geometriche, … nelle definizioni e nelle dimostrazioni, e indicazioni metodologiche generali in cui si invitano gli insegnanti a dare rilievo alla matematizzazione, a definire itinerari didattici che riorganizzino e integrino gli argomenti delle varie aree matematiche.
    Vi sono, però, vari punti dei nuovi programmi (sia nell'elenco dei contenuti che nei successivi commenti) che sollevano perplessità (sia didattiche che culturali): 
(a)    l'aver aggiunto (rispetto alla versione PNI) dopo «piano cartesiano» la specificazione «: retta, parabola, iperbole equilatera» sembra consentire di ridurre la geometria analitica al grafico di qualche funzione invece che assumerla come modo di fare geometria; la mancanza delle similitudini e del Teorema di Talete nel programma debole compromette la messa a fuoco dei collegamenti tra approccio sintetico e approccio analitico (a meno che non si ricorra alle similitudini in senso prematematico); si parla di introduzione del piano cartesiano come "modello" del piano euclideo, ma il riferimento al concetto di "modello di un sistema di assiomi" è contraddittorio con la rinuncia a una presentazione assiomatica (a meno che non si intenda il piano cartesiano come "modello matematico" del concetto prematematico di piano euclideo); 
(b)    non è più presente (rispetto alla versione PNI) il cerchio tra gli esempi di geometria analitica mentre (sia come curva che come luogo geometrico) è tra gli esempi più semplici e più significativi; le funzioni trigonometriche sono limitate agli angoli convessi (e le rotazioni? e i radianti, indispensabili per l'uso delle funzioni trigonometriche dei linguaggi di programmazione? …) e non è presa in considerazione la funzione tangente (e il collegamento tra angoli e coefficienti angolari? …); non è citata la possibilità di introdurre il concetto di vettore e di impiegarlo per lo sviluppo della geometria; 
(c)    per la geometria, dalla finalità di «descrivere e studiare razionalmente uno spazio» (PNI) si sia passati alla visione come «guida privilegiata alla consapevolezza argomentativa» (Brocca): il rilievo si è spostato dalla "matematizzazione" alla "argomentazione", lasciando intendere che le altre aree matematiche offrano/richiedano meno spazio per il ragionamento, trascurando le difficoltà specifiche delle dimostrazioni geometriche (le ipotesi implicite aggiunte illustrando il teorema con una figura particolare, la difficoltà di separare intuizione "fisica" e argomentazione "formale", …, di cui si è discusso esaminando i quesiti), non tenendo conto che il contesto delle attività di manipolazione algebrica (trasformare un termine o un'equazione attraverso passaggi successivi, applicando opportune proprietà) è forse più adatto per comprendere l'articolazione delle dimostrazioni, …

D, E    Affronteremo gli ultimi punti della griglia illustrando l'impostazione che abbiamo dato all'insegnamento della geometria nel progetto che stiamo costruendo.^*

* Al materiale didattico che stiamo elaborando abbiamo deciso di dare veste editoriale affinché gli insegnanti che lo sperimentano possano adottarlo come testo, liberando la sperimentazione dal condizionamento di libri di testo con impostazione divergente. Vedi il punto [9] della bibliografia.

    Per definire questa impostazione, un paio d'anni fa, ci siamo posti alcuni problemi:

(a)    In accordo con quanto indicato dai nuovi programmi, ritenevamo non proponibile una definizione assiomatica del piano (o dello spazio) euclideo, proprio per le difficoltà didattiche e concettuali esaminate in questo articolo discutendo i precedenti quesiti. Nello stesso tempo ci sembrava necessario, nella scuola secondaria superiore, dare una presentazione matematica, non solo sperimentale (nel senso "fisico" del termine), della geometria, sia per fornire una visione più esplicita e precisa della natura della matematica, sia per inquadrare meglio il significato delle dimostrazioni. 
(b)    L'impostazione dell'"Enriques-Amaldi" sembrava risolvere, almeno parzialmente, (a): la geometria non viene presentata come una "definizione assiomatica" di uno spazio astratto (non abbiamo capitoli introduttivi che, come nel caso del libro del quesito 4, tentano di spiegare quanto asserito da Hilbert nella sua premessa agli assiomi), ma il modo in cui vengono man mano introdotti gli assiomi e svolte le dimostrazioni (traendo spunti, facendo confronti, mettendo a fuoco le approssimazioni, evidenziando le "economie" di ragionamento, … rispetto a verifiche e costruzioni "sperimentali") mirano piuttosto a far percepire la natura e gli scopi di una organizzazione razionale delle conoscenze, a educare all'uso del linguaggio e del ragionamento, … . Ma non ci soddisfaceva il riferimento, troppo ristretto, allo spazio della "fisica" e, soprattutto, non ci sembrava che questi obiettivi educativi oggi (a quasi un secolo dall'ideazione dell'impostazione di tale libro), di fronte agli enormi sviluppi che ha avuto la matematica e alle molte forme attraverso cui essa si è diffusa nelle professioni e nella vita di tutti i giorni, potessero essere raggiunti attraverso una così estesa e "isolata" trattazione della geometria euclidea. 
(c)    Un ultima questione era costituita dalle indicazioni contenutistiche dei nuovi programmi: l'introduzione di nuovi argomenti era in accordo con le considerazioni finali del precedente punto (b), ma l'assenza di altri argomenti (di cui abbiamo discusso nelle pagine precedenti) sembrava pregiudicare la possibilità di una adeguata presentazione "matematica" della geometria. Abbiamo risolto questo problema interpretando queste "assenze" nel modo che ci sembra più naturale: non come dei suggerimenti a non affrontare gli argomenti non citati, ma come un modo di cautelarsi da una loro presentazione sistematica, formalizzata, macchinosa, con classificazioni in casi e sottocasi, … (come avviene in genere nelle implementazioni editoriali dei programmi scolastici), sottointendendo che, se si trovano dei naturali intrecci con altri concetti previsti dai programmi e se non sono necessari particolari prerequisiti, questi argomenti possono essere affrontati, lasciando ai livelli scolastici successivi una loro maggiore formalizzazione.

    Abbiamo, quindi, scelto un'impostazione che possiamo sintetizzare così (rinviando ai volumi del progetto e alla relativa guida per una descrizione dettagliata): 
•   Introduzione di alcuni concetti geometrici per via analitica (dopo aver introdotto la struttura dei numeri reali costruttivamente, come numeri decimali illimitati dotati di una opportuna nozione di eguaglianza e di opportune operazioni, definite algoritmicamente). Riferendosi al piano: • punto come coppia di numeri reali, • figura come insieme di punti, • traslazione come particolare funzione numerica a 2 input e 2 output, • distanza come opportuna funzione numerica a 4 input 1 output, • direzione come elemento dell'intervallo [0,360), … 
•   Introduzione di altri concetti, trattazione di problemi e dimostrazioni, … a volte analiticamente, a volte sinteticamente (ad esempio una semiretta, invece che analiticamente, mediante un sistema equazione+disequazione, può essere descritta come l'insieme di punti in cui un punto dato può essere trasformato mediante traslazioni di direzione fissata). 
•   Questi concetti vengono introdotti man mano come modelli matematici che astraggono e generalizzano concetti "fisici" (dalle posizioni su righe e su superfici individuate con strumenti di misura ai punti come n-uple di numeri, dalle direzioni scandite da un goniometro alla associazione di un intervallo [a,b) ai punti del cerchio x²+y²=1, …), dopo lo svolgimento di riflessioni e attività operative (con strumenti da disegno e di misura) in situazioni "concrete". 
•   In particolare il piano euclideo è introdotto come R² dotato della distanza euclidea, ma si considerano anche altre distanze (in particolare la distanza urbanistica). E si considerano anche altri spazi, di tipo fisico (gli spazi mono e tridimensionali, la geometria della sfera, la geometria dell'indice grafico dell'orario ferroviario, …) e no (i grafi per rappresentare relazioni tra oggetti, …).

Indicazioni bibliografiche

–    Riferimenti "tecnici": [2], [12], [10], [8], [3], [4]. 
–    Riferimenti "storico-epistemologici": [11], [8], [1], [10] (l'introduzione di Manara), [13], [14]; per altre indicazioni bibliografiche vedi [5]. 
–    Riferimenti "didattici": [5] - [7], [9], [15].

[1]	Israel G. - Lomabrdo Radice L. - Taton R. e altri, Storia della scienza - vol. II, Laterza, Bari, 1976
[2]	Accascina G. - Villani V., Geometria, ETS, Pisa, 1983
[3]	Blumenthal L., A modern view of Geometry, Freeman, S.Francisco, 1961
[4]	Choquet G., L'enseignement de la géométrie, Hermann, Paris, 1964
[5]	Dapueto C., La problematica del definire e del dimostrare nella costruzione di un progetto per l'insegnamento della matematica, in: F.Furinghetti (a cura di), Atti del 2° internucleo scuola secondaria superiore, Progetto T.I.D.-Formazione e aggiornamento in matematica degli insegnanti, quaderno 13, 1992
[6]	– (a cura di), MaCoSa, vol. 1 - Guida per gli insegnanti, Rapporto Tecnico, Dipartimento di Matematica dell'Università, Genova, 1994
[7]	– , Relazione del gruppo di lavoro "L'impostazione dell'insegnamento della geometria nella scuola secondaria superiore", in: Atti del XVII Convegno dell'U.M.I. sull'Insegnamento della Matematica (Latina, ottobre 1994)
[8]	Enriques F. (a cura di), Questioni riguardanti le matematiche elementari, Zanichelli, Bologna, 1924-1927
[9]	Gruppo didattico MaCoSa, MaCoSa: Matematica per Conoscere e per Sapere, vol. 1, Casa Editrice Maggi, Ceranesi, 1994
[10]	Hilbert D., Fondamenti della Geometria, Feltrinelli, Milano, 1970
[11]	Lolli G., Capire una dimostrazione, Il Mulino, Bologna, 1988
[12]	Moise E.E., Elementary Geometry from an advanced standpoint, Addison-Wesley, Reading, 1963
[13]	Rota G.C., Matematica e filosofia: storia di un malinteso, B.U.M.I., 7, 1990
[14]	Russell B., Storia della filosofia occidentale, Longanesi, Milano, 1966
[15]	Zeitler H., Axiomatics of Geometry in School and in Science, For the Learning of Mathematics, vol. 10, 1990

Appendice 1: dagli Elementi di Euclide

Definizioni (Def)   [estratto: in tutto sono 23] 

1	Un PUNTO è ciò che non ha parti
2	Una LINEA è lunghezza senza larghezza
3	Le estremità di una linea sono punti
4	Una LINEA RETTA è una linea che giace uniformemente rispetto ai suoi punti
5	Una SUPERFICIE è ciò che ha soltanto lunghezza e larghezza
6	Le estremità di una superficie sono linee
7	Una SUPERFICIE PIANA è una superficie che giace uniformemente rispetto alle linee rette su di essa
8	Un ANGOLO PIANO è l'inclinazione reciproca di due linee in un piano che si incontrano e non giacciono in linea retta
13	Un CONTORNO è ciò che è all'estremità di ogni cosa
14	Una FIGURA è ciò che è contenuto da qualche contorno
15	Un CERCHIO è una figura piana contenuta da una linea tale che tutte le linee rette che la incontrano da un punto fra quelli che giacciono dentro la figura sono uguali l'una con l'altra
16	E quel punto è detto il CENTRO del cerchio
19	FIGURE rettilinee sono quelle che sono contenute da linee rette, TRILATERE quelle contenute da tre, QUADRILATERE quelle contenute da quattro e MULTILATERE quelle contenute da più di quattro
20	Delle figure trilatere, un TRIANGOLO EQUILATERO è quella che ha tre lati uguali, un TRIANGOLO ISOSCELE quella che ha soltanto due dei suoi lati uguali, e un TRIANGOLO SCALENO quella che ha i suoi tre lati ineguali.

Nozioni comuni (Nc)   [estratto: in tutto sono 8]

1	Cose che sono uguali a una stessa cosa sono anche uguali fra loro
3	Se uguali sono sottratti da uguali, i rimanenti sono uguali
7	Cose che coincidono l'una con l'altra sono uguali fra loro

Postulati (Post) 

1	Si tracci una linea retta da un punto qualsiasi a un punto qualsiasi
2	Si prolunghi una linea retta terminata con continuità su una linea retta
3	Si descriva un cerchio con qualunque centro e distanza
4	Tutti gli angoli retti siano uguali fra loro
5	Se una linea retta incontrando due linee rette forma da una stessa parte angoli interni minori di due retti, le due linee rette, se prolungate indefinitamente, si incontrino dalla parte in cui vi sono gli angoli minori di due retti

Proposizione 1
Su una data retta finita, costruire un triangolo equilatero. 
Dim.: 
0)  Considero il segmento AB 
1)  Applico Post3 prendendo come centro il punto A e come raggio il segmento AB 
2)  Applico ancora Post3, considerando come centro B e raggio AB 
3)  Sia C uno dei due punti di intersezione fra le due circonferenze che ho costruito. Applico Post1 scegliendo come punti A e C 
4)  Applico ancora Post1, scegliendo come punti B e C  5)  Per Def15 si ha: AC = AB 
6)  Per Def15 si ha: BC = AB 
7)  Da 6) e 7) e da Nc6 ottengo: AC = BC 
8)  Da 5), 6) e 7) e da Def20 ottengo che ABC è un triangolo equilatero.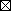    

Proposizione 2
Costruire da un punto dato una linea retta uguale ad una linea retta data.
Dim.: [omissis]    

Proposizione 4
Se due triangoli hanno due lati uguali a due lati rispettivamente e hanno uguali gli angoli contenuti dalle linee rette uguali, essi avranno anche la base uguale alla base, il triangolo sarà uguale al triangolo, e gli angoli rimanenti saranno uguali rispettivamente agli angoli rimanenti, e precisamente quelli che sono sottesi dai lati uguali

Dim : 0)  Considero i due triangoli ABC e DEF. Sia: AB=DE, AC=DF, ∠A=∠D 1)  Trasporto il primo triangolo sul secondo in modo che il punto A si sovrapponga a D e il segmento AB si disponga lungo DE 2)  Poiché AB=DE, per 1) risulta che B è sovrapposto a E e AB è sovrapposto a DE
3)  Poiché ∠A=∠D e, per 1), AB è disposto lungo DE, si ha che AC è disposto lungo DF 4)  Poiché AC=DF e, per 1), A è sovrapposto a D, da 3) risulta che C è sovrapposto a F e che AC è sovrapposto a DF 5)  Poiché per 2) e 4) B e C sono rispettivamente sovrapposti a E e F si ha che BC è sovrapposto ad EF 6)  Quindi per Nc7, da 2), 4) e 5) segue che i triangoli ABC e DEF sono uguali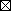

Appendice 2: dai Fondamenti della geometria di Hilbert
    [estratto con i soli assiomi relativi alla geometria piana]